DC Pandey Solutions: Mechanics of Rotational Motion - 2 | DC Pandey Solutions for JEE Physics PDF Download
Introductory Exercise 9.4
Ques 1: A thin circular ring of mass M and radius R is rotating about its axis with an angular speed ω0. Two particles each of mass m are now attached at diametrically opposite points. Find the new angular speed of the ring.
Ans: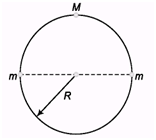
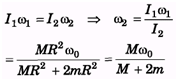
Ques 2: If the ice at the poles melts and flows towards the equator, how will it affect the duration of day-night ?
Ans: As ice melts at pole and flows to equator, it gets distributed away from centre (as equitorial radius is greater than polar radius) such that moment of inertia about axis increases which results in decrease in angular speed (as Iω= constant), this leads in increase in time period 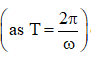 or duration of day and night.
or duration of day and night.
Introductory Exercise 9.5
Ques 1: In sample example 9.16, find the equation y(x)if at the initial moment the axis c of the disc was located at the point O after which it moved with a constant linear acceleration a0 (and the zero initial velocity) while the disc rotates counter clockwise with a constant angular velocity w.
Ans: 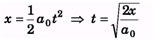
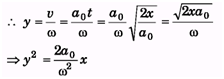
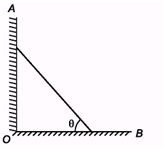
Ques 2. A uniform bar of length l stands vertically touching a wall OA. When slightly displaced, its lower end begins to slide along the floor. Obtain an expression for the angular velocity w of the bar as a function of q. Neglect friction everywhere.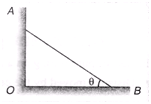
Ans: 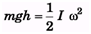
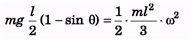
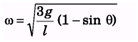
Introductory Exercise 9.6
Ques 1: A solid sphere of mass m rolls down an inclined plane a height h. Find rotational kinetic energy of the sphere. [Hint: Mechanical energy will remain conserved]
Ans: 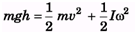
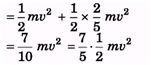
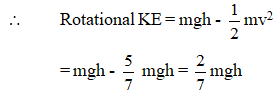
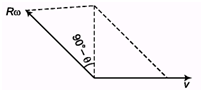
Ques 2: A ring of radius R rolls on a horizontal ground with linear speed v and angular speed ω. For what value of 8 the velocity of point P is in vertical direction, (v < R ω)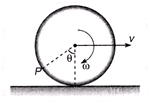
Ans;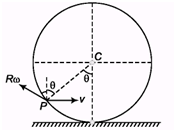
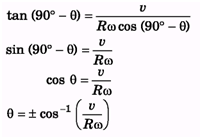
Ques 3: The topmost and bottommost velocities of a disc are v1 and v2 (< v1) in the same direction. The radius is R. Find the value of angular velocity ω.
Ans: 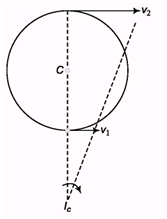
ωx = v1 and ω (x + 2R) = v2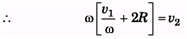
2Rω = v2 - v1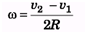
Introductory Exercise 9.7
Ques 1. A ball of mass M and radius R is released on a rough inclined plane of inclination q. Friction is not sufficient to prevent slipping. The coefficient of friction between the ball and the plane is m. Find:
(a) the linear acceleration of the ball down the plane,
(b) the angular acceleration of the ball about its centre of mass.
Ans: 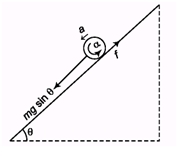
f = f2 = mN = mmg cos θ
(a) ma = mg sin θ - m mg cos θ
a = g (sin θ - m cos θ)
(b) Rf = Iα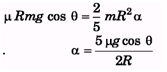
Ques 2. Work done by friction in pure rolling is always zero. Is this statement true or false?
Ans: Work done by friction is zero only in uniform pure rolling but not in accelerated pure rolling. So, the statement is false.
Ques 3. A spool is pulled by a force in vertical direction as shown in figure.
What is the direction of friction in this case? The spool does not loose contact with the ground.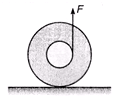
Ans: 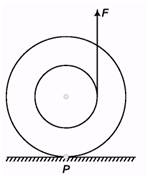
As the torque due to applied force is anti-clockwise, so the point of contact tries to slip rightwards and friction tries to prevent it and so acts leftwards.
Ques 4. A cylinder is rolling down a rough inclined plane. Its angular momentum about the point of contact remains constant. Is this statement true or false?
Ans: As during rolling down, friction acts upward which exerts a torque, thus the angular momentum of the system is not conserved. Even if we take axis of rotation at point of contact, then component of weight exerts torque, so, statement is false.
Ques 5. Two forces F1 and F2 are applied on a spool of mass M and moment of inertia I about an axis passing through its centre of mass. Find the ratio F1/F2 , so that the force of friction is zero. Given that I < 2Mr2.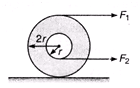
Ans: Force of friction will be zero, only when there is uniform pure rolling, i.e., there is no external unbalanced torque.
Thus, a = Rα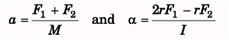
as, a = 2rα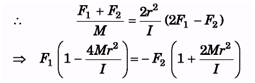
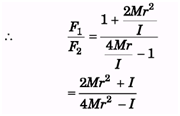
Ques 6. A disc is placed on the ground. Friction coefficient is m. What is the minimum force required to move the disc if it is applied at the topmost point?
Ans: 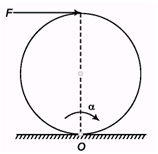
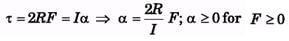
i.e., even a slightest amount of force can initiate motion of the disk.
Ques 7. When a body rolls, on a stationary ground, the acceleration of the point of contact is always zero. Is this statement true or false?
Ans: Acceleration of point of contact is zero only when there is uniform pure rolling and no slipping
Introductory Exercise 9.8
Ques 1: A cube is resting on an inclined plane. If the angle of inclination is gradually increased, what must be the coefficient of friction between the cube and plane so that,
(a) cube slides before toppling?
(b) cube topples before sliding?
Ans: 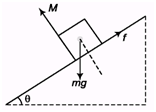
For sliding,
mg sin θ > μ mg cos θ
∴ tan θ > μ
And for toppling,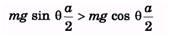
∴ tan θ > 1
(a) Cube will slide before toppling if tan θ < 1, i.e., μ < 1 and
(b) Cube will topple before sliding if tan θ > 1, i.e., μ > 1
Ques 2: A solid sphere of mass M and radius R is hit by a cue at a height h above the centre C. For what value of h the sphere will roll without slipping?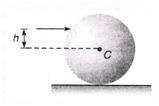
Ans: 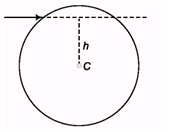
For rolling without slipping on horizontal plane, f = 0
Impulse, Im = Δp = mv Angular Impulse, Imh = ΔL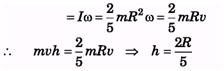
FAQs on DC Pandey Solutions: Mechanics of Rotational Motion - 2 - DC Pandey Solutions for JEE Physics
| 1. What are the basic principles of rotational motion? |  |
| 2. How is rotational motion different from linear motion? |  |
| 3. How is torque related to rotational motion? |  |
| 4. What is the significance of moment of inertia in rotational motion? |  |
| 5. How can angular velocity and angular acceleration be calculated in rotational motion? |  |
















