Motion Class 9 Notes Science Chapter 7
In our daily lives, objects such as birds, fish, and cars can be either at rest or in motion. Motion is observed when an object's position changes over time. Sometimes, motion is inferred indirectly, like noticing dust moving to deduce air movement. Perception of motion can vary: passengers in a moving bus see trees moving backward, while onlookers outside the bus see both the bus and its passengers in motion.
 Motion
Motion
Describing Motion
To describe an object's motion, we use a reference point, or origin, as a fixed location. For instance, if a school is 2 km north of a railway station, the railway station is the reference point. This origin helps us measure and describe the object's position relative to it.
What is Motion?
A body is said to be in a state of motion when its position changes continuously with reference to a point. Motion can be of different types depending upon the type of path by which the object is travelling through:
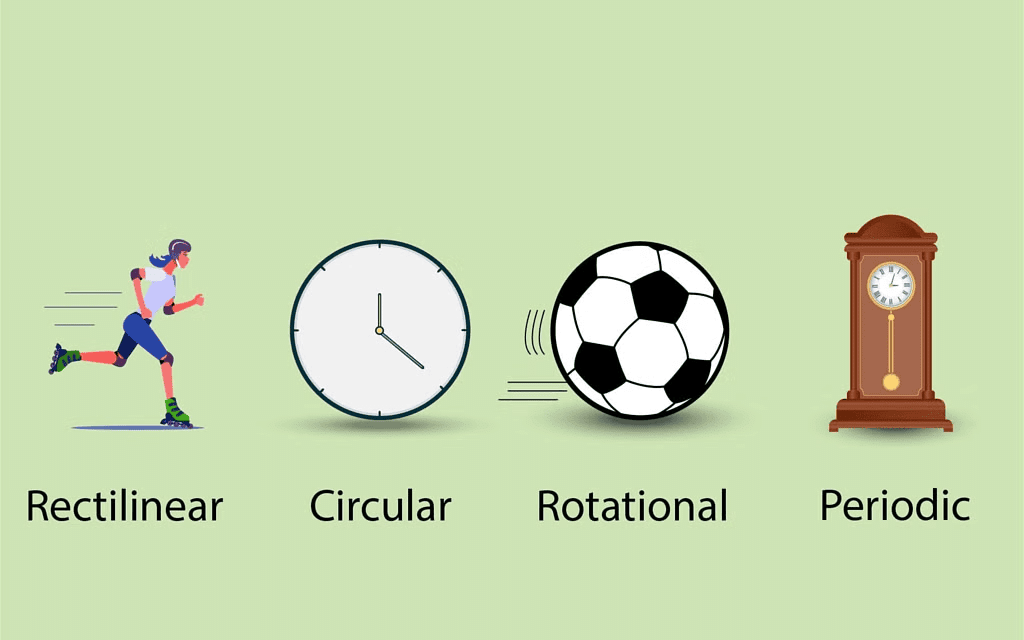 Types of Motion
Types of Motion
- Circulatory motion/Circular motion: In a circular path.
- Linear motion: In a straight-line path.
- Oscillatory/Vibratory motion: To and fro path with respect to origin.
Motion Along a Straight Line
The simplest type of motion is along a straight line.
Let's understand this with an example. Imagine an object moving along a straight path, starting from point O, which we use as the reference point.
 Motion along a straight line
Motion along a straight line
Example Description
- Initial Motion: The object starts at point O and moves to point A via points C and B.
- Return Motion: The object then travels back from A to C through B.
Distance Covered
The total path length covered by the object is the sum of the distances traveled:
- Distance from O to A: 60 km
- Distance from A to C: 35 km
- Total Distance from O to C = OA + AC = 60 km + 35 km = 95 km
Distance is a scalar quantity, meaning it only has magnitude and no direction.
- Scalar quantity: It is the physical quantity having its own magnitude but no direction.
Example: Distance, Speed. - Vector quantity: It is the physical quantity that requires both magnitude and direction.
Example: Displacement, Velocity.
Distance and Displacement
1. Distance
The actual path of length travelled by an object during its journey from its initial position to its final position is called the distance.
- Distance is a scalar quantity that requires only magnitude but no direction to explain it.
- Example: Ramesh travelled 65 km. (Distance is measured by odometer in vehicles.)
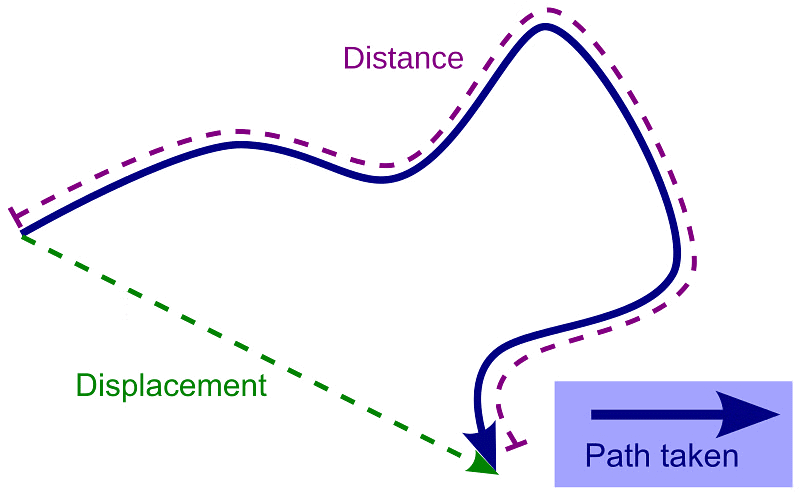
2. Displacement
The shortest distance travelled by an object during its journey from its initial position to its final position is called displacement.
- Displacement is a vector quantity requiring both magnitude and direction for its explanation.
- Example: Ramesh travelled 65 km southwest from Clock Tower.
- Displacement can be zero (when the initial point and final point of motion are the same)
Example: Circular motion.
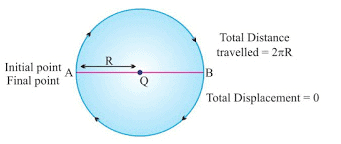 Example of Zero Displacement
Example of Zero Displacement
Example 1: A body travels in a semicircular path of radius 10 m starting its motion from point ‘A’ to point ‘B’. Calculate the distance and displacement.
Sol. Given, π = 3.14, R = 10 m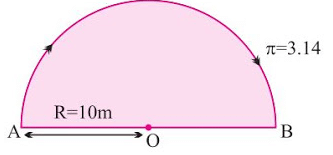
The distance is the length of the semicircular path.
Distance = Circumference of a circle ÷ 2
Distance = 2πR ÷ 2
Distance = πR
= 3.14 × 10 = 31.4 m
Where as ,
Displacement = 2 × R = 2 × 10 = 20 m
Example 2: A body travels 4 km towards North then he turns to his right and travels another 4 km before coming to rest. Calculate
(i) total distance travelled,
(ii) total displacement.
Sol. The total distance is the sum of all the paths travelled:
Total Distance = 4km (North) + 4km (Right) = 8km
Since displacement is the shortest straight-line distance between the starting point and the final point.
The path forms a right triangle, where:
- One leg = 4 km (North direction),
- Other leg = 4 km (Right direction).
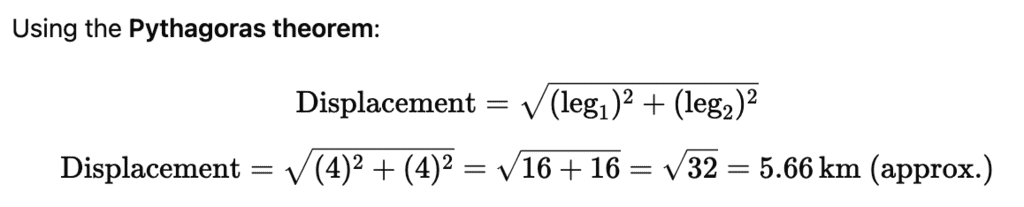
Uniform and Non-uniform Motion
1. Uniform Motion
- When a body travels equal distances in equal intervals of time, then the motion is said to be a uniform motion.
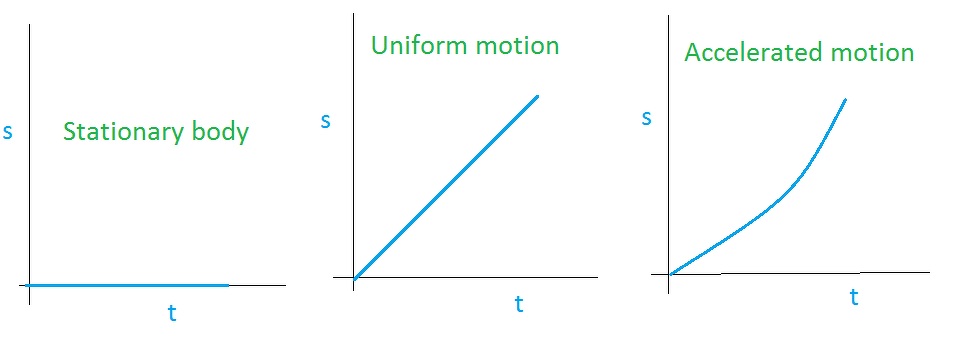
2. Non-uniform Motion
- In this type of motion, the body travels unequal distances in equal intervals of time.
- Two types of non-uniform motion:
(i) Accelerated Motion: When the motion of a body increases with time.
(ii) De-accelerated Motion: When the motion of a body decreases with time.
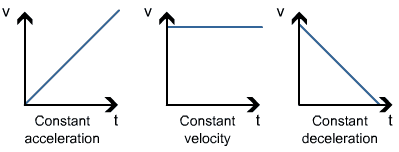
Measuring the Rate of Motion
The measurement of distance travelled by a body per unit of time is called speed.
i.e. Speed (v) = Distance Travelled/Time Taken = s/t
- SI unit: m/s (meters/second)
- If a body is executing uniform motion, then there will be a constant speed.
- If a body is travelling with a non-uniform motion, then the speed will not remain uniform but have different values throughout the motion of such a body.
- For non-uniform motion, the average speed will describe one single value of speed throughout the motion of the body.
i.e. Average speed = Total distance travelled/Total time taken
Conversion Factor
Change from km/hr to m/s = 1000m/(60×60)s = 5/18 m/s
Example: What will be the speed of body in m/s and km/hr if it travels 40 km in 5 hrs?
Sol: Distance (s) = 40 km
Time (t) = 5 hrs.
Speed (in km/hr) = Total distance/Total time = 40/5 = 8 km/hr
40 km = 40 × 1000 m = 40,000 m
5 hrs = 5 × 60 × 60 sec.
Speed (in m/s) = (40 × 1000)/(5×60 ×60) = 80/36 = 2.22 m/s
Speed with Direction
- It is the speed of a body in a given direction.
- The measurement of displacement travelled by a body per unit of time is called velocity.
i.e. Velocity = Displacement/Time - SI unit of velocity: ms-1
- Velocity is a vector quantity. Its value changes when either its magnitude or direction changes.
- It can be positive (+ve), negative (-ve) or zero.
- For non-uniform motion in a given line, average velocity will be calculated in the same way as done in average speed.
i.e. Average velocity = Total displacement/Total time - For uniformly changing velocity, the average velocity can be calculated as follows:-
Avg. Velocity (vavg) = (Initial velocity + Final velocity)/2 = (u+v)/2
where, u = initial velocity, v = final velocity
Example 1: During the first half of a journey by a body it travels with a speed of 40 km/hr and in the next half it travels at a speed of 20 km/hr. Calculate the average speed of the whole journey.
Sol: The average speed for a journey where the distances are equal but the speeds are different is not simply the arithmetic mean
When a body covers equal distances at different speeds, the correct formula for average speed is: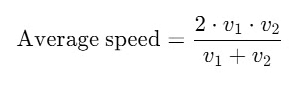 Given:
Given:
- Speed during the first half () = 40 km/hr
- Speed during the second half () = 20 km/hr
Now, use the correct formula: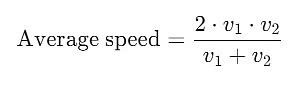
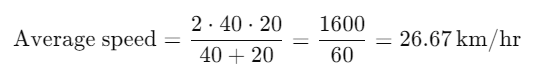
Example 2: A car travels 20 km in first hour, 40 km in second hour and 30 km in third hour. Calculate the average speed of the vehicle.
Sol: Speed in 1st hour = 20 km/hr
Distance travelled during 1st hr = 1 × 20= 20 km
Speed in 2nd hour = 40 km/hr
Distance travelled during 2nd hr = 1 × 40= 40 km
Speed in 3rd hour = 30 km/hr
Distance travelled during 3rd hr = 1 × 30= 30 km
Average speed = Total distance travelled/Total time taken
= (20 + 40 + 30)/3 = 90/3 = 30 km/hr
Rate of Change of Velocity
- Acceleration is seen in non-uniform motion and it can be defined as the rate of change of velocity with time.
i.e. Acceleration (a) = Change in velocity/Time = (v-u)/t
where, v = final velocity, u = initial velocity - Here, v > u, then ‘a’ will be positive (+ve). If v is greater than u, then acceleration (a) will be positive.
Example: A car speed increases from 40 km/hr to 60 km/hr in 5 sec. Calculate the acceleration of car.
Sol. u = 40km/hr = (40×5)/18 = 100/9 = 11.11 m/s
v = 60 km/hr = (60×5)/18 = 150/9 = 16.66 m/s
t = 5 sec
a = (v-u)/t = (16.66 - 11.11)/5 = 5.55/5 = 1.11 ms-2
Retardation/Deceleration
- Deceleration is seen in non-uniform motion during decrease in velocity with time. It has same definition as acceleration.
i.e. Deceleration (a') = Change in velocity/Time = (v-u)/t - Here, v < u, ‘a’ = negative (-ve).
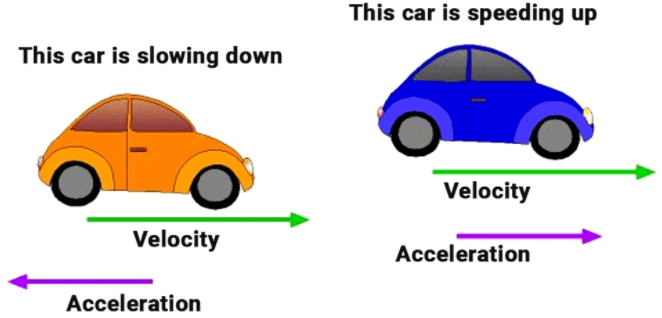
Example: A car travelling with a speed of 20 km/hr comes into rest in 0.5 hrs. What will be the value of its retardation?
Sol. v = 0 km/hr, u = 20 km/hr, t = 0.5 hrs
Retardation, a = (v-u)/t = (0-20)/0.5 = -200/5 = -40 km hr-2
Watch the animated video below to understand the concepts in an easy manner.
Graphical Representation of Motion
1. Distance-Time Graph (s/t graph)
(i) s/t graph for uniform motion: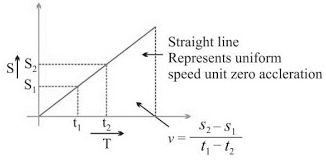 (ii) s/t graph for non-uniform motion:
(ii) s/t graph for non-uniform motion: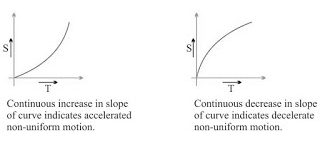
(iii) s/t graph for a body at rest: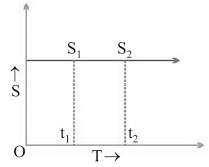 v = (s2 - s1)/(t2 - t1)
v = (s2 - s1)/(t2 - t1)
But, s2 - s1
∴ v = 0/(t2 - t1) or v = 0
2. Velocity-Time Graph (v/t graph)
(i) v/t graph for uniform motion: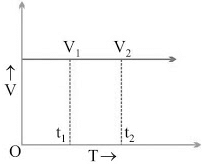 a = (v2 - v1)/(t2 - t1)
a = (v2 - v1)/(t2 - t1)
But, v2 - v1
∴ a = 0/(t2 - t1) or a = 0
(ii) v/t graph for uniformly accelerated motion: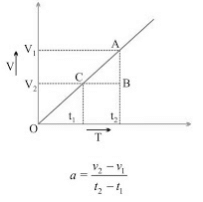 In uniformly accelerated motion, there will be an equal increase in velocity in equal intervals of time throughout the motion of the body.
In uniformly accelerated motion, there will be an equal increase in velocity in equal intervals of time throughout the motion of the body.
(iii) v/t graph for non-uniformly accelerated motion: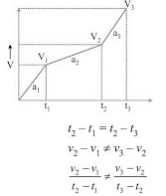 a2 ≠ a1
a2 ≠ a1
(iv) v/t graph for uniformly decelerated motion: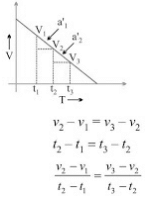 a1' = a2'
a1' = a2'
(v) v/t graph for non-uniformly decelerated motion: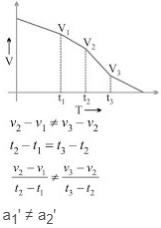
Note: In v/t graph, the area enclosed between any two time intervals, t2 - t1, will represent the total displacement by that body.
The displacement can also be calculated as the area of the trapezium formed by the v/t graph:
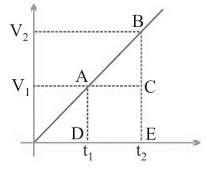
= Area of ∆ABC + Area of rectangle ACDB = ½ × (v2 – v1)×(t2 - t1) + v1× (t2 - t1)
Example: From the information given in the s/t graph, which of the following body ‘A’ or ‘B’ will be faster?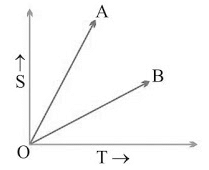 Sol. vA > vB
Sol. vA > vB
Equations of Motion by Graphical Method
1. First Equation: v = u + at
Final velocity = Initial velocity + Acceleration × Time
Graphical Derivation
Suppose a body has initial velocity ‘u’ (i.e., velocity at time t = 0 sec.) at point ‘A’ and this velocity changes to ‘v’ at point ‘B’ in ‘t’ secs. i.e., final velocity will be ‘v’.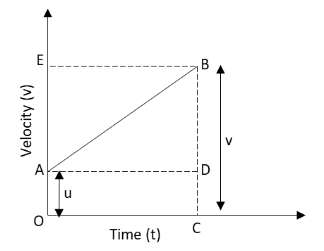
For such a body there will be an acceleration. a = Change in velocity/Change in Time
⇒ a = (OB - OA)/(OC-0) = (v-u)/(t-0)
⇒ a = (v-u)/t
⇒ v = u + at
2. Second Equation: s = ut + ½ at2
Distance travelled by object = Area of OABC (trapezium)
= Area of OADC (rectangle) + Area of ∆ABD
= OA × AD + ½ × AD × BD
= u × t + ½ × t × (v – u)
= ut + ½ × t × at
⇒ s = ut + ½ at2 (∵a = (v-u)/t)
3. Third Equation: v2 = u2 + 2as
s = Area of trapezium OABC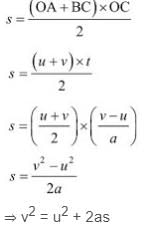
Example 1: A car starting from rest moves with a uniform acceleration of 0.1 ms-2 for 4 mins. Find the speed and distance travelled.
Sol: u = 0 ms-1 (∵ car is at rest), a = 0.1 ms-2, t = 4 × 60 = 240 sec.
v = ?
From, v = u + at
v = 0 + (0.1 × 240) = 24 ms-1
Example 2: The brakes applied to a car produces a deceleration of 6 ms -2 in the opposite direction to the motion. If a car requires 2 sec. to stop after the application of brakes, calculate the distance travelled by the car during this time.
Sol: Deceleration, a = − 6 ms-2; Time, t = 2 sec.
Distance, s =?
Final velocity, v = 0 ms-1 (∵ car comes to rest)
Now, v = u + at
⇒ u = v – at = 0 – (-6×2) = 12 ms-1
s = ut + ½ at2 = 12 × 2 + ½ (-6 × 22) = 24 – 12 = 12 m
Uniform Circular Motion
- If a body is moving in a circular path with uniform speed, then it is said to be executing the uniform circular motion.
- In such a motion the speed may be the same throughout the motion but its velocity (which is tangential) is different at each and every point of its motion. Thus, uniform circular motion is an accelerated motion.
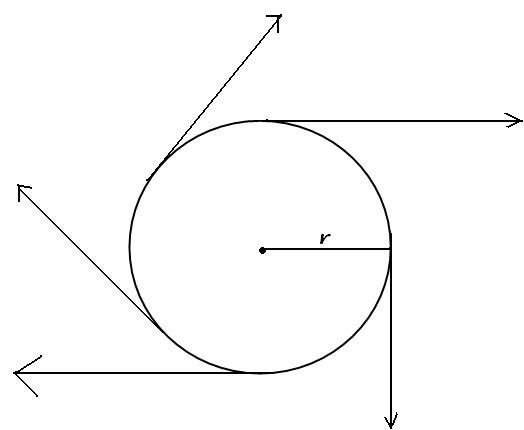 Direction at different points while executing circular motion
Direction at different points while executing circular motion

|
84 videos|478 docs|60 tests
|
FAQs on Motion Class 9 Notes Science Chapter 7
| 1. What is the difference between distance and displacement? |  |
| 2. How do you calculate average speed? |  |
| 3. What is retardation or deceleration? |  |
| 4. How can motion be represented graphically? |  |
| 5. What are the equations of motion, and how can they be derived using graphs? |  |