Difficult Units Digits Questions | Quantitative Reasoning for GRE PDF Download
First, a couple 800+ practice questions (yes, you read that right – 800+) on which to whet your chops.
1) The units digit of 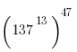 is :
is :
(A) 1
(B) 3
(C) 5
(D) 7
(E) 9
2) The units digit of 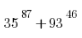 is:
is:
(A) 2
(B) 4
(C) 6
(D) 8
(E) 0
3) The units digit of 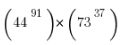
(A) 2
(B) 4
(C) 6
(D) 8
(E) 0
Admittedly, these problems are probably a notch harder than anything you are likely to see on the GMAT. If you understand these, you definitely will understand anything of this variety that the GMAT throws at you!
Not what it seems
All of those problems above involve numbers with hundreds of decimal places. No one can calculate those answers without a calculator: in fact, no calculator would be sufficient to do the calculation, because no calculator can accommodate that many digits. If one needed the exact answer, one could always use that most extraordinary web computing tool, Wolfram Alpha. Of course, one will not have access to the web or a calculator or anything other than one’s owns wits when confronting a question such as this on the GMAT. How do we proceed?
It turns out, what appears as a ridiculously hard calculation is actually quite easier. No part of the calculation we are going to do will involve anything beyond single-digit arithmetic!
Units digit arithmetic
The units digits of large numbers are special: they form a kind of elite and exclusive club. The big idea: only units digits affect units digits. What do I mean by that? Well, first of all, suppose you add or subtract two large numbers —- the units digit of the sum or the difference will depend only on the units digits of the two input numbers. For example, 3 + 5 = 8 —- this means that any number ending in 3 plus any number ending in 5 will be a number ending in 8. If you remember your “column addition” processes from grade school, this one might make intuitive sense.
The one that can be a little harder for folks to swallow is multiplication. If you multiply two large numbers, the unit digit of the product will have the same units digit as the product of the units digit of the two factors. That’s a mouthful! In other words, let’s take 3*7 = 21, so a units digit of a 3, times a unit digit of a 7, equals a units digit of a 1. That means, we could take any large number ending in 3, times any large number ending in 7, and the product absolutely will have to have a units digit of 1. If this is new idea to you, I strongly recommend: sit down with a calculator and multiply ridiculously large numbers together, with all combinations of units digits, until you are 100% satisfied that this pattern works.
Units digits and powers
This part will be a recap of an earlier post on powers of units digits. When we raise to a power, of course, that’s iterated multiplication, so we just follow the multiplication rule above. As it turns out, a simple pattern will always emerge.
Suppose we were considering powers of 253 — first of all, only the units digit, 3, matters, for the units digit of the powers. Any number ending in three will have the same sequence of units digits for the powers.
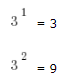
9*3 = 27, so 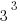 has a units digit of 7
has a units digit of 7
7*3 = 21, so 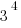 has a units digit of 1
has a units digit of 1
1*3 = 3, so 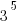 has a units digit of 3
has a units digit of 3
3*3 = 9, so 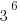 has a units digit of 9
has a units digit of 9
9*3 = 27, so 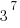 has a units digit of 7
has a units digit of 7
7*3 = 21, so 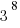 has a units digit of 1
has a units digit of 1
Notice a pattern has emerged — 3, 9, 7, 1, 3, 9, 7, 1, 3, 9, 7, 1, … It repeats like mathematical wallpaper. The pattern has a period of 4 — that is to say, it take four steps to repeat. This means, 3 to the power of any multiple of 4 has a units digit of 1: 38,356 and 3444 and all have a units digit of one. If I want to find power that’s not a multiple of 4, that’ easy: I just go to the nearest multiple of 4 and follow the wallpaper from there. For example, if I wanted 3446 —–
3444 has a units digit of 1
3445 has a units digit of 3
3446 has a units digit of 9
As it happens, 3446 is a number that has 213 digits, but the units digit must be a 9. The really expansive idea: everything I have just said about powers of 3 also applies to any larger number that happens to have a units digit of 3. Thus,
253446 has a units digit of 9.
That number has over a thousand digits (you don’t need to know how to figure that out!) but we know for sure that the units digit of this gargantuan number is 9.
Summary
Finally, on a totally gratuitous note, here, in it’s the full thousand-plus-digit glory, is 253446, courtesy of Wolfram Alpha:
253446 = 6190880832531899190821690500833264378796558621138440416684569816896956548548008694
5501637120599244459832600741641042834529231770919235178215551804306285786976623543
72380800482154741117883167160446214356675850891464689434900627878445424968534812213
04515041521698298553935861735825956938171070649017829532068323699186643091574519875
641384511684642401730622089635116285314952964987090639595147866795944410916642166093
585848058327971863158257619930226042698661632905146850162960633520155118628867911625
239725418415604877699453370534194837316774432534349898272185517986005836675979188507
704257742239368667474408667895362250511057160490511029003928521905584001998500412272
300652930331121107733643816582958394189572596322595033481338694429893546070448926193
272806103607662243076062238492673013489615386273692928543218155895489937520257687664
947027647847750945509362588170852889875925160078794611182855714905968753089053225774
863189760920183769031795458368827168630624310066175033265292467587132663811805301906
7641362643313498166787213628751583911774745199740840719668395714479929
Notice, of course, that the units digit is 9.
|
93 videos|78 docs|104 tests
|
FAQs on Difficult Units Digits Questions - Quantitative Reasoning for GRE
| 1. What is the concept of units digit arithmetic? |  |
| 2. How can units digit arithmetic be helpful in solving problems on the GMAT? |  |
| 3. Are there any specific rules or patterns to determine the units digit of a number raised to a power? |  |
| 4. Can units digit arithmetic be applied to fractions and decimals as well? |  |
| 5. Are there any common mistakes to avoid when using units digit arithmetic? |  |





















