Vector Spaces & Matrices | Basic Physics for IIT JAM PDF Download
Vector Spaces:
Let  be field and let
be field and let  be a set.
be a set.  is said to be a Vector Space over
is said to be a Vector Space over  along with the binary operations of addition and scalar product if
along with the binary operations of addition and scalar product if
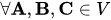
(i)  ...(Commutativity)
...(Commutativity)
(ii) 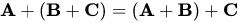 ...(Associativity)
...(Associativity)
(iii)  such that
such that 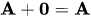 ...(Identity)
...(Identity)
(iv)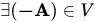 such that
such that 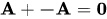 ...(Inverse)
...(Inverse)
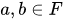
(v) 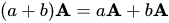
(vi)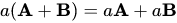
(vii)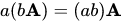
The elements of  are called vectors while the elements of
are called vectors while the elements of  are called scalars. In most problems of Physics, the field
are called scalars. In most problems of Physics, the field  of scalars is either the set of real numbers
of scalars is either the set of real numbers  or the set of complex numbers
or the set of complex numbers  .
.
Examples of vector spaces:
(i) The set  over
over  can be visualised as the space of ordinary vectors "arrows" of elementary Physics.
can be visualised as the space of ordinary vectors "arrows" of elementary Physics.
(ii) The set of all real polynomials 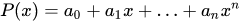 is a vector space over
is a vector space over 
(iii) Indeed, the set of all functions 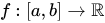 is also a vector spaces over
is also a vector spaces over  , with addition and scalar multiplication defined as is usual.
, with addition and scalar multiplication defined as is usual.
Although the idea of vectors as "arrows" works well in most examples of vector spaces and is useful in solving problems, the latter two examples were deliberately provided as cases where this intuition fails to work.
Basis:
A set E ⊂ V is said to be linearly independent if and only if
a1E1 + a2E2 + ... + anEn =0 implies that a1 =a2 = ... =0, whenever E1, E2,....En ∈ E
A set E ⊂ V is said to cover V if for every A ∈ V there exist e1,e2,... such that A = e1E1 + e2E2 + ... (we leave the question of finiteness of the number of terms open at this point)
A set E ⊂ V is said to be a basis for V if B is linearly independent and if B covers V.
If a vector space has a finite basis with n elements, the vetor space is said to be n-dimensional
As an example, we can consider the vector space R3 over reals. The vectors (1,0,0); (0,1,0); (0,0,1) form one of the several possible basis for R3. These vectors are often denoted as 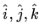 or as
or as 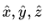
Theorem:
Let V be a vector space and let B={b1,b2,...,bn} be a basis for V. Then any subset of V with n+1 elements is linearly dependent.
Proof :
Let E ⊂ V with E = {u1,u2,..,un+1}
By definition of basis, there exist scalars a1i,a2i,...,ani such that ui = 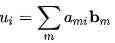
Hence we can write 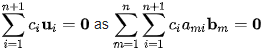 that is
that is
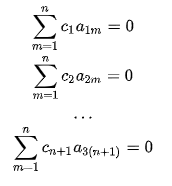
Which has a nontrivial solution for ci. Hence E is linearly dependent.
If a vector space has a finite basis of n elements, we say that the vector space is n-dimensional
Inner Product:
An in-depth treatment of inner-product spaces will be provided in the chapter on Hilbert Spaces. Here we wish to provide an introduction to the inner product using a basis.
Let V be a vector space over R and let B={b1,b2,...,bn} be a basis for V. Thus for every member u of V, we can write 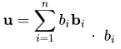 are called the components of u with respect to the basis B.
are called the components of u with respect to the basis B.
We define the inner product as a binary operation (.) : V x V → R as 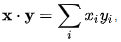 , where xi,yi are the components of x,y with respect to B
, where xi,yi are the components of x,y with respect to B
Note here that the inner product so defined is intrinsically dependent on the basis. Unless otherwise mentioned, we will assume the basis 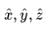 while dealing with inner product of ordinary "vectors".
while dealing with inner product of ordinary "vectors".
Linear Transformations:
Let U, V be vector spaces over F. A function T : U → V is said to be a Linear transformation if for all u1, u2 ∈ U and c ∈ F if
(i)T(u1 + u2) = T(u1) + T(u2)
(ii)T(cu1) = cT(u1)
Now let E = {e1,e2,...,em} and F = {f1,f2,...,fn} be bases for U,V respectively.
Let e′i =T(e1). As F is a basis, we can write 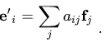
Thus, by linearity we can say that if T(u) =v, we can write the components uj of v in terms of those of u as 
The collection of coefficients aij is called a matrix, written as
 and we can say that T can be represented as a matrix A with respect to the bases E,F
and we can say that T can be represented as a matrix A with respect to the bases E,F
Eigenvalue Problems:
Let V be a vector space over reals and let T : V → V be a linear transformations.
Equations of the type Tu = λu, to be solved for u ∈ V and λ ∈ R are called eigenvalue problems. The solutions λ are called eigenvalues of T while the corresponding u are called eigenvectors or eigenfunctions. (Here we take Tu = T(u) )
Matrices
Definition:
Let F be a field and let M = {1,2,...,m}, N = {1,2,...n}. An n×m matrix is a function A :N x M → F.
We denote A(ij) = aij. Thus, the matrix A can be written as the array of numbers A = 
Consider the set of all n×m matrices defined on a field F. Let us define scalar product cA to be the matrix B whose elements are given by bij = caij. Also let addition of two matrices A + B be the matrix C whose elements are given by cij = aij + bij
With these definitions, we can see that the set of all n×m matrices on F form a vector space over F
Linear Transformations:
Let U, V be vector spaces over the field F Consider the set of all linear transformations T : U → V .
Define addition of transformations as (T1+ T2 ) 1 1 = T1u - T2u and scalar product as (CT)u =c(Tu). Thus, the set of all linear transformations from U to V is a vector space. This space is denoted as L(U, V).
Observe that L(U, V) is an run dimensional vector space
Operations on Matrices:
Determinant:
The determinant of a matrix is defined iteratively (a determinant can be defined only if the matrix is square). If A is a matrix, its determinant is denoted as 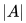
We define , 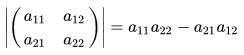
For n=3, we define 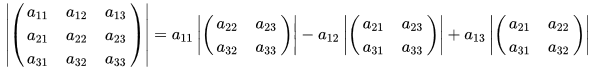
we thus define the determinant for any square matrix
Trace:
Let A be an n×n (square) matrix with elements aij
The trace of A is defined as the sum of its diagonal elements, that is,
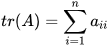
This is conventionally denoted as 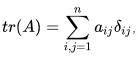 where
where 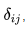 called the Kronecker delta is a symbol which you will encounter constantly in this book. It is defined as
called the Kronecker delta is a symbol which you will encounter constantly in this book. It is defined as
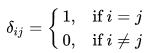
The Kronecker delta itself denotes the members of an n×n matrix called the n×n unit matrix, denoted as I
Transpose:
Let A be an m×n matrix, with elements aij. The n×m matrix AT with elements 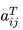 is called the transpose of A when
is called the transpose of A when 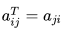
Matrix Product:
Let A be an m×n matrix and let B be an n×p matrix.
We define the product of A,B to be the m×p matrix C whose elements are given by
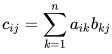 and we write C =AB
and we write C =AB
Properties:
(i) Product of matrices is not commutative. Indeed, for two matrices A,B, the product BA need not be well-defined even though AB can be defined as above.
(ii) For any matrix n×n A we have AI = IA = A, where I is the n×n unit matrix.
|
217 videos|156 docs|94 tests
|
FAQs on Vector Spaces & Matrices - Basic Physics for IIT JAM
| 1. What is a vector space? |  |
| 2. How are matrices related to vector spaces? |  |
| 3. What are the properties of a vector space? |  |
| 4. How do vector spaces and matrices relate to physics? |  |
| 5. Can vector spaces and matrices be applied to quantum mechanics? |  |
















