Divergence, Curl and Gradient | Basic Physics for IIT JAM PDF Download
Vector and Scalar Fields
Definition
Let C : R3 →F , where F is a field. We say that C is a scalar field
In the physical world, examples of scalar fields are
(i) The electrostatic potential 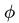 in space
in space
(ii) The distribution of temperature in a solid body, T(r)
Definition
Let V be a vector space. Let F : R3 → V, we say that F is a vector field; it associates a vector from V with every point of R3.
In the physical world, examples of vector fields are
(i) The electric and magnetic fields in space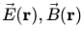
(ii) The velocity field in a fluid 
The Gradient
Let C be a scalar field. We define the gradient as an "operator" ∇ mapping the field C to a vector in R3 such that
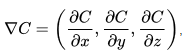 or as is commonly denoted
or as is commonly denoted 
We shall encounter the physicist's notion of "operator" before defining it formally in the chapter Hilbert Spaces. It can be loosely thought of as "a function of functions"
Gradient and the total derivative
Recall from multivariable calculus that the total derivative of a function f : R3 →R at a ∈ R3 is defined as the linear transformation A that satisfies
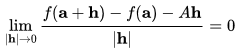
In the usual basis, we can express as the row matrix 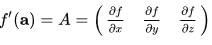
It is customary to denote vectors as column matrices. Thus we may write 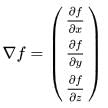
The transpose of a matrix given by constituents aij is the matrix with constituents 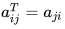
Thus, the gradient is the transpose of the total derivative.
Divergence
Let F : R3 → R3 be a vector field and let F be differentiable.
We define the divergence as the operator (∇.) mapping F to a scalar such that
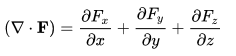
Curl
Let F : R3 → R3 be a vector field and let F be differentiable.
We define the curl as the operator ( ∇ x) mapping F to a linear transformation from R3 onto itself such that the linear transformation can be expressed as the matrix
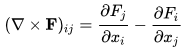 written in short as
written in short as 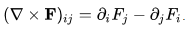 Here, x1,x2,x3 denote x,y,z and so on.
Here, x1,x2,x3 denote x,y,z and so on.
the curl can be explicitly given by the matrix: 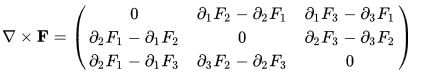
this notation is also sometimes used to denote the vector exterior or cross product, 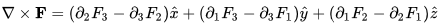
|
217 videos|156 docs|94 tests
|
FAQs on Divergence, Curl and Gradient - Basic Physics for IIT JAM
| 1. What is divergence in physics? |  |
| 2. What does the curl of a vector field represent? |  |
| 3. How is gradient used in physics? |  |
| 4. What is the relationship between divergence and curl? |  |
| 5. How are divergence, curl, and gradient related to each other? |  |
















