Alternating Electric Current: Resonance | Basic Physics for IIT JAM PDF Download
A most interesting condition known as resonance occurs when the phase angle is zero in equation (31), or equivalently, when the angular frequency ω has the value ω = ωr = Square root of√1/LC. The impedance in equation (30) then has its minimum value and equals the resistance R. The amplitude of the current in the circuit, i0, is at its maximum value (see equation [29]). Figure 24 shows the dependence of i0 on the angular frequency ω of the source of alternating electromotive force. The values of the electric parameters for the figure are V0 = 50 volts, R = 25 ohms, L = 4.5 millihenrys, and C = 0.2 microfarad. With these values, the resonant angular frequency ωr of the circuit in Figure 23 is 3.33 × 104 radians per second.
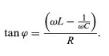
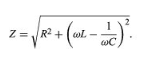
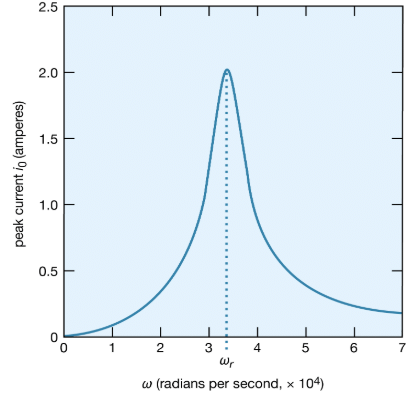
The peaking in the current shown in Figure 24 constitutes a resonance. At the resonant frequency, in this case when ωr equals 3.33 × 104 radians per second, the impedance Z of the circuit is at a minimum and the power dissipated is at a maximum. The phase angle ϕ is zero so that the current is in phase with the driving voltage, and the power factor, cos ϕ, is 1. Figure 25 illustrates the variation of the average power with the angular frequency of the sinusoidal electromotive force. The resonance is seen to be even more pronounced. The quality factor Q for the circuit is the electric energy stored in the circuit divided by the energy dissipated in one period. The Q of a circuit is an important quantity in certain applications, as in the case of electromagnetic waveguides and radio-frequency cavities where Q has values around 10,000 and where high voltages and electric fields are desired. For the present circuit, Q = ωrL/R. Qalso can be obtained from the average power graph as the ratio ωr/(ω2 − ω1), where ω1 and ω2are the angular frequencies at which the average power dissipated in the circuit is one-half its maximum value. For the circuit here, Q = 6.
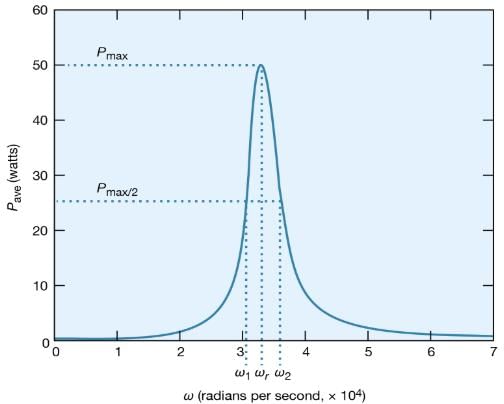
Figure: Average power dissipation versus ω (see text).
What is the maximum value of the potential difference across the inductor? Since it is given by Ldi/dt, it will occur when the current has the maximum rate of change.Figure 26 shows the amplitude of the potential difference as a function of ω.
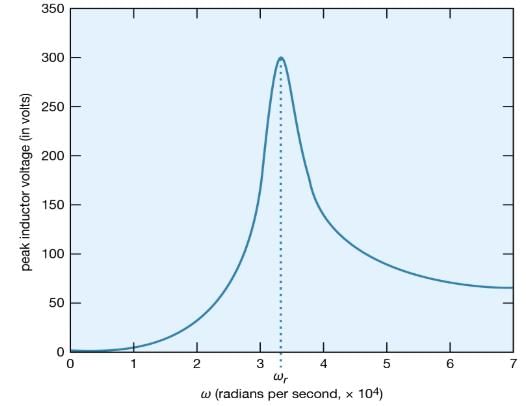
The maximum amplitude of the voltage across the inductor, 300 volts, is much greater than the 50-volt amplitude of the driving sinusoidal electromotive force. This result is typical of resonance phenomena. In a familiar mechanical system, children on swings time their kicks to attain very large swings (much larger than they could attain with a single kick). In a more spectacular, albeit costly, example, the collapse of the Tacoma Narrows Bridge (a suspension bridge across the Narrows of Puget Sound, Washington) on November 7, 1940, was the result of the large amplitudes of oscillations that the span attained as it was driven in resonance by high winds. A ubiquitous example of electric resonance occurs when a radio dial is turned to receive a broadcast. Turning the dial changes the value of the tuning capacitor of the radio. When the circuit attains a resonance frequency corresponding to the frequency of the radio wave, the voltage induced is enhanced and processed to produce sound.
|
217 videos|156 docs|94 tests
|
















