Mathematics Exam > Mathematics Notes > Algebra > Representation of Functions
Representation of Functions | Algebra - Mathematics PDF Download
Representation of Functions
The function is the connection or the link between two sets and can be represented in different ways. Consider the above example of the printing machine. The function that shows the relationship between the numbers of seconds (x) and the numbers of lines printed (y). We are quite familiar with functions and now we will learn how to represent them.
Algebraic Representation
Here, we will represent the function by a simple algebraic equation which is: f(x) = y = 100 + 15(x). For different values of x, the values of y (= f(x)) change accordingly. What if, one wants to know about the numbers of lines printed by the machine in 15 seconds? Simple, Numbers of words printed = y = 100 + 15 (15) = 325.
Table Representation
In this method, we represent the relationship in the form of a table. For each value of x (input), there is one and only one value of y (output). The table representation of the problem:
Graphical Representation
Here, we will draw a graph showing the connection between the two elements of two sets say x and y such that x ∈ X and y ∈ Y. Plotting the satisfying points of x and y in the respective axes. Drawing a straight line passing through these points will represent the function in a graphical way. Graphical representation of the above problem:
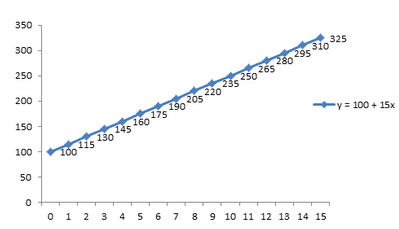
Solved Examples for You
Problem: Consider an auto-driver who charges Rs. 15 for the first 7 km and subsequently charges an additional fare of Rs. 5 for each km. Find the cost one has to pay for 12 km by representing in tabular form.
Solution: Let x be the difference in distance (km) the auto ran and y be the fare of the auto for different distances (in Rs.). The equation of the given problem is: f(x) = y = 15 + 5 (x). The difference in distance travelled by auto is 12 – 7 = 5 km and we are required to find the fare for it. In tabular form, the above problem is
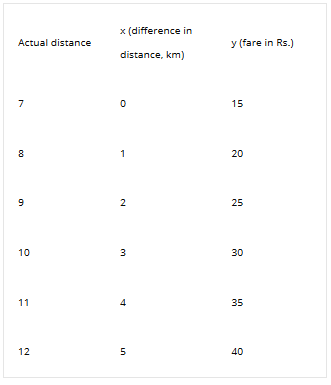
One has to pay Rs. 40 for travelling a distance of 12 km.
The document Representation of Functions | Algebra - Mathematics is a part of the Mathematics Course Algebra.
All you need of Mathematics at this link: Mathematics
|
161 videos|58 docs
|
FAQs on Representation of Functions - Algebra - Mathematics
| 1. What is the definition of a function in mathematics? |  |
Ans. In mathematics, a function is a relation between a set of inputs, called the domain, and a set of outputs, called the range, such that each input is related to exactly one output. It can be represented by an equation, a graph, or a table.
| 2. How can functions be represented graphically? | |
Ans. Functions can be represented graphically by plotting points on a coordinate plane. Each point corresponds to an input-output pair of the function. By connecting these points, a smooth curve or line can be formed, which represents the function graphically.
| 3. What is the difference between a one-to-one function and an onto function? | |
Ans. A one-to-one function is a function in which each input is related to a unique output. In other words, no two different inputs can have the same output. On the other hand, an onto function, also known as a surjective function, is a function in which every element in the range is mapped to by at least one element in the domain.
| 4. How can the domain and range of a function be determined? | |
Ans. The domain of a function is the set of all possible inputs or x-values for which the function is defined. It can be determined by looking for any restrictions or limitations on the independent variable. The range of a function is the set of all possible outputs or y-values that the function can produce. It can be determined by examining the values that the dependent variable can take.
| 5. What are some real-life examples of functions? | |
Ans. Functions are used to model various real-life situations. Some examples include the distance traveled by a car over time, the temperature of a room as a function of time, the height of a ball thrown in the air as a function of time, the sales of a product as a function of price, and the population growth of a city as a function of time.
Related Exams
About this Document
|
4.81/5 Rating |
|
Dec 23, 2024 Last updated |
Document Description: Representation of Functions for Mathematics 2024 is part of Algebra preparation.
The notes and questions for Representation of Functions have been prepared according to the Mathematics exam syllabus. Information about Representation of Functions covers topics
like and Representation of Functions Example, for Mathematics 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Representation of Functions.
Introduction of Representation of Functions in English is available as part of our Algebra
for Mathematics & Representation of Functions in Hindi for Algebra course.
Download more important topics related with notes, lectures and mock test series for Mathematics
Exam by signing up for free. Mathematics: Representation of Functions | Algebra - Mathematics
Description
Full syllabus notes, lecture & questions for Representation of Functions | Algebra - Mathematics - Mathematics | Plus excerises question with solution to help you revise complete syllabus for Algebra | Best notes, free PDF download
Information about Representation of Functions
In this doc you can find the meaning of Representation of Functions defined & explained in the simplest way possible. Besides explaining types of
Representation of Functions theory, EduRev gives you an ample number of questions to practice Representation of Functions tests, examples and also practice Mathematics
tests
|
Explore Courses for Mathematics exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Objective type Questions
,Exam
,practice quizzes
,Previous Year Questions with Solutions
,Extra Questions
,MCQs
,Free
,mock tests for examination
,shortcuts and tricks
,Sample Paper
,Representation of Functions | Algebra - Mathematics
,Viva Questions
,Summary
,Semester Notes
,study material
,Representation of Functions | Algebra - Mathematics
,ppt
,Representation of Functions | Algebra - Mathematics
,video lectures
,Important questions
,past year papers
,
Additional Information about Representation of Functions for Mathematics Preparation
Representation of Functions Free PDF Download
The Representation of Functions is an invaluable resource that delves deep into the core of the Mathematics exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Representation of Functions now and kickstart your journey towards success in the Mathematics exam.
Importance of Representation of Functions
The importance of Representation of Functions cannot be overstated, especially for Mathematics aspirants.
This document holds the key to success in the Mathematics exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Representation of Functions Notes
Representation of Functions Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Representation of Functions.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Representation of Functions Notes on EduRev are your ultimate resource for success.
Representation of Functions Mathematics Questions
The "Representation of Functions Mathematics Questions" guide is a valuable resource for all aspiring students preparing for the
Mathematics exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Representation of Functions on the App
Students of Mathematics can study Representation of Functions alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Representation of Functions,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Representation of Functions is prepared as per the latest Mathematics syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup