Types of Functions | Algebra - Mathematics PDF Download
What does the word function stand for? By the word function, we understand the responsibility or role one has to play. What is the function of the leaves of plants – to prepare food for the plant and store them? What is the function of the roots of plants? They absorb water and other nutrients from the ground and supply it to the plants and help them stand erect. Can we say that everyone has different types of functions? Let’s learn about some types of function in mathematics!
Functions
We can define a function as a special relation which maps each element of set A with one and only one element of set B. Both the sets A and B must be non-empty. A function defines a particular output for a particular input. Hence, f: A → B is a function such that for a ∈ A there is a unique element b ∈ B such that (a, b) ∈ f
Types of Functions
We have already learned about some types of functions like Identity, Polynomial, Rational, Modulus, Signum, Greatest Integer functions. In this section, we will learn about other types of function.
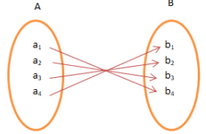
One to One Function
A function f: A → B is One to One if for each element of A there is a distinct element of B. It is also known as Injective. Consider if a1 ∈ A and a2 ∈ B, f is defined as f: A → B such that f (a1) = f (a2)
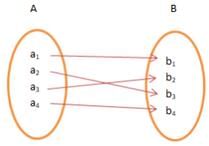
Many to One Function
It is a function which maps two or more elements of A to the same element of set B. Two or more elements of A have the same image in B.
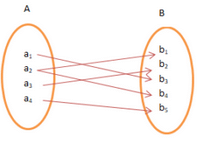
Onto Function
If there exists a function for which every element of set B there is (are) pre-image(s) in set A, it is Onto Function. Onto is also referred as Surjective Function.
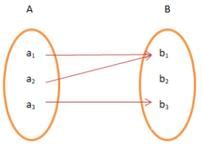
One – One and Onto Function
A function, f is One – One and Onto or Bijective if the function f is both One to One and Onto function. In other words, the function f associates each element of A with a distinct element of B and every element of B has a pre-image in A.
Other Types of Functions
A function is uniquely represented by its graph which is nothing but a set of all pairs of x and f(x) as coordinates. Let us get ready to know more about the types of functions and their graphs.
Identity Function
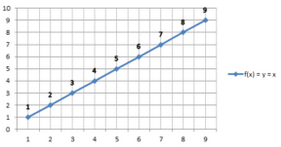
Let R be the set of real numbers. If the function f: R→R is defined as f(x) = y = x, for x ∈ R, then the function is known as Identity function. The domain and the range being R. The graph is always a straight line and passes through the origin.
Constant Function
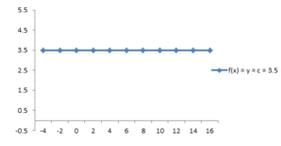
If the function f: R→R is defined as f(x) = y = c, for x ∈ R and c is a constant in R, then such function is known as Constant function. The domain of the function f is R and its range is a constant, c. Plotting a graph, we find a straight line parallel to the x-axis.
Polynomial Function
A polynomial function is defined by y =a0 + a1x + a2x2 + … + anxn, where n is a non-negative integer and a0, a1, a2,…, n ∈ R. The highest power in the expression is the degree of the polynomial function. Polynomial functions are further classified based on their degrees:
- Constant Function: If the degree is zero, the polynomial function is a constant function (explained above).
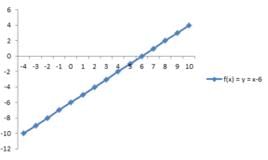
- Linear Function: The polynomial function with degree one. Such as y = x + 1 or y = x or y = 2x – 5 etc. Taking into consideration, y = x – 6. The domain and the range are R. The graph is always a straight line.
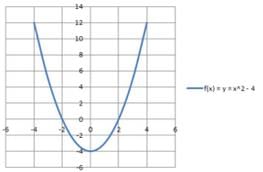
Quadratic Function: If the degree of the polynomial function is two, then it is a quadratic function. It is expressed as f(x) = ax2 + bx + c, where a ≠ 0 and a, b, c are constant & x is a variable. The domain and the range are R. The graphical representation of a quadratic function say, f(x) = x2 – 4 is
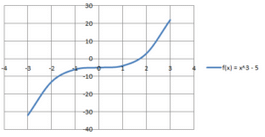
- Cubic Function: A cubic polynomial function is a polynomial of degree three and can be denoted by f(x) = ax3 + bx2 + cx +d, where a ≠ 0 and a, b, c, and d are constant & x is a variable. Graph for f(x) = y = x3 – 5. The domain and the range are R.
Rational Function
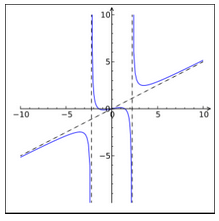
A rational function is any function which can be represented by a rational fraction say, f(x)/g(x) in which numerator, f(x) and denominator, g(x) are polynomial functions of x, where g(x) ≠ 0. Let a function f: R → R is defined say, f(x) = 1/(x + 2.5). The domain and the range are R. The Graphical representation shows asymptotes, the curves which seem to touch the axes-lines.
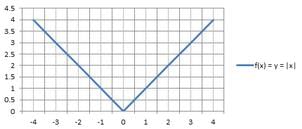
Modulus Function
The absolute value of any number, c is represented in the form of |c|. If any function f: R→ R is defined by f(x) = |x|, it is known as Modulus Function. For each non-negative value of x, f(x) = x and for each negative value of x, f(x) = -x, i.e.,
f(x) = {x, if x ≥ 0; – x, if x < 0.
Its graph is given as, where the domain and the range are R.
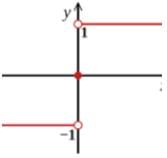
Signum Function
A function f: R→ R defined by
f(x) = { 1, if x > 0; 0, if x = 0; -1, if x < 0
Signum or the sign function extracts the sign of the real number and is also known as step function.
Greatest Integer Function
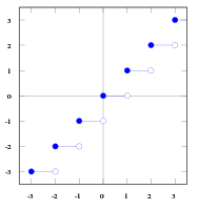
If a function f: R→ R is defined by f(x) = [x], x ∈ X. It round-off to the real number to the integer less than the number. Suppose, the given interval is in the form of (k, k+1), the value of greatest integer function is k which is an integer. For example: [-21] = 21, [5.12] = 5. The graphical representation is
Solved Example for You
Question: Which of the following is a function?
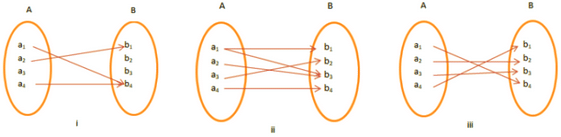
Solution: Figure (iii) is an example of a function. Since the given function maps every element of A with that of B. In figure (ii), the given function maps one element of A with two elements of B (one to many). Figure (i) is a violation of the definition of the function. The given function does not map every element of A.
|
161 videos|58 docs
|
FAQs on Types of Functions - Algebra - Mathematics
| 1. What are the different types of functions in mathematics? |  |
| 2. What is a linear function and how is it represented? |  |
| 3. How do we define a quadratic function and what is its graph like? |  |
| 4. What are exponential functions and what makes them unique? |  |
| 5. Can you explain the concept of trigonometric functions and their applications? |  |




















