Problems for Practice - Complex Numbers | Algebra - Mathematics PDF Download
Complex Numbers - Practice Problems
Perform the indicated operation and write your answer in standard form.
Q.1. (4−5i)(12+11i)(4−5i)(12+11i)
Ans. We know how to multiply two polynomials and so we also know how to multiply two complex numbers. All we need to do is “foil” the two complex numbers to get,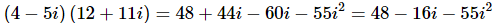
All we need to do to finish the problem is to recall that i2=−1. Upon using this fact we can finish the problem.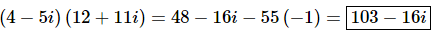
Q.2. (−3−i)−(6−7i)
Ans. We know how to subtract two polynomials and so we also know how to subtract two complex numbers.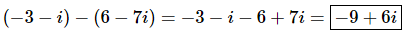
Q.3. (1+4i)−(−16+9i)
Ans. We know how to subtract two polynomials and so we also know how to subtract two complex numbers.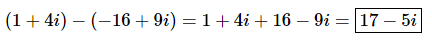
Q.4. 8i(10+2i)
Ans. We know how to multiply two polynomials and so we also know how to multiply two complex numbers. All we need to do is distribute the 8i to get,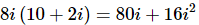
All we need to do to finish the problem is to recall that i2=−1. Upon using this fact we can finish the problem.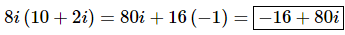
Q.5. (−3−9i)(1+10i)
Ans. We know how to multiply two polynomials and so we also know how to multiply two complex numbers. All we need to do is “foil” the two complex numbers to get,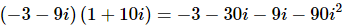
All we need to do to finish the problem is to recall that i2=−1. Upon using this fact we can finish the problem.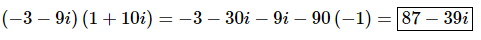
Q.6. (2+7i)(8+3i)
Ans. We know how to multiply two polynomials and so we also know how to multiply two complex numbers. All we need to do is “foil” the two complex numbers to get,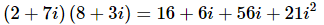
All we need to do to finish the problem is to recall that i2=−1. Upon using this fact we can finish the problem.
Q.7. 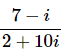
Ans. Because standard form does not allow for i’s to be in the denominator we’ll need to multiply the numerator and denominator by the conjugate of the denominator, which is 2−10i.
Multiplying by the conjugate gives,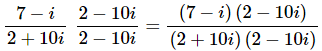
Now all we need to do is do the multiplication in the numerator and denominator and put the result in standard form.
Q.8. 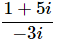
Ans. Because standard form does not allow for ii’s to be in the denominator we’ll need to multiply the numerator and denominator by the conjugate of the denominator, which is 3i.
Multiplying by the conjugate gives,
Now all we need to do is do the multiplication in the numerator and denominator and put the result in standard form.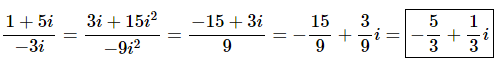
Q.9.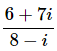
Ans. Because standard form does not allow for i’s to be in the denominator we’ll need to multiply the numerator and denominator by the conjugate of the denominator, which is 8+i.
Multiplying by the conjugate gives,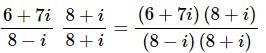
Now all we need to do is do the multiplication in the numerator and denominator and put the result in standard form.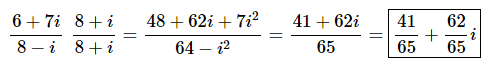
|
181 videos|58 docs
|
FAQs on Problems for Practice - Complex Numbers - Algebra - Mathematics
| 1. What are complex numbers and how are they used in mathematics? |  |
| 2. How are complex numbers represented and written? |  |
| 3. What is the geometric interpretation of complex numbers? |  |
| 4. How are complex numbers added and subtracted? |  |
| 5. What is the complex conjugate and why is it important? |  |





















