Area of a Triangle Using Determinants | Algebra - Mathematics PDF Download
Determinants
A determinant of a square matrix [aij] of order n where aij = (i, j)th element of A is a number (real or complex) associated with it. The number of rows is the same as the number of the columns in a square matrix. If A is a square matrix such as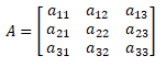
Then determinant of A is |A| = Δ = a11 [(a22 × a33) – (a23 × a32)] – a12 [(a21 × a33) – (a31 × a23)] + a13 [(a21 × a32) – (a31 × a22)].
Determinants and Matrices as Equation Solver
Since now we are familiar with the way of calculating the determinant of a square matrix. Here, we will discuss the way to solve a system of linear equations in two or three variables. With the help of the determinant, we can also check for the consistency of linear equations.
• Consistent System: If one or more solution(s) exists for a system of equations then it is a consistent system
• Inconsistent System: A system of equations with no solution is an inconsistent system.
The Solution of System of Linear Equations
A solution for a system of linear Equations can be found by using the inverse of a matrix. Suppose we have the following system of equations
a11 x + a12 y + a13 z = b1
a21 x + a22 y + a23 z = b2
a31 x + a32 y + a33 z = b3
where, x, y, and z are the variables and a11, a12, … , a33 are the respective coefficients of the variables and b1, b2, and b3 are the constants. We need to find the solution for the values of the variables in this system of equations.
Determinant as an Equation Solver
The above system of equations can be represented in the form of a square matrix as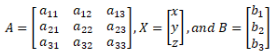
i.e., AX = B or,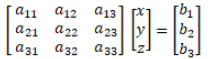
Here arise two cases
Case1
If A is a non-singular matrix i.e., |A| ≠ 0, then its inverse exists.
We have A X = B
or, A–1 (A X) = A–1 B (pre-multiplying by A–1)
or, (A–1 A) X = A–1 B
and, IX = A– 1 B (I is the identity matrix)
or, X = A–1 B where, A–1 = (adj A)/|A|
This matrix equation provides a unique solution and is known as the Matrix Method.
Case2
If A is a singular matrix, then |A| = 0 then we calculate (adj A) B. If (adj A) B ≠ 0 (zero matrix), then the solution does not exist. The system of equations is inconsistent. Else, if (adj A) B = 0 then the system will either have infinitely many solutions (consistent system) or no solution (inconsistent system).
Solved Example for You
Problem: Suppose you have three numbers. The sum of the two numbers and the twice of the second equals 2. The sum of the second and third when subtracted from the twice of first gives 1. The difference of thrice of first and five times the third gives 5. Rewrite the statement in form of the system of equations. Solve it using Matrix Method as an equation solver.
Solution: Assume that x, y, and z are the three numbers. Rewriting the above statement we have the following system of equations
x + 2y + z = 2
2x – y – z = 1
3x – 5y = 5
In matrix notation, we have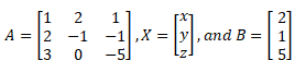
Here, the determinant of A = |A| = 1(5 – 0) – 2(–10 + 3) + 1(0 + 3) = 22 ≠ 0. Hence there exists a unique solution for X.
Calculating adj (A), we have Aij = (–1)(i + j) Mij , where Mij is the co-factor of aij
• A11 = 1(5 – 0) = 5, A12 = –1(–10 + 3) = 7, A13 = 1(0 + 3) = 3,
• A21 = –1(–10 –0) = 10, A22 = 1(–5 – 3) = –8, A23 = –1(0 – 6) = 6,
• A31 = 1(–2 + 1) = –1, A32 = –1(–1 – 2) = 3, A33 = 1(–1 – 4) = –5
The inverse of the matrix A is A−1.
Since X = A– 1 B
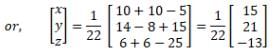
Thus, x = 15/22, y = 21/22, and z = –13/22.
Definition of Adjoint of a Matrix
The adjoint of a square matrix A = [aij]n x n is defined as the transpose of the matrix [Aij]n x n, where Aij is the cofactor of the element aij. Adjoing of the matrix A is denoted by adj A.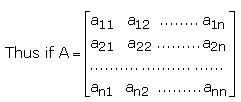
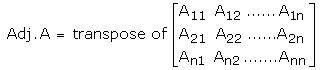
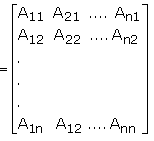
Example 1: Find the adjoint of the matrix: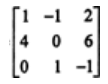
Solution: We will first evaluate the cofactor of every element,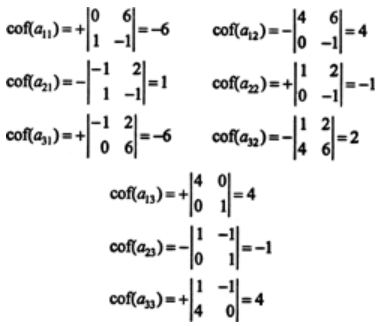
Therefore,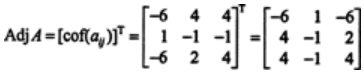
The Relation between Adjoint and Inverse of a Matrix
To find the inverse of a matrix A, i.e A-1 we shall first define the adjoint of a matrix. Let A be an n x n matrix. The (i,j) cofactor of A is defined to be
Aij = (-1)ij det(Mij),
where Mij is the (i,j)th minor matrix obtained from A after removing the ith row and jth column. Let’s consider the n x n matrix A = (Aij) and define the n x n matrix Adj(A) = AT. The matrix Adj(A) is called the adjoint of matrix A. When A is invertible, then its inverse can be obtained by the formula given below.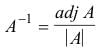
The inverse is defined only for non-singular square matrices. The following relationship holds between a matrix and its inverse:
AA-1 = A-1A = I, where I is the identity matrix.
Example 2: Determine whether the matrix given below is invertible and if so, then find the invertible matrix using the above formula.
Solution: Since A is an upper triangular matrix, the determinant of A is the product of its diagonal entries. This, we have det(A) = -1, which is a non-zero value and hence, A is invertible. To find the inverse using the formula, we will first determine the cofactors Aij of A. We have,
Then the adjoint matrix of A is
Using the formula, we will obtain the inverse matrix as
Theorems on Adjoint and Inverse of a Matrix
Theorem 1
If A be any given square matrix of order n, then A adj(A) = adj(A) A = |A|I, where I is the identitiy matrix of order n.
Proof: Let
Since the sum of the product of elements of a row (or a column) with corresponding cofactors is equal to |A| and otherwise zero, we have
Similarly, we can show that adj(A) A = |A| I
Hence, A adj(A) = adj(A) A
Theorem 2
If A and B are non-singular matrices of the same order, then AB and BA are also non-singular matrices of the same order.
Theorem 3
The determinant of the product matrices is equal to the product of their respective determinants, that is, |AB| = |A||B|, where A and B are square matrices of the same order.
Remark: We know that
Writing determinants of matrices on both sides, we have
i.e,
i.e, |adj(A)| |A| = |A|3
or |adj(A)| = |A|2
In general, if A is a quare matrix of order n, then |adj(A)| = |A|n-1.
Theorem 4
A square matrix A is invertible if and only if A is a non-singular matrix.
Proof: Let A be an invertible matrix of order n and I be the identity matrix of the same order. Then there exists a square matrix B of order n such that AB = BA = I. Now, AB = I.
So |A| |B| = |I| = 1 (since |I| = 1 and |AB| = |A| |B|). This gives |A| to be a non-zero value. Hence A is a non-singular matrix. Conversely, let A be a non-singular matrix, then |A| is non-zero. Now A adj(A) = adj(A) A = |A| I (Theorem 1). Or,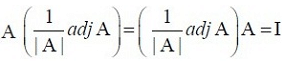
or AB = BA = I, where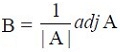
Thus A is invertible and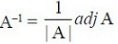
Solved Examples for You
Question: With 1, ω, ω2 as cube roots of units, inverse of which of the following matrices exist?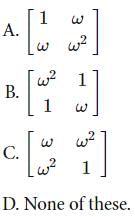
Solution: Option D. Inverse of a matrix exists if its determinant if not equal to 0. For option A, B and C, the determinants are equal to zero, hence the inverse does not exist for any of the given matrices.
|
181 videos|58 docs
|
FAQs on Area of a Triangle Using Determinants - Algebra - Mathematics
| 1. What is the formula for finding the area of a triangle using determinants? |  |
| 2. How do determinants help in finding the area of a triangle? |  |
| 3. Are there any other methods to find the area of a triangle apart from using determinants? |  |
| 4. Can determinants be used to find the area of any type of triangle? |  |
| 5. Can determinants be used to find the area of a triangle in three-dimensional space? |  |
















