Question For Practice With Solutions:- Normed Linear Spaces | Additional Topics for IIT JAM Mathematics PDF Download
Problems based on Module –I (Metric Spaces)
Ex.1. Let d be a metric on X. Determine all constants K such that
(i) kd , (ii) d + k is a metric on X
Hint.1: Use definition . Ans (i) k>0 (ii) k=0
Ex.2. Show that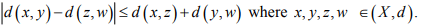
Hint.2: Use Triangle inequality d 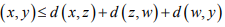
Similarity, 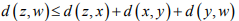
Ex.3. Find a sequence x which is in lp with p >1 but 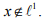
Hint.3: Choose x = (xk) where xk = 1/k
Ex.4. Let (X,d) be a metric space and A,B are any two non empty subsets of X. Is D(A,B) = inf d (a,b)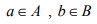 a metric on the power set of X?
a metric on the power set of X?
Hint.4: No. Because D(A,B)=0 ≠ > A=B e.g. Choose 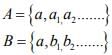 where ai ≠ bi clearly
where ai ≠ bi clearly 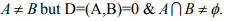
Ex.5. Let ( X, d) be any metric space. Is 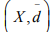 a Metric space where
a Metric space where 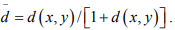
Hint.5: Yes. ;
Ex.6. Let (X1, d1) and (X2, d2) be metric Spaces and X = X1 X2. Are 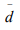 as defined below A metric on X?
as defined below A metric on X?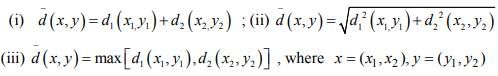
Hint.6: Yes.
Ex.7. Show that in a discrete metric space X, every subset is open and closed.
Hint.7: Any subset is open since for any a ∈ A, the open ball 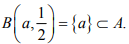 Similarly Ac is open, so that (Ac)c = A is closed.
Similarly Ac is open, so that (Ac)c = A is closed.
Ex.8. Describe the closure of each of the following Subsets:
(a) The integers on R.
(b) The rational numbers on R.
(c) The complex number with real and imaginary parts as rational in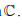 .
.
(d) The disk 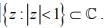
Hint.8: use Definition
Ans (a) The integer, (b) R, (c) 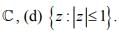
Ex.9. Show that a metric space X is separable if and only if X has a countable subset Y with the property: For every ∈ > 0 and every x ∈ X there is a y ∈ Y such that d (x ,y) < ∈.
Hint.9: Let X be separable .So it has a countable dense subset Y i.e. 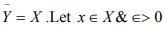 be given.Since Y is dense in X and
be given.Since Y is dense in X and 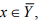 so that the ∈ neibourhood B(x;∈) of x contains a y ∈ Y, and d (x, y) < ∈. Conversely, if X has a countable subset Y with the property given in the problem, every x ∈ X is a point of Y or an accumulation point of Y. Hence x ∈ Y, s result follows.
so that the ∈ neibourhood B(x;∈) of x contains a y ∈ Y, and d (x, y) < ∈. Conversely, if X has a countable subset Y with the property given in the problem, every x ∈ X is a point of Y or an accumulation point of Y. Hence x ∈ Y, s result follows.
Ex.10. If (xn) and (yn) are Cauchy sequences in a metric space (X,d), show that (an), where an = d(xn.yn) converges.
Hint.10: Since 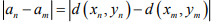
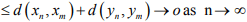 which shows that (an) is a Cauchy sequence of real numbers . Hence convergent.
which shows that (an) is a Cauchy sequence of real numbers . Hence convergent.
Ex.11. Let ab ∈ R and a < b.Show that the open interval (a, b) is an incomplete subspace of R.
Hint.11: Choose 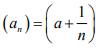 which is a Cauchy sequence in (a,b) but does not converge.
which is a Cauchy sequence in (a,b) but does not converge.
Ex.12. Let 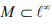 be the subspace consisting of all sequence
be the subspace consisting of all sequence 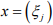 with at most finitely many nonzero terms .Find a Cauchy sequence in M which does not converge in M, so that M is not complete.
with at most finitely many nonzero terms .Find a Cauchy sequence in M which does not converge in M, so that M is not complete.
Hint.12: Choose (xn), where 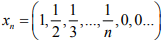 which is Cauchy in M but does not converge.
which is Cauchy in M but does not converge.
Ex.13. Show that the set X of all integers with metric d defined by d (m,n) = |m - n| is a complete metric space.
Hint.13: Consider a sequence 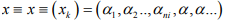
Where xk = α for k ≥ n, α is an integer.This is a Cauchy and converges to α ∈ X.
Ex.14.Let X be the set of all positive integers and d (m, n) = |m-1 - n-1|. Show that (X , d) is not complete.
Hint.14: Choose (xn) when xn = n which is Cauchy but does not converge.
Ex.15. Show that a discrete metric space is complete.
Hint.15: Constant sequence are Cauchy and convergent.
Ex.16. Let X be metric space of all real sequences 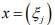 each of which has only finitely Nonzero terms, and
each of which has only finitely Nonzero terms, and 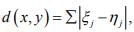 when y = (ηj). Show that
when y = (ηj). Show that 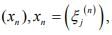
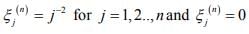
for j > n is Cauchy but does not converge.
Hint.16: For every ∈ > 0, ,there is an N s. t. for n > m >N, 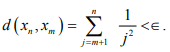
But (xn) does not converge to any 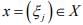 Because
Because 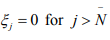 so that for n >
so that for n > 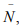
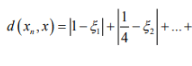
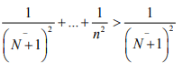 And d(xn, x) → 0 as n → ∞ is imposible.
And d(xn, x) → 0 as n → ∞ is imposible.
Ex.17. Show that,by given a example ,that a complete and an incomplete metric spaces may be Homeomorphic.
Hint.17: (Def) A homeomorphism is a continuous bijective mapping.
T: X → Y : whose inverse is continuous; the metric space X and Y are then said to be homeomorphic. e g. . A mapping T: R: → (-1 ,1) defined as 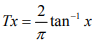 with metric d(x,y) = |x - y| on R. .Clearly T is 1-1,into & bi continuous so
with metric d(x,y) = |x - y| on R. .Clearly T is 1-1,into & bi continuous so  But R is complete while (-1,1) is an incomplete metric space.
But R is complete while (-1,1) is an incomplete metric space.
Ex.18. If (X , d) is complete, show that 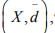 where
where 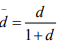 is complete.
is complete.
Hint.18: 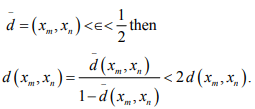
Hence if (xn) is Cauchy is 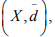 it is Cauchy in (X, d), and its limit in
it is Cauchy in (X, d), and its limit in 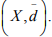
Problems on Module-II (Normed and Banach Spaces)
Ex.1. Let (X, 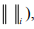 i= 1, 2, ∞ be normed spaces of all ordered pairs
i= 1, 2, ∞ be normed spaces of all ordered pairs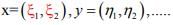 of real numbers where
of real numbers where 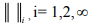 are defined as
are defined as 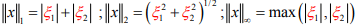
How does unit sphere in these norms look like?
Hint.1: 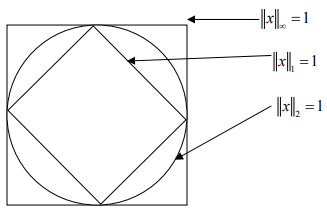
Ex.2. Show that the discrete metric on a vector space X ≠{0} can not be obtained from a norm.
Hint.2: 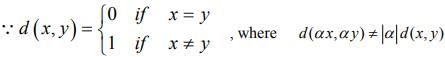
Ex.3. In l∞ ,let γ be the subset of all sequences with only finitely many non zero terms. Show that γ is a subspace of l∞ but not a closed subspace.
Hint.3: 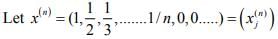 where
where 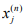 has 0 value after j>n. Clearly
has 0 value after j>n. Clearly
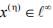 as well as x(n)∈ γ but
as well as x(n)∈ γ but 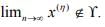
Ex.4. Give examples of subspaces of l∞ and l2 which are not closed.
Hint.4: Let γ be the subset of all sequences with only finitely many non zero terms.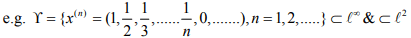
but not closed.
Ex.5. Show that a discrete metric space X consisting of infinitely many points is not compact.
Hint.5: By def. of Discrete metric, any sequences (nx) cannot have convergent subsequence as 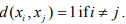
Ex.6. Give examples of compact and non compact curves in the plane R2.
Hint.6: As R2 is of finite dimension, So every closed & bounded set is compact.
Choose 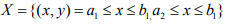 which is compact But
which is compact But 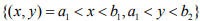 is not compact.
is not compact.
Ex.7. Show that  are locally compact.
are locally compact.
Hint.7: (def.) A metric space X is said to be locally compact if every point of X has a compact neighbourhood. Result follows (obviously).
Ex.8. Let X and Y be metric spaces. X is compact and T: X→ Y bijective and continuous. Show that T is homeomorphism.
Hint.8: Only to show T-1 is continuous i.e. Inverse image of open set under T-1 is open.
OR.
If 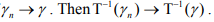 It will follow from the fact that X is compact.
It will follow from the fact that X is compact.
Ex.9. What are the domain, range and null space of T1,T2,T3 in exercise 9.
Hint.9: The domain is R2 . The ranges are the 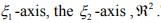 The null spaces are the
The null spaces are the 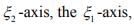 the origin.
the origin.
Ex.10. Let T : X → Y be a linear operator. Show that the image of a subspace V of X is a vector space, and so is the inverse image of a subspace W of X.
Hint.10. 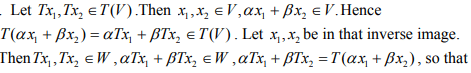
αx1 + βx2 is an element of that inverse image.
Ex.11. Let X be the vector space of all complex 2 x 2 matrices and define T: X → X by Tx=bx, where b ∈ X is fixed and bx denotes the usual product of matrices. Show that T is linear. Under what condition does T-1 exist?
Hint.11. |b| ≠ 0
Ex.12. Let T : D(T) → Y be a linear operator whose inverse exists. If {x1,x2,....,xn) is a Linearly Independant set in D(T), show that the set {Tx1,Tx2,....Txn} is L.I.
Hint.12.
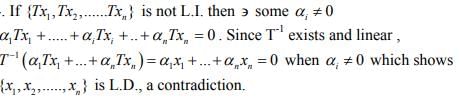
Ex.13. Consider the vector space X of all real-valued functions which are defined on R and have derivatives of all orders everywhere on R. Define T : X → X by y(t) = Tx(t) = x'(t), show that R(T) is all of X but T-1 does not exist.
Hint.13: R (T) = X since for every y ∈ X we have y = Tx, where x(t) = 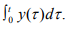 But n T-1 does not exist since Tx=0 for every constant function.
But n T-1 does not exist since Tx=0 for every constant function.
Ex.14. Let X and Y be normed spaces. Show that a linear operator T: X → Y is bounded if and only if T maps bounded sets in X into bounded set in Y.
Hint.14: Apply definition of bounded operator.
Ex.15. If T ≠ 0 is a bounded linear operator, show that for any 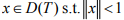 we have the strict inequality
we have the strict inequality 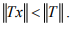
Hint.15: Since 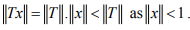
Ex.16. Find the norm of the linear functional f defined on C[-1, 1] by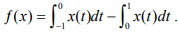
Hint.16: 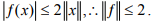 For converse, choose x(t) = -1 on [-1,1]. So
For converse, choose x(t) = -1 on [-1,1]. So 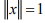
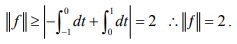
Problems on Module III (IPS/Hilbert space)
Ex.1. If x ⊥ y in an IPS X,Show that 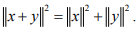
Hint.1: Use 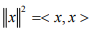 and the fact that < x y > = 0, if x ⊥ y.
and the fact that < x y > = 0, if x ⊥ y.
Ex.2. If X in exercise 1 is a real vector space, show that ,conversely, the given relation implies that x ⊥ y . Show that this may not hold if X is complex. Give examples.
Hint. 2: By Assumption,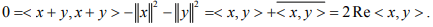
Ex.3. If an IPS X is real vector space, show that the condition 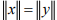 implies <x +y,x-y>= 0. What does this mean geometrically if X = R2?
implies <x +y,x-y>= 0. What does this mean geometrically if X = R2?
Hint.3: Start <x +y,x-y> = <x,x> + <y,-y> = 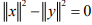 as X is real. Geometrically: If x & y are the vectors representing the sides of a parallelogram, then x+y and x-y will represent the diagonal which are⊥.
as X is real. Geometrically: If x & y are the vectors representing the sides of a parallelogram, then x+y and x-y will represent the diagonal which are⊥.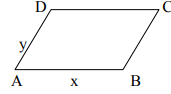
Ex.4. (Apollonius identity): For any elements x, y, z in an IPS X, show that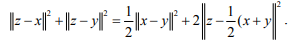
Hint 4: Use 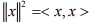 OR use parallelogram equality.
OR use parallelogram equality.
Ex.5. Let x ≠ 0 and y ≠ 0. If x ⊥ y, show that {x,y} is a Linearly Independent set.
Hint.5: Suppose 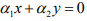 where α1,α2 are scalars. Consider
where α1,α2 are scalars. Consider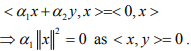
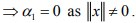 .Similarly, one can show that
.Similarly, one can show that 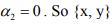 is L.I.set.
is L.I.set.
Ex.6. If in an IPS X, <x,u> = <x,v> for all x, show that u = v.
Hint.6 : Given <x,u-v> = 0. Choose x = u - v.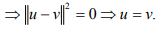
Ex.7. Let X be the vector space of all ordered pairs of complex numbers. Can we obtain the norm defined on X by 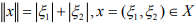 from an Inner product?
from an Inner product?
Hint. 7: No. because the vectors x= (1,1), y = (1,1) do not satisfy parallelogram equality.
Ex.8. If X is a finite dimensional vector space and (ej ) is a basis for X, show that an inner product on X is completely determined by its values 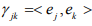 . Can we choose scalars γjk in a completely arbitrary fashion?
. Can we choose scalars γjk in a completely arbitrary fashion?
Hint.8: Use 
Open it so we get that it depends on 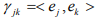
II Part: Answer:- NO. Because 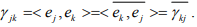
Ex.9. Show that for a sequence (xn ) in an IPS X , the conditions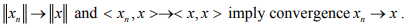
Hint.9 : We have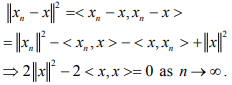
Ex.10. Show that in an IPS X,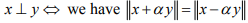 for all scalars α.
for all scalars α.
Hint.10 : From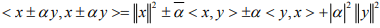 condition follows as x ⊥ y.
condition follows as x ⊥ y.
Conversely, 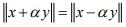
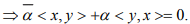
Choose α = 1 if the space is real which implies x ⊥ y.
Choose α = 1, α = i if the space is complex then we get <x,y> = 0 ⇒x ⊥ y.
Ex.11. Show that in an IPS X, 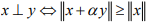 for all scalars.
for all scalars.
Hint.11 : Follows from the hint given in Ex.-10.
Ex.12. Let V be the vector space of all continuous complex valued functions on J = [a,b]. 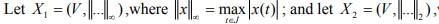
where 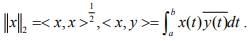 Show that the identity mapping
Show that the identity mapping 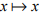 of X1 onto X2 is continuous. Is it Homeomorphism?
of X1 onto X2 is continuous. Is it Homeomorphism?
Hint.12 : Since 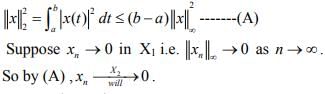
Hence I is continuous.
Part-II: Answer No. because X2 is not complete.
Ex.13. Let H be a Hilbert space, 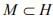 a convex subset, and (xn) is a sequence in M such that
a convex subset, and (xn) is a sequence in M such that 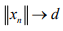 , where
, where 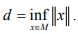 Show that (xn) converges in H.
Show that (xn) converges in H.
Hint.13 : (xn) is Cauchy, since from the assumption and the parallelogram equality, we have,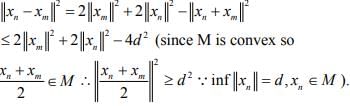
Ex.14. If (ek) is an orthonormal sequence in an IPS X, and x ∈ X, show that x-y with y given by 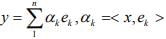 is orthogonal to the subspace
is orthogonal to the subspace 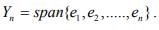
Hint.14 :
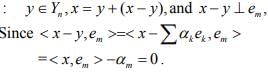
Ex.15. Let (ek) be any orthonormal sequence in an IPS X. Show that for any , x y ∈ X, 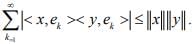
Hint.15: Use Cauchy Schwaz’s Inequality & Bessel’s Inequality, we get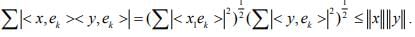
Ex.-16. Show that in a Hilbert Space H,convergence of 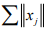 implies convergence of
implies convergence of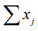
Hint.16 : Let 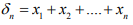
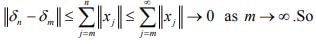
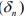 is a Cauchy. Since H is complete, hence
is a Cauchy. Since H is complete, hence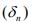 will converge.
will converge.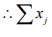 converge in H.
converge in H.
Problems On Module IV (On Fundamental theorems)
Ex.1. Let 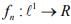 be a sequence of bounded linear functionals defined as
be a sequence of bounded linear functionals defined as 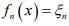 where
where 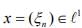 . show that (fn)converge strongly to 0 but not uniformly.
. show that (fn)converge strongly to 0 but not uniformly.
Hint.1 : Since 
ie 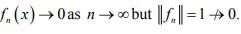
Ex.2. Let 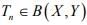 where X is a Banach space and Y a normed space. If (Tn) is strongly convergent with limit T, then
where X is a Banach space and Y a normed space. If (Tn) is strongly convergent with limit T, then 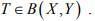
Hint.2 T linear follows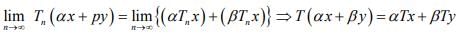
T is bounded :- Since 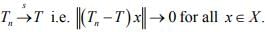
So (Tnx) is bounded for every x.Since X is complete, so  is bounded by uniform bounded ness theorem. Hence
is bounded by uniform bounded ness theorem. Hence 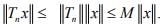 Taking limit ⇒ T is bounded.
Taking limit ⇒ T is bounded.
Ex.3. If 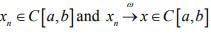 . Show that (xn) is point wise convergent on [a,b].
. Show that (xn) is point wise convergent on [a,b].
Hint .3 : A bounded linear functional on 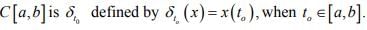
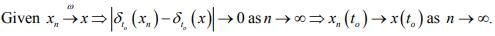
Ex.4. If 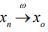 in a normed space X. Show that
in a normed space X. Show that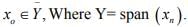
Hint.4 : Use Lemma:- ‘’Let Y be a proper closed sub-space of a normed space X and let 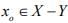 be arbitrary point and
be arbitrary point and 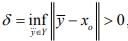 then there exists an
then there exists an 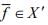 , dual of X such that
, dual of X such that 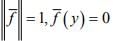 for all y ∈ Y and
for all y ∈ Y and 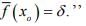
suppose 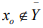 which is a closed sub space of X. so by the above result ,
which is a closed sub space of X. so by the above result ,
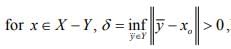 hence there exists
hence there exists 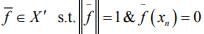
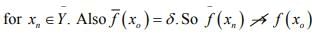
which is a contradiction that
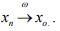
Ex.5. Let Tn = Sn, where the operator 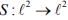 is defined by S
is defined by S 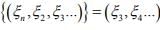 Find a bound for
Find a bound for 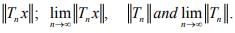
Hint.5 : 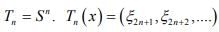
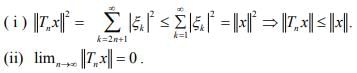
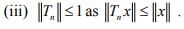 For converse, choose x =
For converse, choose x =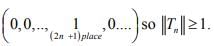
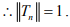
(iv) 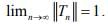
Ex.6. Let X be a Banach space, Y a normed space and 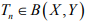 such that (Tnx) is Cauchy in Y for every x ∈ X. .show that
such that (Tnx) is Cauchy in Y for every x ∈ X. .show that 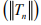 is bounded.
is bounded.
Hint. 6 : Since (Tnx)is Cauchy in Y for every x, so it is bounded for each x ∈ X. Hence by uniform bounded ness theorem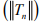 is bounded.
is bounded.
Ex.7. If (xn) in a Banach space X is such that 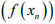 is bounded for all
is bounded for all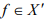 .Show that
.Show that 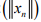 is bounded.
is bounded.
Hint.7 : Suppose 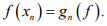 Then
Then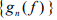 is bounded for every
is bounded for every 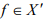 . So by uniform bounded ness theorem
. So by uniform bounded ness theorem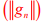 is bounded and
is bounded and 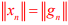 .
.
Ex.8. If a normed space X is reflexive, Show that X' is reflexive.
Hint. 8 : Let 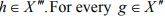 there is an x ∈ X such that g = Cx since X is reflexive. Hence h(g) = h (Cx) = f(x) defines a bounded linear functional f on X and
there is an x ∈ X such that g = Cx since X is reflexive. Hence h(g) = h (Cx) = f(x) defines a bounded linear functional f on X and 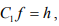 where
where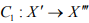 is the canonical mapping. Hence C1 is surjective, so that X' is reflexive.
is the canonical mapping. Hence C1 is surjective, so that X' is reflexive.
Ex.9. If x0 in a normed space X is such that 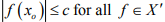 of norm1. show that
of norm1. show that 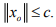
Hint. 9 : suppose 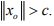 Then by Lemma: Let X be a normed space and let
Then by Lemma: Let X be a normed space and let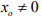 be any elementof X. Then there exist a bounded linear functional
be any elementof X. Then there exist a bounded linear functional 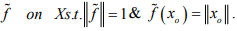
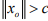 would imply the existence of an
would imply the existence of an 
Ex.10. Let Y be a closed sub space of a normed space X such that every f ∈ X which is zero every where on Y is zero every where on the whole space X. Show that Y = X
Hint. 10 : If , Y ≠ X there is an 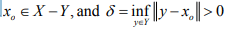 since Y is closed.
since Y is closed.
Use the Lemma as given in Ex 4 ( Hint ).
By this Lemma, there is on 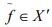 which is zero on Y but not zero at x0, which contradicts our assumption.
which is zero on Y but not zero at x0, which contradicts our assumption.
Ex.11. Prove that 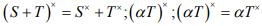 Where Tx is the adjoint operator of T.
Where Tx is the adjoint operator of T.
Hint. 11 : 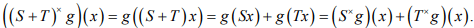
Similarly others.
Ex.12. Prove (ST)x = TxSx
Hint. 12 : 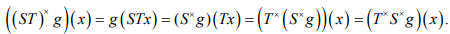
Ex.13. Show that (Tn)x = (Tx)n.
Hint. 13 : Follows from Induction.
Ex.14. Of what category is the set of all rational number (a) in 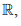 , ( b ) in itself, (Taken usual metric)
, ( b ) in itself, (Taken usual metric)
Hint 14 : (a) first (b) first.
Ex.15. Find all rare sets in a discrete metric space X.
Hint.15 : 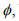 because every subset of X is open
because every subset of X is open
Ex.16. Show that a subset M of a metric space X is rare in X if and only if is 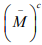 is dense in X.
is dense in X.
Hint. 16 : The closure of 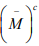 is all of X if and if
is all of X if and if 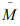 has no interior points, So that every
has no interior points, So that every 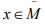 is a point of accumulation of
is a point of accumulation of 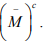
Ex.17. Show that completeness of X is essential in uniform bounded ness theorem and cannot be omitted.
Hint.17 : Consider the sub space 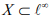 consisting of all
consisting of all 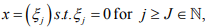 where J depends on x, and let Tn be defined by
where J depends on x, and let Tn be defined by 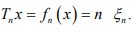 Clearly
Clearly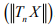 is bounded
is bounded 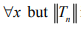 is not bounded.
is not bounded.
|
2 videos|45 docs|4 tests
|
FAQs on Question For Practice With Solutions:- Normed Linear Spaces - Additional Topics for IIT JAM Mathematics
| 1. What is a normed linear space? |  |
| 2. What are some examples of normed linear spaces? |  |
| 3. What is the difference between a normed linear space and a metric space? |  |
| 4. How is the norm of a vector calculated in a normed linear space? |  |
| 5. What are some applications of normed linear spaces in mathematics? |  |
















