Section Formula in 3D | Additional Topics for IIT JAM Mathematics PDF Download
Coordinates in 3D
Just like in two dimensions, you can give coordinates to a point in 3D. The three dimensions are the x-axis, y-axis, and z-axis. A point in three dimensions will have coordinates (x, y, z). This ordered tuple has its application in our day to day life.
Take an example of the cricket match. The ball in the sky can be positioned by its coordinates. The position of the submarines, airplanes etc. are all given by its coordinates in 3D.
Section Formulas in 3D
Suppose you draw a line in a white sheet and you put a point anywhere either on the line or not on the line. This point cuts the line segment into two parts. These parts are maybe in some ratio with each other.
By using this ratio we can find the coordinates of the point in a plane in three dimensions. Section formulas in 3D is similar to the section formulas in two dimensions.
Section Formula (Dividing Internally)
Here we will understand how to find the section formula or the coordinates of a point lying on a line. Let AB be a line segment with coordinates (x1, y1, z1) & (x2, y2, z2) respectively. A point C (x, y, z) divides PR in the ratio m:n internally.
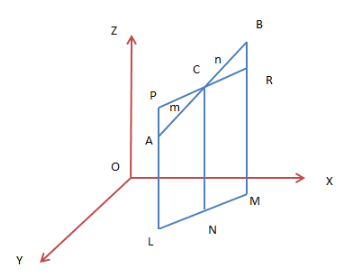
AL, CN, BM be the perpendiculars on XY-plane. These perpendiculars are parallel with each other. Let L, N, M form collinear points of the line LM. From the point C, we draw a line PR || LM. It is notable that PL intersect the line AL externally and RM intersect BM internally. The triangles APC and BRC are similar. Therefore,
m ⁄ n = AC ⁄ BC = PA ⁄ BR = (PL − AL) ⁄ (BM – RM) = (CN – AL) ⁄ (BM – CN) = (z – z1) ⁄ (z2 – z)
Solving both sides, we have z = (mz2 + nz1) ⁄ (m+n). Similarly, we have y = (my2 + ny1) ⁄ (m+n) and x = (mx2 + nx1) ⁄ (m+n). The coordinates of the point C which divides AB internally at the ratio m:n are
((mx2 + nx1) ⁄ (m + n), (my2 + ny1) ⁄ (m + n), (mz2 + nz1) ⁄ (m + n))
Section Formula (Dividing Externally)
Let AB be a line segment with coordinates (x1, y1, z1) & (x2, y2, z2) respectively. A point C (x, y, z) divides PR in the ratio m:n externally. The coordinates of C are given by replacing n by −n:
((mx2 − nx1) ⁄ (m − n), (my2 − ny1) ⁄ (m − n), (mz2 − nz1) ⁄ (m − n)).
Solved Examples for You
Problem: What are the coordinates of a point which divides a line segment into equal halves?
Solution: Let AB be a line segment such that A (x1, y1, z1) and B (x2, y2, z2). C is the mid-point of the line segment AB.
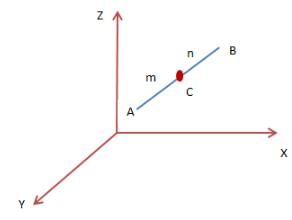
Here, m = n = 1. Putting in the section formula we have, C (x, y); x = (x1 + x2) ⁄ 2, y = (y1 + y2) ⁄ 2.
Problem: Use the section formula in 3D and find the coordinates of the points L and M which divides the line segment AB internally and externally both at the ratio 3:5? The coordinates of A are (2, 4, 1) and B are (1, 3, 2).
Solution: The coordinates of L (dividing AB internally), x = (3×1 + 5×2) ⁄ (3 + 5) = (3 + 10) ⁄ 8 = 13⁄8, y = (3×3 + 5×4) ⁄ (3 + 5) = (9 + 20) ⁄ 8 = 29⁄8, z = (3×2 + 5×1) ⁄ (3 + 5) = (6 + 5) ⁄ 8 = 11⁄8. The coordinates are (13⁄8, 29⁄8, 11⁄8).
Coordinates of L (dividing AB externally), x = (3×1 − 5×2) ⁄ (3 − 5) = (3 − 10) ⁄ −2 = 7⁄ 2, y = (3×3 − 5×4) ⁄ (3 − 5) = (9 − 20) ⁄ −2 = 11⁄ 2, z = (3×2 − 5×1) ⁄ (3 − 5) = (6 − 5) ⁄ −2 = −1⁄ 2. The coordinates are (7⁄2, 11⁄2, −1⁄2).
|
2 videos|44 docs|4 tests
|
FAQs on Section Formula in 3D - Additional Topics for IIT JAM Mathematics
| 1. What is the section formula in 3D mathematics? |  |
| 2. How is the section formula derived in 3D mathematics? |  |
| 3. What is the significance of the section formula in 3D mathematics? |  |
| 4. Can the section formula be applied to any line segment in 3D mathematics? |  |
| 5. Are there any limitations or restrictions when using the section formula in 3D mathematics? |  |



















