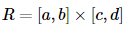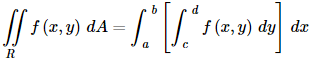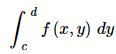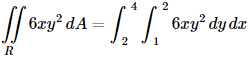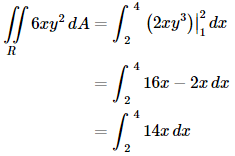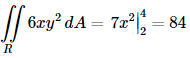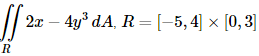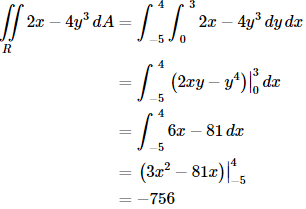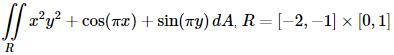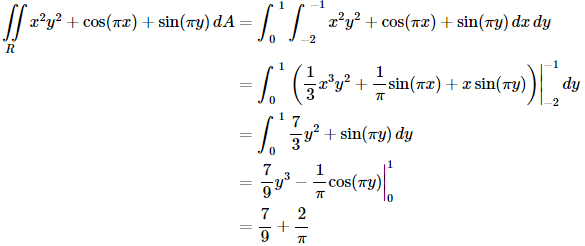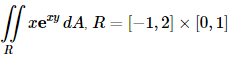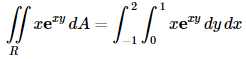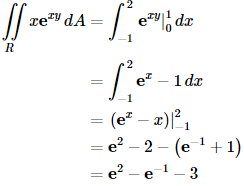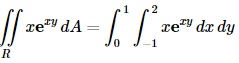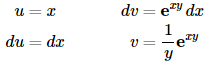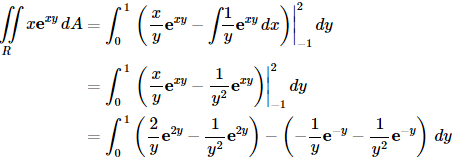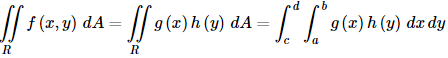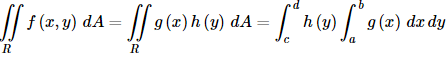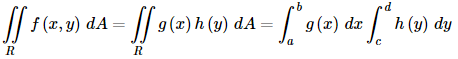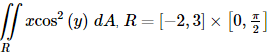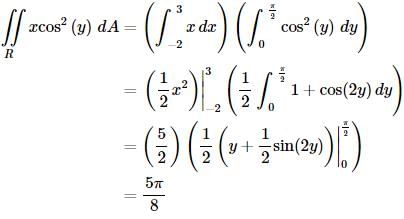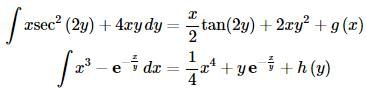In the previous section we gave the definition of the double integral. However, just like with the definition of a single integral the definition is very difficult to use in practice and so we need to start looking into how we actually compute double integrals. We will continue to assume that we are integrating over the rectangle
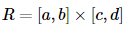
We will look at more general regions in the next section.
The following theorem tells us how to compute a double integral over a rectangle.
Fubini’s Theorem
If f ( x , y ) is continuous on R = [ a , b ] × [ c , d ] then,
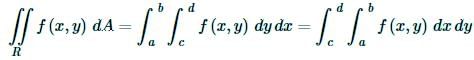
These integrals are called iterated integrals.
Note that there are in fact two ways of computing a double integral over a rectangle and also notice that the inner differential matches up with the limits on the inner integral and similarly for the outer differential and limits. In other words, if the inner differential is dy then the limits on the inner integral must be y limits of integration and if the outer differential is dy then the limits on the outer integral must be y limits of integration. Now, on some level this is just notation and doesn’t really tell us how to compute the double integral. Let’s just take the first possibility above and change the notation a little.
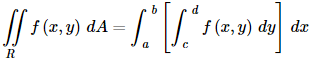
We will compute the double integral by first computing
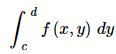
and we compute this by holding x constant and integrating with respect to y as if this were a single integral. This will give a function involving only x ’s which we can in turn integrate. We’ve done a similar process with partial derivatives. To take the derivative of a function with respect to y we treated the x ’s as constants and differentiated with respect to y as if it was a function of a single variable. Double integrals work in the same manner. We think of all the x ’s as constants and integrate with respect to y or we think of all y ’s as constants and integrate with respect to x . Let’s take a look at some examples.
Example 1 Compute each of the following double integrals over the indicated rectangles.
(a)

(a) It doesn’t matter which variable we integrate with respect to first, we will get the same answer regardless of the order of integration. To prove that let’s work this one with each order to make sure that we do get the same answer. Solution 1 In this case we will integrate with respect to y first. So, the iterated integral that we need to compute is,
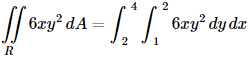
When setting these up make sure the limits match up to the differentials. Since the d y is the inner differential (i.e. we are integrating with respect to y first) the inner integral needs to have y limits. To compute this we will do the inner integral first and we typically keep the outer integral around as follows,
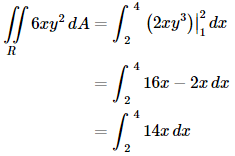
Remember that we treat the x as a constant when doing the first integral and we don’t do any integration with it yet. Now, we have a normal single integral so let’s finish the integral by computing this.
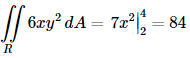
Solution 2 In this case we’ll integrate with respect to x first and then y. Here is the work for this solution.

Sure enough the same answer as the first solution.
So, remember that we can do the integration in any order.
(b)
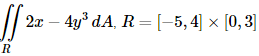
(b) For this integral we’ll integrate with respect to y first.
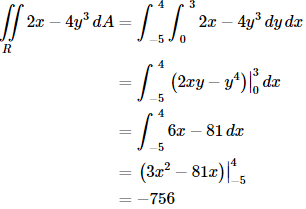
Remember that when integrating with respect to y all x ’s are treated as constants and so as far as the inner integral is concerned the 2x is a constant and we know that when we integrate constants with respect to y we just tack on a y and so we get 2xy from the first term.
(c) 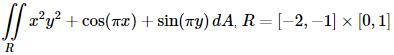
In this case we’ll integrate with respect to x first.
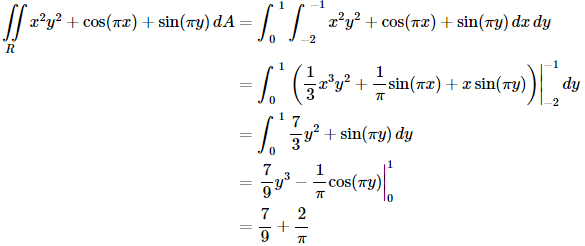
(d) 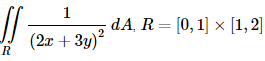
(d) In this case because the limits for x are kind of nice (i.e. they are zero and one which are often nice for evaluation) let’s integrate with respect to x first. We’ll also rewrite the integrand to help with the first integration.
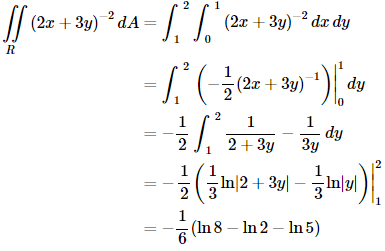
(e)
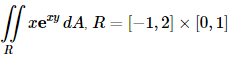
(e) Now, while we can technically integrate with respect to either variable first sometimes one way is significantly easier than the other way. In this case it will be significantly easier to integrate with respect to y first as we will see.
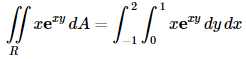
The y integration can be done with the quick substitution,
u=xy, du=xdy
which gives
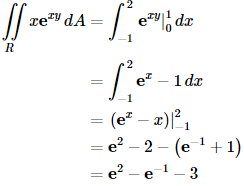
So, not too bad of an integral there provided you get the substitution. Now let’s see what would happen if we had integrated with respect to x first.
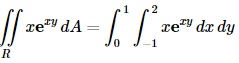
In order to do this we would have to use integration by parts as follows,
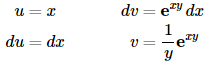
The integral is then,
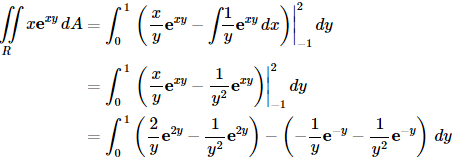
We’re not even going to continue here as these are very difficult, if not impossible, integrals to do.
As we saw in the previous set of examples we can do the integral in either direction. However, sometimes one direction of integration is significantly easier than the other so make sure that you think about which one you should do first before actually doing the integral. The next topic of this section is a quick fact that can be used to make some iterated integrals somewhat easier to compute on occasion. There is a nice special case of this kind of integral. First, let’s assume that f(x , y) = g(x) h(y) and let’s also assume we are integrating over a rectangle given by R=[a , b] × [c , d] . Then, the integral becomes,
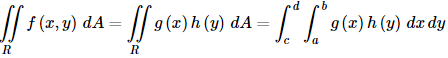
Note that it doesn’t matter in this case which variable we integrate first as either order will arrive at the same result with the same work. Next, notice that because the inner integral is with respect to x and h ( y ) is a function only of y it can be considered a “constant” as far as the x integration is concerned (changing x will not affect the value of y !) and because it is also times g ( x ) we can factor the h ( y ) out of the inner integral. Doing this gives,
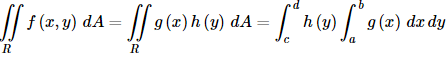
Now, ∫ b a g ( x ) d x is a standard Calculus I definite integral and we know that its value is just a constant. Therefore, it can be factored out of the y integration to get,
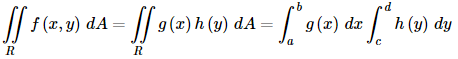
In other words, if we can break up the function into a function only of x times a function of only y then we can do the two integrals individually and multiply them together. Here is a quick summary of this idea.
Fact
If f ( x , y ) = g ( x ) h ( y ) and we are integrating over the rectangle R = [ a , b ] × [ c , d ] then,
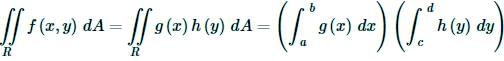
Let’s do a quick example using this integral.
Example 2: Evaluate 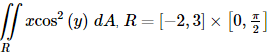
Solution: Since the integrand is a function of x times a function of y we can use the fact.
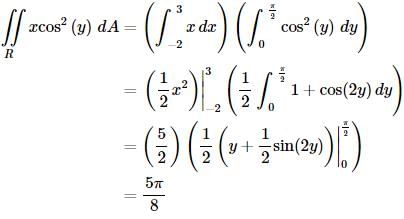
We have one more topic to discuss in this section. This topic really doesn’t have anything to do with iterated integrals, but this is as good a place as any to put it and there are liable to be some questions about it at this point as well so this is as good a place as any.
What we want to do is discuss single indefinite integrals of a function of two variables. In other words, we want to look at integrals like the following.

From Calculus I we know that these integrals are asking what function that we differentiated to get the integrand. However, in this case we need to pay attention to the differential ( dy or dx ) in the integral, because that will change things a little. In the case of the first integral we are asking what function we differentiated with respect to y to get the integrand while in the second integral we’re asking what function differentiated with respect to x to get the integrand. For the most part answering these questions isn’t that difficult. The important issue is how we deal with the constant of integration. Here are the integrals.
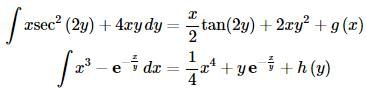
Notice that the “constants” of integration are now functions of the opposite variable. In the first integral we are differentiating with respect to y and we know that any function involving only x ’s will differentiate to zero and so when integrating with respect to y we need to acknowledge that there may have been a function of only x ’s in the function and so the “constant” of integration is a function of x . Likewise, in the second integral, the “constant” of integration must be a function of y since we are integrating with respect to x . Again, remember if we differentiate the answer with respect to x then any function of only y ’s will differentiate to zero.