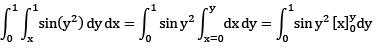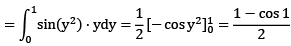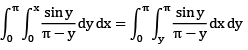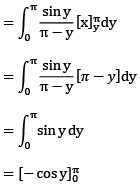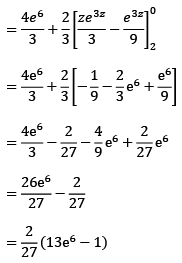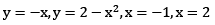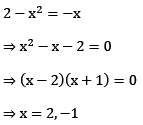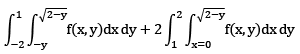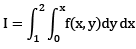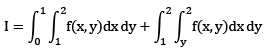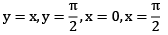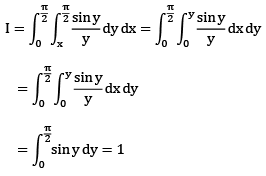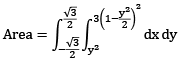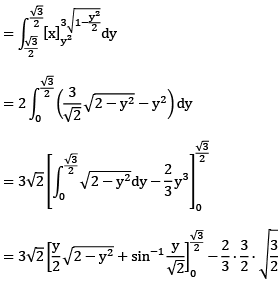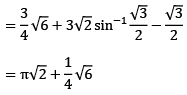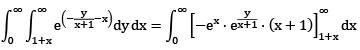Doc - MCQ:- Calculus, Integrals, Multiple, integrals | Topic-wise Tests & Solved Examples for Mathematics PDF Download
Que 1: 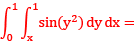
Sol: Region bounded by
x = 0, x = 1 and y = x, y = 1
Now we evaluate the integral by hanging the order of integral
Que 2: The value of the double integral 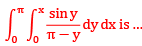
Sol: Region of integration is bounded y=0, y = x and x = 0, x = π
changing the order of integration
= 2
Que :-3 Evaluate 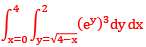
Sol:
Que 4:- Change the order of integration in the double integral 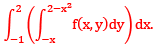
Sol: Domain of integration is bounded by the following curves
point of intersection of the curve y =2 - x2 and y = -x we get when
So (-1,1 ) and (2,-2 ) are the points of intersection.
Now the given integral modify by changing the order of integration we get
Que 5:- Changing the order of integration of 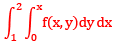
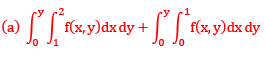
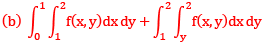
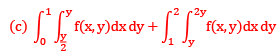
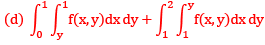
Sol:
The region of integration is bounded by y = 0, y = x, x = 1, x = 2 after changing the order the integration changes to
Que 6:- Let D the triangle bounded by the y-axis the line 2y = π. Then the value of the integral 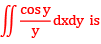
(a) 1/2
(b) 1
(c) 3/2
(d) 2
Sol:
Que 7: Change the order of integration in the integral 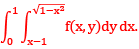
Sol:
Que 8:- Let I = 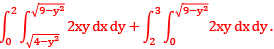 Then using the transformation x = rcosθ, y = rsinθ, integral is equal to
Then using the transformation x = rcosθ, y = rsinθ, integral is equal to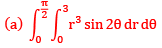
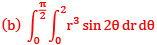
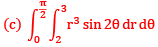
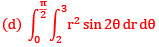
Sol:
Que 9: Evaluate integral 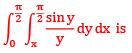
(a) 0
(b) 1/2
(c) 1
(d)2
Sol: Region of integration is bounded by curves
changing the order
Que10:- The value of  equals
equals
(a) π/4
(b) 1/2π
(c) 1/4
(d) 1/2
Sol: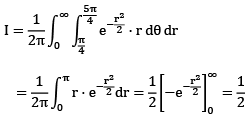
Que 11:
(a) Find in the area of the smaller of the two regions enclose between 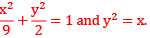
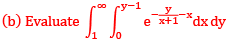
Sol:
Sol (b)
The region of integration is bounded by x = 0, x = y, y = 1, y = ∞ and shown in figure changing the order
Que12:- Let f ,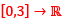 be a continuous function with
be a continuous function with 
Sol:
Que13:- By changing the order of integration, the integral 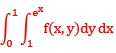 can be expressed as
can be expressed as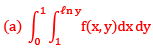
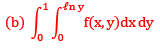
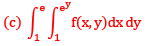

Sol:
|
27 docs|150 tests
|
FAQs on Doc - MCQ:- Calculus, Integrals, Multiple, integrals - Topic-wise Tests & Solved Examples for Mathematics
| 1. What is the fundamental theorem of calculus and how does it connect differentiation and integration? |  |
| 2. How do you evaluate a definite integral using the substitution method? |  |
| 3. What are multiple integrals and how are they applied in real-world scenarios? |  |
| 4. Can you explain the properties of definite integrals? |  |
| 5. What is the difference between an indefinite integral and a definite integral? |  |