Homomorphism, Group Theory | Algebra - Mathematics PDF Download
Homomorphisms are the maps between algebraic objects. There are two main types: group homomorphisms and ring homomorphisms. (Other examples include vector spacehomomorphisms, which are generally called linear maps, as well as homomorphisms of modules and homomorphisms of algebras.)
Generally speaking, a homomorphism between two algebraic objects A, B is a function f : A → B which preserves the algebraic structure on A and B That is, if elements in A satisfy some algebraic equation involving addition or multiplication, their images in B satisfy the same algebraic equation. The details of the definitions of homomorphisms in various contexts depend on the algebraic structures of A and B.
EXAMPLE If the operations on A and B are both addition, then the homomorphism condition is |
A bijective homomorphism is called an isomorphism. An isomorphism between two algebraic objects and identifies them with each other; they are, in an algebraic sense, the same object (possibly written in two different ways). The most common use of homomorphisms in abstract algebra is via the three so-called isomorphism theorems, which allow for the identification of certain quotient objects with certain other subobjects (subgroups, subrings, etc.)
The study of the interplay between algebraic objects is fundamental in the study of algebra. The existence and properties of homomorphisms from one algebraic object to another give a rich depth of information about the objects and their relationship. Many important concepts in abstract algebra, such as
the integers modulo n
a prime ideal in a ring
the sign of a permutation,
can be naturally considered as (respectively) the image of a homomorphism, the kernel of a homomorphism, or the homomorphism itself.
Definitions and Examples
Let A and B be groups, with operations given by ºA and ºB respectively. A group homomorphism f : A → B is a function f such that 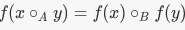 for all x,y ∈ A. for all x,y ∈ A. |
DEFINATION Let R and S be rings, with operations + and . (this is a slight abuse of notation, but the formulas below are more unwieldy with subscripts on the operations). A ring homomorphism f : R → S is a function f such that
(In this wiki, "ring" means "ring with unity"; a homomorphism of rings is defined in the same way, but without the third condition.) |
In both cases, a homomorphism is called an isomorphism if it is bijective.
EXAMPLE Show that if f : R → S is a ring homomorphism, f(0R) = os. Note that |
EXAMPLE 1. For any groups G and H, there is a trivial homomorphis |
Kernel and Image
Any homomorphism f : A → B has two objects associated to it: the kernel, which is a subset of A, and the image, which is a subset of B.
DEFINATION
|
For further exploration of the kernel in the setting of vector spaces, see the wiki.
The kernel of a homomorphism is an important object, in both group and ring theory. The following theorem identifies what kind of object it is:
EXAMPLE Continuing the six examples above: 1. If |
Properties of Homomorphisms
- Composition: The composition of homomorphisms is a homomorphism. That is, if
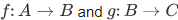 are homomorphisms, then
are homomorphisms, then 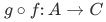 is a homomorphism as well.
is a homomorphism as well. - Isomorphisms: If f is an isomorphism, which is a bijective homomorphism, then
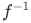 is also a homomorphism. (Compare with homeomorphism, a similar concept in topology, which is a continuous function with a continuous inverse; a bijective continuous function does not necessarily have a continuous inverse.)
is also a homomorphism. (Compare with homeomorphism, a similar concept in topology, which is a continuous function with a continuous inverse; a bijective continuous function does not necessarily have a continuous inverse.) - Injectivity and the kernel: A group homomorphism f is injective if and only if its kernel ker(f) equals {1}, where denotes the identity element of the domain. A ring homomorphism is injective if and only if its kernel equals {0} where 0 denotes the additive identity of the domain.
- Field homomorphisms: If R is a field and S is not the zero ring, then any homomorphism
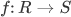 is injective. (Proof: the kernel is an ideal, and the only ideals in a field are the entire field and the zero ideal. Since
is injective. (Proof: the kernel is an ideal, and the only ideals in a field are the entire field and the zero ideal. Since 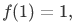 it must be the latter.)
it must be the latter.)
|
181 videos|58 docs
|
FAQs on Homomorphism, Group Theory - Algebra - Mathematics
| 1. What is a homomorphism in group theory? |  |
| 2. How does a homomorphism relate to the concept of isomorphism? |  |
| 3. What are the applications of homomorphisms in mathematics? |  |
| 4. Can you provide an example of a homomorphism in group theory? |  |
| 5. How is the concept of homomorphism useful in solving mathematical problems? |  |

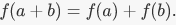 If A and B are both rings, with addition and multiplication, there is also a multiplicative condition:
If A and B are both rings, with addition and multiplication, there is also a multiplicative condition: 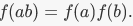
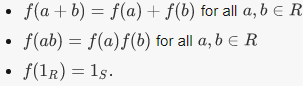
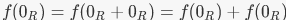 by the homomorphism property. Since f(0R) has an additive inverse in S, we can add it to both sides of this equation to get 0S = f(0R).
by the homomorphism property. Since f(0R) has an additive inverse in S, we can add it to both sides of this equation to get 0S = f(0R).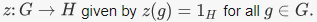 2. Let be a positive integer. The function
2. Let be a positive integer. The function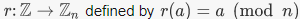 is a ring homomorphism (and as such, it is a homomorphism of additive groups).3. Define
is a ring homomorphism (and as such, it is a homomorphism of additive groups).3. Define 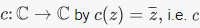 is complex conjugation. Then c is a homomorphism from C to itself. It is clearly a bijection, so it is in fact an isomorphism from C to itself.4. Let R be a subring of S, and pick
is complex conjugation. Then c is a homomorphism from C to itself. It is clearly a bijection, so it is in fact an isomorphism from C to itself.4. Let R be a subring of S, and pick 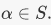 Then there is an evaluation homomorphism
Then there is an evaluation homomorphism 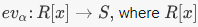 is the ring of polynomials with coefficients in R.It is given by
is the ring of polynomials with coefficients in R.It is given by 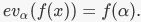 5. The map
5. The map 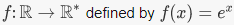 is a group homomorphism. Note that R is an additive group and R* the set of nonzero real numbers, is a multiplicative group. The verification that f is a group homomorphism is precisely the law of exponents:
is a group homomorphism. Note that R is an additive group and R* the set of nonzero real numbers, is a multiplicative group. The verification that f is a group homomorphism is precisely the law of exponents: 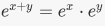 6. Let Sn be the symmetric group on n letters. There is a unique nontrivial group homomorphism
6. Let Sn be the symmetric group on n letters. There is a unique nontrivial group homomorphism 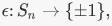 the latter being a group under multiplication. The value
the latter being a group under multiplication. The value 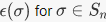 is called the sign of σ, and is important in many applications, including one definition of the
is called the sign of σ, and is important in many applications, including one definition of the 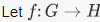 be a group homomorphism. The kernel of f, ker (f), is the subset of G consisting of elements G such that
be a group homomorphism. The kernel of f, ker (f), is the subset of G consisting of elements G such that 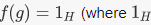 is the group identity element).
is the group identity element).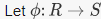 be a ring homomorphism. The kernel of
be a ring homomorphism. The kernel of  is the subset of R consisting of elements R such that
is the subset of R consisting of elements R such that 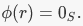
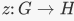 is the trivial homomorphism, then ker
is the trivial homomorphism, then ker 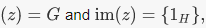 the trivial subgroup of H2. The kernel of reduction mod n is the ideal
the trivial subgroup of H2. The kernel of reduction mod n is the ideal 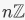 consisting of multiples of n. The image is all of Zn; reduction mod n is surjective.
consisting of multiples of n. The image is all of Zn; reduction mod n is surjective.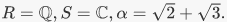 Which polynomials with rational coefficients vanish on
Which polynomials with rational coefficients vanish on 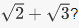 (See the algebraic number theory wiki for an answer.)The image of evaluation at α is a ring called R[α], which is a subring of S consisting of polynomials in α with coefficients in R.5. The kernel of exponentiation is the set of elements which map to the identity element of R*, which is 1 So the kernel is {0}. And the image of exponentiation is the subgroup
(See the algebraic number theory wiki for an answer.)The image of evaluation at α is a ring called R[α], which is a subring of S consisting of polynomials in α with coefficients in R.5. The kernel of exponentiation is the set of elements which map to the identity element of R*, which is 1 So the kernel is {0}. And the image of exponentiation is the subgroup 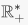 of positive real numbers.6. The kernel of the sign homomorphism is known as the alternating group An. It is an important subgroup of Sn which furnishes examples of simple groups for
of positive real numbers.6. The kernel of the sign homomorphism is known as the alternating group An. It is an important subgroup of Sn which furnishes examples of simple groups for 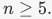 The image of the sign homomorphism is
The image of the sign homomorphism is 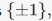 since the sign is a nontrivial map, so it takes on both
since the sign is a nontrivial map, so it takes on both 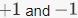 for certain permutations.
for certain permutations.














