Unique Factorization Domain | Algebra - Mathematics PDF Download
4.1 Unique Factorization Domains (UFDs)
Throughout this section R will denote an integral domain (i.e. a commutative ring with identity containing no zero-divisors). Recall that a unit of R is an element that has an inverse with respect to multiplication. If a is any element of R and u is a unit, we can write
a = u(u -1a):
This is not considered to be a proper factorization of a. For example we do not consider 5 = 1(5) or 5 = (-1)(-5) to be proper factorizations of 5 in Z. We do not consider to be a proper factorization of x2 + 2 in Q[x].

Definition 4.1.1 An element a in an integral domain R is called irreducible if it is not zero or a unit, and if whenever a is written as the product of two elements of R, one of these is a unit.
An element p of an integral domain R is cal led prime if p is not zero or a unit, and whenever p divides ab for elements a; b of R, either p divides a or p divides b.
Note
1. Elements r and s are called associates of each other if s = ur for a unit u of R. So a ∈ R irreducible if it can only be factorized as the product of a unit and one of its own associates.
2. If R is an integral domain, every prime element of R is irreducible. To see this let p ∈ R be prime and suppose that p = rs is a factorisation of p in R. Then since p divides rs, either p divides r or p|s. There is no loss of generality in assuming p divides r. Then r = pa for some element a of R, and p = rs so p = pas. Then p pas = 0 so p(1 - as) = 0 in R. Thus as = 1 since R is an integral domain and p ≠ 0. Then s is a unit and p = rs is not a proper factorisation of p. Hence p is irreducible in R.
It is not true that every irreducible element of an integral domain must be prime, as we will shortly see.
Examples:
1. In Z the units are 1 and 1 and each non-zero non-unit element has two associates, namely itself and its negative. SO 5 and -5 are associates, 6 and -6 are associates, and so on. The irreducible elements of Z are p and -p, for p prime.
2. In Q[x], the units are the non-zero constant polynomials. The associates of a non-zero non-constant polynomial f (x) are the polynomials of the form af (x) where a ∈ Qx .
So x2 + 2 is associate to  .
.
3. In Z the irreducible elements are the integers p and -p where p is a prime numbers. The prime elements of Z are exactly the irreducible elements - the prime numbers and their negatives.
Definition 4.1.2 An integral domain R is a unique factorization domain if the following conditions hold for each element a of R that is neither zero nor a unit.
1. a can be written as the product of a nite number of irreducible elements of R.
2. This can be done in an essential ly unique way. If a = p1 p2 ... pr and a = q1 q2 ... qs are two expressions for a as a product of irreducible elements, then s = r and q1 ... qs can be reordered so that for each i, qi is an associate of pi.
Example 4.1.3 Z is a UFD.
(This is the Fundamental Theorem of Arithmetic).
Example 4.1.4 Let  denote the set of complex numbers of the form
denote the set of complex numbers of the form  where a and b are integers and
where a and b are integers and  denotes the complex number
denotes the complex number  . We will show that
. We will show that  is not a UFD (it is easily shown to be a ring under the usual addition and multiplication of complex numbers).
is not a UFD (it is easily shown to be a ring under the usual addition and multiplication of complex numbers).
Claim:  is not a UFD.
is not a UFD.
The proof if this claim will involve a number of steps.
1. We define a function  denotes the complex conjugate of a. thus
denotes the complex conjugate of a. thus
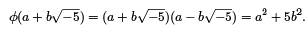


So φ is multiplicative.
2. Suppose α is a unit of  and let β be its inverse.
and let β be its inverse. 
 are positive integers this means
are positive integers this means  So φ(α) = 1 whenever α is a unit.
So φ(α) = 1 whenever α is a unit.
On the other hand  for integers a and b which means b = 0 and a = ±1. So the only units of Z[
for integers a and b which means b = 0 and a = ±1. So the only units of Z[ ] are 1 and -1.
] are 1 and -1.
3. 3. Suppose φ(α) = 9 for some a ∈ Z[ ], If a is not irreducible in Z[
], If a is not irreducible in Z[ ] then it factorizes as α1α2 where a\ and a2 are non-units. Then we must have
] then it factorizes as α1α2 where a\ and a2 are non-units. Then we must have

Now this would means 3 = c2 + 5d2 for integers c and d which is impossible. So if φ(α) = 9 then α is irreducible in Z[ ].
].
4. Now 9 = 3 x 3 and 9 = (2 +  )(2 -
)(2 - ) in Z[
) in Z[ ]. The elements (3, 2 +
]. The elements (3, 2 +  ) and 2 -
) and 2 -  ) are all irreducible in Z[
) are all irreducible in Z[ ] by item 3. above. Furthermore 3 is not an associate of either 2 +
] by item 3. above. Furthermore 3 is not an associate of either 2 +  or 2 -
or 2 - as the only units in Z[
as the only units in Z[ ] are 1 and -1. We conclude that the factorizations of 9 above are genuinely different, and Z[
] are 1 and -1. We conclude that the factorizations of 9 above are genuinely different, and Z[ ] is not a UFD.
] is not a UFD.
Note that 3 is an example of an element of Z[ ] that is irreducible but not prime.
] that is irreducible but not prime.
Remark: The ring Z[i] = {a + bi : a; b ∈ Z} is a UFD.
Theorem 4 .1.5 Let F be a eld. Then the polynomial ring F [x] is a UFD.
Proof: We need to show that every non-zero non-unit in F[x] can be written as a product of irreducible polynomials in a manner that is unique up to order and associates.
So let f (x) be a polynomial of degree n > 1 in F [x]. If f (x) is irreducible there is nothing to do. If not then f (x) = g(x)h(x) where g(x) and h(x) both have degree less than n. If
g(x) or h(x) is reducible further factorization is possible; the process ends after at most n steps with an expression for f (x) as a product of irreducibles.
To see the uniqueness, suppose that
f (x) = p1 (x)p2 (x) .... pr (x) and
f (x) = q1 (x)q2 (x) : : : qs (x)
are two such expressions, with s > r. Then q1 (x)q2 (x)... qs (x) belongs to the ideal (p1 (x)) of F[x]. Since this ideal is prime (as p1(x) is irreducible) this means that either q1(x) ∈ (p1(x)) or q2(x)... qs(x) ∈ (p1(x)). Repeating this step leads to the conclusion that at least one of the qi (x) belongs to (p1(x)). After reordering the qi(x) if necessary we have q1(x) ∈ (p1(x)). Since q1 (x) is irreducible this means q1(x) = u1p1(x) for some unit u1. Then
Pl1(x)p2(x) ...pr(x) = u1p1(x)q2(x) ...qs(x).
Since F [x] is an integral domain we can cancel p1(x) from both sides to obtain
P2(x) .. .P1(x) = u1q2(x) . .. qs(x).
After repeating this step a further r - 1 times we have
1 = u1u2 . . . ur qr + 1(x) . .. qs(x),
where u1,... ,ur are units in F[x] (i.e. non-zero elements of F). This means s = r, since the polynomial on the right in the above expression must have degree zero. We conclude that qi (x),..., qs (x) are associates (in some order) of p1 (x),..., pr (x). This completes the proof.
|
161 videos|58 docs
|
FAQs on Unique Factorization Domain - Algebra - Mathematics
| 1. What is a Unique Factorization Domain (UFD) in mathematics? |  |
| 2. What are the main properties of a Unique Factorization Domain (UFD)? |  |
| 3. How does a Unique Factorization Domain (UFD) differ from a Euclidean Domain? |  |
| 4. What are some examples of Unique Factorization Domains (UFDs)? |  |
| 5. How is the concept of Unique Factorization Domain (UFD) important in number theory and algebraic geometry? |  |





















