Euclidean Domain | Algebra - Mathematics PDF Download
A Euclidean domain is an integral domain R which can be equipped with a function
d : R\{0} → N
such that for all a ∈ R and b ≠ 0, b ∈ R we can write
a = qb + r
for some q, r ∈ R with r = 0 or d(r) < d(b).
For example. Z with d(n) = |n| is a Euclidean Domain; also, for any field k, k[X ] with d(f ) = deg(f ) is a Euclidean Domain. (WARNING: In the second example above, it is essential that k be a field.)
We shall prove that every Euclidean Domain is a Principal Ideal Domain (and so also a Unique Factorization Domain). This shows that for any field k, k[X ] has unique factorization into irreducibles. As a further example, we prove that 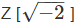 is a Euclidean Domain.
is a Euclidean Domain.
Proposition 1. In a Euclidean domain, every ideal is principal.
Proof. Suppose R is a Euclidean domain and 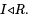 . Then EITHER I = {0} = (0) OR we can take a ≠ 0 in I with d(a) least; then for any b ∈ I , we can write b = qa + r with r = 0 or d(r) < d(a); but r = q − ba ∈ I and so by minimality of d(a), r = 0; thus a|b and I = (a).
. Then EITHER I = {0} = (0) OR we can take a ≠ 0 in I with d(a) least; then for any b ∈ I , we can write b = qa + r with r = 0 or d(r) < d(a); but r = q − ba ∈ I and so by minimality of d(a), r = 0; thus a|b and I = (a).
Corollary 2. If k is a field then every ideal in k[X ] is principal.
Corollary 3. Let k be a field. Then every polynomial in k[X ] can be factorized into primes=irreducibles, and the factorization is essential ly unique.
Corollary 4. Every element of the ring  can be factorized into primes= irreducibles, and the factorization is essential ly unique.
can be factorized into primes= irreducibles, and the factorization is essential ly unique.
Proof. By Theorem 1, it is enough to show that 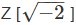 is a Euclidean Domain.To this end, define N :
is a Euclidean Domain.To this end, define N : 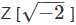 → N by
→ N by
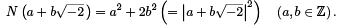
Note that we can extend N to a function N : Q  → Q defined similarly by
→ Q defined similarly by
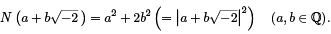
Note also that given any 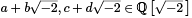 we have
we have
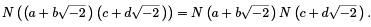
Now, suppose we are given 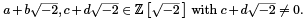
Then
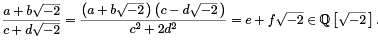
Pick 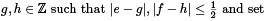
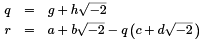
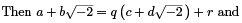
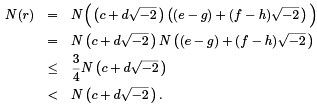
|
161 videos|58 docs
|
FAQs on Euclidean Domain - Algebra - Mathematics
| 1. What is an Euclidean domain in mathematics? |  |
| 2. How does the Euclidean algorithm relate to Euclidean domains? |  |
| 3. What are some examples of Euclidean domains? |  |
| 4. How can Euclidean domains be used in solving equations or factorizing numbers? |  |
| 5. Are all integral domains Euclidean domains? |  |


























