Mathematics Exam > Mathematics Notes > Calculus > Table of Laplace Transforms
Table of Laplace Transforms | Calculus - Mathematics PDF Download
Table of Laplace Transforms
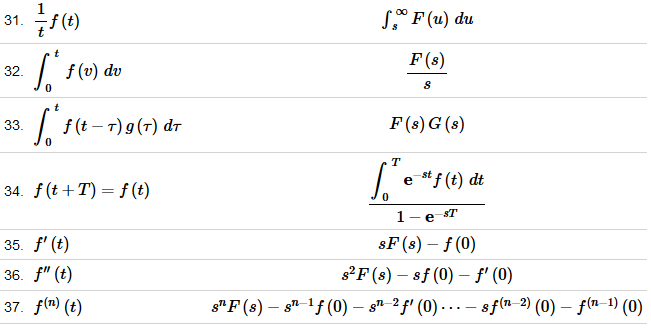
Table Notes
- This list is not a complete listing of Laplace transforms and only contains some of the more commonly used Laplace transforms and formulas.
- Recall the definition of hyperbolic functions.
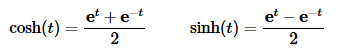
- Be careful when using “normal” trig function vs. hyperbolic functions. The only difference in the formulas is the “+a2” for the “normal” trig functions becomes a “−a2” for the hyperbolic functions!
- Formula #4 uses the Gamma function which is defined as
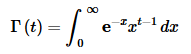
If n is a positive integer then,
Γ(n+1)=n!
The Gamma function is an extension of the normal factorial function. Here are a couple of quick facts for the Gamma function
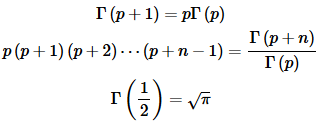
The document Table of Laplace Transforms | Calculus - Mathematics is a part of the Mathematics Course Calculus.
All you need of Mathematics at this link: Mathematics
|
112 videos|65 docs|3 tests
|
FAQs on Table of Laplace Transforms - Calculus - Mathematics
| 1. What is a Laplace transform? |  |
Ans. A Laplace transform is a mathematical operation that transforms a function of time, often a signal, into a function of a complex variable s, which represents frequency in the Laplace domain. It is commonly used in engineering and physics to solve differential equations and analyze linear systems.
| 2. How is the Laplace transform defined? | |
Ans. The Laplace transform of a function f(t), denoted by F(s), is defined as the integral of f(t) multiplied by e^(-st), where s is a complex number. The integral is taken from 0 to infinity. Mathematically, it can be represented as F(s) = ∫[0,∞] f(t) e^(-st) dt.
| 3. What are the advantages of using Laplace transforms? | |
Ans. There are several advantages of using Laplace transforms. Firstly, they can simplify the solution of differential equations by transforming them into algebraic equations. This makes it easier to solve complex problems. Secondly, Laplace transforms allow for the analysis of systems in the frequency domain, providing insights into system behavior at different frequencies. Finally, they have applications in control systems, circuit analysis, signal processing, and many other fields of engineering.
| 4. Can Laplace transforms be used to solve non-linear equations? | |
Ans. Laplace transforms are primarily used for linear systems and linear differential equations. However, they can sometimes be used to solve non-linear equations by linearizing them around a specific operating point. This involves approximating the non-linear function as a linear function in the vicinity of the operating point and then applying the Laplace transform. However, this approach may introduce errors and is not always applicable to all non-linear equations.
| 5. What is the inverse Laplace transform? | |
Ans. The inverse Laplace transform is the operation that converts a function F(s) in the Laplace domain back to its corresponding function f(t) in the time domain. It is denoted by L^(-1){F(s)}. The inverse Laplace transform is typically found using tables of Laplace transform pairs or by applying partial fraction decomposition and the residue theorem. It allows us to obtain the original function from its Laplace transform, enabling the solution of differential equations and the analysis of system responses in the time domain.
Related Exams
About this Document
|
4.85/5 Rating |
|
Dec 23, 2024 Last updated |
Document Description: Table of Laplace Transforms for Mathematics 2024 is part of Calculus preparation.
The notes and questions for Table of Laplace Transforms have been prepared according to the Mathematics exam syllabus. Information about Table of Laplace Transforms covers topics
like and Table of Laplace Transforms Example, for Mathematics 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Table of Laplace Transforms.
Introduction of Table of Laplace Transforms in English is available as part of our Calculus
for Mathematics & Table of Laplace Transforms in Hindi for Calculus course.
Download more important topics related with notes, lectures and mock test series for Mathematics
Exam by signing up for free. Mathematics: Table of Laplace Transforms | Calculus - Mathematics
Description
Full syllabus notes, lecture & questions for Table of Laplace Transforms | Calculus - Mathematics - Mathematics | Plus excerises question with solution to help you revise complete syllabus for Calculus | Best notes, free PDF download
Information about Table of Laplace Transforms
In this doc you can find the meaning of Table of Laplace Transforms defined & explained in the simplest way possible. Besides explaining types of
Table of Laplace Transforms theory, EduRev gives you an ample number of questions to practice Table of Laplace Transforms tests, examples and also practice Mathematics
tests
|
Explore Courses for Mathematics exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Viva Questions
,video lectures
,Table of Laplace Transforms | Calculus - Mathematics
,Important questions
,practice quizzes
,study material
,MCQs
,Objective type Questions
,shortcuts and tricks
,Previous Year Questions with Solutions
,Free
,Semester Notes
,Table of Laplace Transforms | Calculus - Mathematics
,Exam
,mock tests for examination
,Sample Paper
,past year papers
,Table of Laplace Transforms | Calculus - Mathematics
,Summary
,ppt
,Extra Questions
;
Additional Information about Table of Laplace Transforms for Mathematics Preparation
Table of Laplace Transforms Free PDF Download
The Table of Laplace Transforms is an invaluable resource that delves deep into the core of the Mathematics exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Table of Laplace Transforms now and kickstart your journey towards success in the Mathematics exam.
Importance of Table of Laplace Transforms
The importance of Table of Laplace Transforms cannot be overstated, especially for Mathematics aspirants.
This document holds the key to success in the Mathematics exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Table of Laplace Transforms Notes
Table of Laplace Transforms Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Table of Laplace Transforms.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Table of Laplace Transforms Notes on EduRev are your ultimate resource for success.
Table of Laplace Transforms Mathematics Questions
The "Table of Laplace Transforms Mathematics Questions" guide is a valuable resource for all aspiring students preparing for the
Mathematics exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Table of Laplace Transforms on the App
Students of Mathematics can study Table of Laplace Transforms alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Table of Laplace Transforms,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Table of Laplace Transforms is prepared as per the latest Mathematics syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup