Chain Rule | Calculus - Mathematics PDF Download
We’ve taken a lot of derivatives over the course of the last few sections. However, if you look back they have all been functions similar to the following kinds of functions.
R(z)=√z f(t)=t50 y=tan(x) h(w)=ew g(x)=lnx
These are all fairly simple functions in that wherever the variable appears it is by itself. What about functions like the following,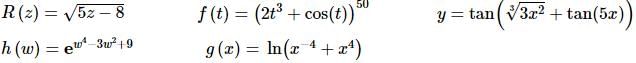
None of our rules will work on these functions and yet some of these functions are closer to the derivatives that we’re liable to run into than the functions in the first set.
Let’s take the first one for example. Back in the section on the definition of the derivative we actually used the definition to compute this derivative. In that section we found that,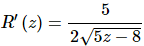
If we were to just use the power rule on this we would get,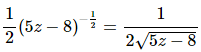
which is not the derivative that we computed using the definition. It is close, but it’s not the same. So, the power rule alone simply won’t work to get the derivative here.
Let’s keep looking at this function and note that if we define,
f(z)=√z g(z)=5z−8
then we can write the function as a composition.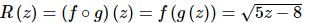
and it turns out that it’s actually fairly simple to differentiate a function composition using the Chain Rule. There are two forms of the chain rule. Here they are.
Chain Rule
Suppose that we have two functions f(x) and g(x) and they are both differentiable.
1. If we define F(x) = (f∘g) (x) then the derivative of F(x) is,
F′(x) = f′(g(x)) g′(x)
2. If we have y = f(u) and u = g(x) then the derivative of y is
Each of these forms have their uses, however we will work mostly with the first form in this class. To see the proof of the Chain Rule see the Proof of Various Derivative Formulas section of the Extras chapter.
Now, let’s go back and use the Chain Rule on the function that we used when we opened this section.
Example 1 Use the Chain Rule to differentiate 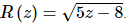
We’ve already identified the two functions that we needed for the composition, but let’s write them back down anyway and take their derivatives.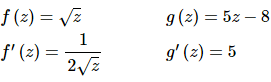
So, using the chain rule we get,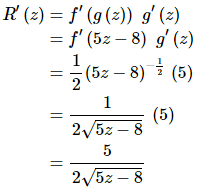
And this is what we got using the definition of the derivative.
In general, we don’t really do all the composition stuff in using the Chain Rule. That can get a little complicated and in fact obscures the fact that there is a quick and easy way of remembering the chain rule that doesn’t require us to think in terms of function composition.
Let’s take the function from the previous example and rewrite it slightly.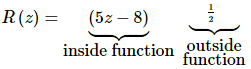
This function has an “inside function” and an “outside function”. The outside function is the square root or the exponent of 1/2 depending on how you want to think of it and the inside function is the stuff that we’re taking the square root of or raising to the 1/2, again depending on how you want to look at it.
The derivative is then,
In general, this is how we think of the chain rule. We identify the “inside function” and the “outside function”. We then differentiate the outside function leaving the inside function alone and multiply all of this by the derivative of the inside function. In its general form this is,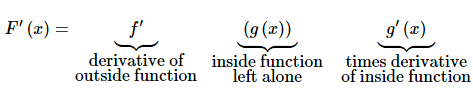
We can always identify the “outside function” in the examples below by asking ourselves how we would evaluate the function. For instance in the R(z) case if we were to ask ourselves what R(2) is we would first evaluate the stuff under the radical and then finally take the square root of this result. The square root is the last operation that we perform in the evaluation and this is also the outside function. The outside function will always be the last operation you would perform if you were going to evaluate the function.
Let’s take a look at some examples of the Chain Rule.
Example 2 Differentiate each of the following.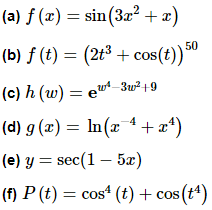
Solution:
(a) f(x) = sin(3x2 + x)
It looks like the outside function is the sine and the inside function is 3x2+x. The derivative is then.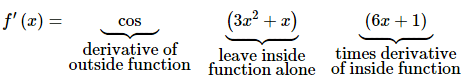
Or with a little rewriting,
f′(x) = (6 + 1) cos(3x2 + x)
(b) f (t) = (2t3 + cos(t))50
In this case the outside function is the exponent of 50 and the inside function is all the stuff on the inside of the parenthesis. The derivative is then.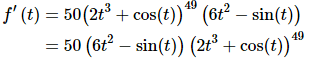
(c) h (w) = ew4-3w2+9
Identifying the outside function in the previous two was fairly simple since it really was the “outside” function in some sense. In this case we need to be a little careful. Recall that the outside function is the last operation that we would perform in an evaluation. In this case if we were to evaluate this function the last operation would be the exponential. Therefore, the outside function is the exponential function and the inside function is its exponent.
Here’s the derivative.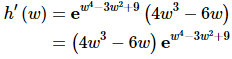
Remember, we leave the inside function alone when we differentiate the outside function. So, the derivative of the exponential function (with the inside left alone) is just the original function.
(d) g(x)=ln(x−4 + x4)
Here the outside function is the natural logarithm and the inside function is stuff on the inside of the logarithm.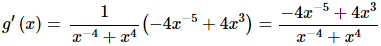
Again remember to leave the inside function alone when differentiating the outside function. So, upon differentiating the logarithm we end up not with 1/x but instead with 1/(inside function).
(e) y=sec(1−5x)
In this case the outside function is the secant and the inside is the 1−5x.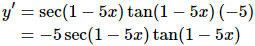
In this case the derivative of the outside function is sec(x)tan(x). However, since we leave the inside function alone we don’t get x’s in both. Instead we get 1−5x in both.
(f) P(t)=cos4(t)+cos(t4)
There are two points to this problem. First, there are two terms and each will require a different application of the chain rule. That will often be the case so don’t expect just a single chain rule when doing these problems. Second, we need to be very careful in choosing the outside and inside function for each term.
Recall that the first term can actually be written as,
cos4(t)=(cos(t))4
So, in the first term the outside function is the exponent of 4 and the inside function is the cosine. In the second term it’s exactly the opposite. In the second term the outside function is the cosine and the inside function is t4. Here’s the derivative for this function.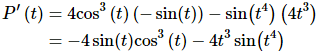
There are a couple of general formulas that we can get for some special cases of the chain rule. Let’s take a quick look at those.
Example 3 Differentiate each of the following.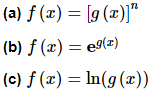
(a) The outside function is the exponent and the inside is g(x).
f′(x) = n[g(x)]n−1 g′(x)
(b) The outside function is the exponential function and the inside is g(x).
f′(x)=g′(x) eg(x)
(c) The outside function is the logarithm and the inside is g(x).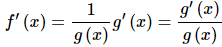
The formulas in this example are really just special cases of the Chain Rule but may be useful to remember in order to quickly do some of these derivatives.
Now, let’s also not forget the other rules that we’ve got for doing derivatives. For the most part we’ll not be explicitly identifying the inside and outside functions for the remainder of the problems in this section. We will be assuming that you can see our choices based on the previous examples and the work that we have shown.
Example 4 Differentiate each of the following.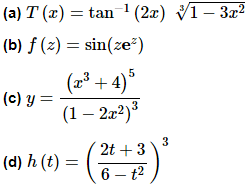
Solution:
Let’s first notice that this problem is first and foremost a product rule problem. This is a product of two functions, the inverse tangent and the root and so the first thing we’ll need to do in taking the derivative is use the product rule. However, in using the product rule and each derivative will require a chain rule application as well.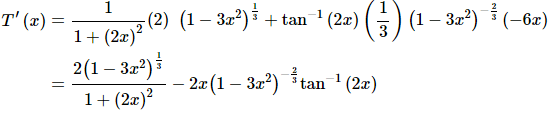
In this part be careful with the inverse tangent. We know that,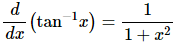
When doing the chain rule with this we remember that we’ve got to leave the inside function alone. That means that where we have the x2 in the derivative of tan−1 x we will need to have (inside function)2 .
(b) f(z) = sin(zez)
Now contrast this with the previous problem. In the previous problem we had a product that required us to use the chain rule in applying the product rule. In this problem we will first need to apply the chain rule and when we go to integrate the inside function we’ll need to use the product rule.
Here is the chain rule portion of the problem.
In this case we did not actually do the derivative of the inside yet. We just left it in the derivative notation to make it clear that in order to do the derivative of the inside function we now have a product rule.
Here is the rest of the work for this problem.
f′(z)=cos(zez)(ez+zez)
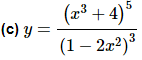
For this problem we clearly have a rational expression and so the first thing that we’ll need to do is apply the quotient rule. In the process of using the quotient rule we’ll need to use the chain rule when differentiating the numerator and denominator. 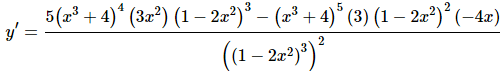
These tend to be a little messy. Notice that when we go to simplify that we’ll be able to a fair amount of factoring in the numerator and this will often greatly simplify the derivative.
After factoring we were able to cancel some of the terms in the numerator against the denominator. So even though the initial chain rule was fairly messy the final answer is significantly simpler because of the factoring.
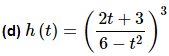
Unlike the previous problem the first step for derivative is to use the chain rule and then once we go to differentiate the inside function we’ll need to do the quotient rule.
Here is the work for this problem.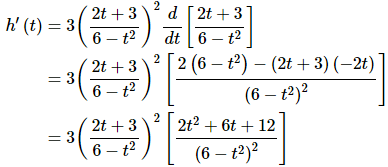
As with the second part above we did not initially differentiate the inside function in the first step to make it clear that it would be quotient rule from that point on.
There were several points in the last example. First is to not forget that we’ve still got other derivatives rules that are still needed on occasion. Just because we now have the chain rule does not mean that the product and quotient rule will no longer be needed.
In addition, as the last example illustrated, the order in which they are done will vary as well. Some problems will be product or quotient rule problems that involve the chain rule. Other problems however, will first require the use the chain rule and in the process of doing that we’ll need to use the product and/or quotient rule.
Most of the examples in this section won’t involve the product or quotient rule to make the problems a little shorter. However, in practice they will often be in the same problem so you need to be prepared for these kinds of problems.
Now, let’s take a look at some more complicated examples.
Example 5 Differentiate each of the following.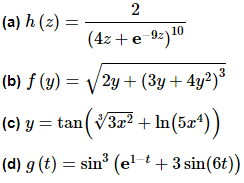
Solution: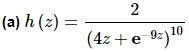
In this case let’s first rewrite the function in a form that will be a little easier to deal with.
h(z)=2(4z+e−9z)−10
Now, let’s start the derivative.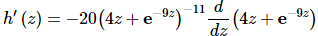
Notice that we didn’t actually do the derivative of the inside function yet. This is to allow us to notice that when we do differentiate the second term we will require the chain rule again. Notice as well that we will only need the chain rule on the exponential and not the first term. In many functions we will be using the chain rule more than once so don’t get excited about this when it happens.
Let’s go ahead and finish this example out.
h′(z)=−20(4z+e−9z)−11(4−9e−9z)
Be careful with the second application of the chain rule. Only the exponential gets multiplied by the “-9” since that’s the derivative of the inside function for that term only. One of the more common mistakes in these kinds of problems is to multiply the whole thing by the “-9” and not just the second term.
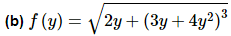
We’ll not put as many words into this example, but we’re still going to be careful with this derivative so make sure you can follow each of the steps here.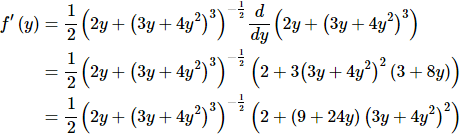
As with the first example the second term of the inside function required the chain rule to differentiate it. Also note that again we need to be careful when multiplying by the derivative of the inside function when doing the chain rule on the second term.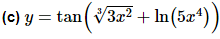
Let’s jump right into this one.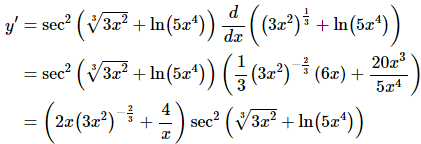
In this example both of the terms in the inside function required a separate application of the chain rule.
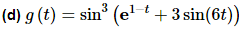
We’ll need to be a little careful with this one.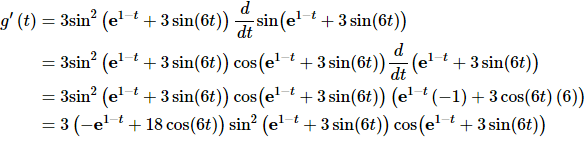
This problem required a total of 4 chain rules to complete.
Sometimes these can get quite unpleasant and require many applications of the chain rule. Initially, in these cases it’s usually best to be careful as we did in this previous set of examples and write out a couple of extra steps rather than trying to do it all in one step in your head. Once you get better at the chain rule you’ll find that you can do these fairly quickly in your head.
Finally, before we move onto the next section there is one more issue that we need to address. In the Derivatives of Exponential and Logarithm Functions section we claimed that,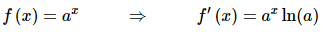
but at the time we didn’t have the knowledge to do this. We now do. What we needed was the chain rule.
First, notice that using a property of logarithms we can write a as,
a=elna
This may seem kind of silly, but it is needed to compute the derivative. Now, using this we can write the function as,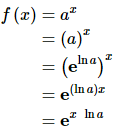
Okay, now that we’ve gotten that taken care of all we need to remember is that a is a constant and so lna is also a constant. Now, differentiating the final version of this function is a (hopefully) fairly simple Chain Rule problem.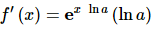
Now, all we need to do is rewrite the first term back as ax to get,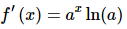
So, not too bad if you can see the trick to rewriting the a and with using the Chain Rule.
Practice problems: Chain Rule
For problems 1 – 27 differentiate the given function.
1. Differentiate f(x) = (6x2 + 7x)4.
Solution:
For this problem the outside function is (hopefully) clearly the exponent of 4 on the parenthesis while the inside function is the polynomial that is being raised to the power. The derivative is then,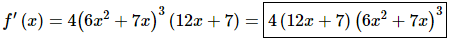
2. Differentiate g(t) = (4t2 − 3t + 2)−2.
Solution:
For this problem the outside function is (hopefully) clearly the exponent of -2 on the parenthesis while the inside function is the polynomial that is being raised to the power. The derivative is then,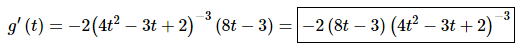
3. Differentiate 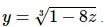
Solution:
For this problem, after converting the root to a fractional exponent, the outside function is (hopefully) clearly the exponent of 1/3 while the inside function is the polynomial that is being raised to the power (or the polynomial inside the root – depending upon how you want to think about it). The derivative is then,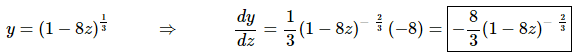
4. Differentiate R(w) = csc(7w).
Solution:
For this problem the outside function is (hopefully) clearly the trig function and the inside function is the stuff inside of the trig function. The derivative is then,
In dealing with functions like cosecant (or secant for that matter) be careful to make sure that the inside function gets substituted into both terms of the derivative of the outside function. One of the more common mistakes with this kind of problem is to only substitute the 7w into only the cosecant or only the cotangent instead of both as it should be.
5. Differentiate G(x) = 2sin(3x + tan( x )).
Solution:
For this problem the outside function is (hopefully) clearly the sine function and the inside function is the stuff inside of the trig function. The derivative is then,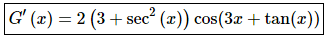
6. Differentiate h(u) = tan(4 + 10u).
Solution:
For this problem the outside function is (hopefully) clearly the trig function and the inside function is the stuff inside of the trig function. The derivative is then,
7. Differentiate f(t) = 5 + e4t + t7.
Solution:
Note that we only need to use the Chain Rule on the second term as we can differentiate the first term without the Chain Rule.
Now, recall that for exponential functions outside function is the exponential function itself and the inside function is the exponent. The derivative is then,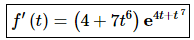
8. Differentiate g(x) = e1 − cos(x).
Solution:
For exponential functions remember that the outside function is the exponential function itself and the inside function is the exponent. The derivative is then,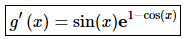
9. Differentiate H(z) = 21 − 6z.
Solution:
For exponential functions remember that the outside function is the exponential function itself and the inside function is the exponent. The derivative is then,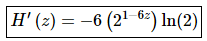
10. Differentiate u(t) = tan−1(3t − 1).
Solution:
For this problem the outside function is (hopefully) clearly the inverse tangent and the inside function is the stuff inside of the inverse tangent. The derivative is then,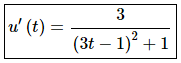
11. Differentiate F(y) = ln(1 − 5y2 + y3).
Solution:
For this problem the outside function is (hopefully) clearly the logarithm and the inside function is the stuff inside of the logarithm. The derivative is then,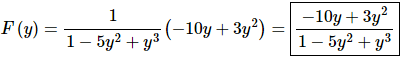
With logarithm problems remember that after differentiating the logarithm (i.e. the outside function) you need to substitute the inside function into the derivative. So, instead of getting just,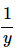
we get the following (i.e. we plugged the inside function into the derivative),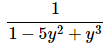
Then, we can’t forget of course to multiply by the derivative of the inside function.
12. Differentiate V(x) = ln(sin(x) − cot(x)).
Solution:
For this problem the outside function is (hopefully) clearly the logarithm and the inside function is the stuff inside of the logarithm. The derivative is then,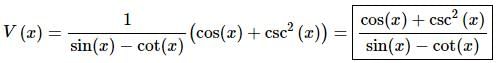
With logarithm problems remember that after differentiating the logarithm (i.e. the outside function) you need to substitute the inside function into the derivative. So, instead of getting just,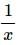
we get the following (i.e. we plugged the inside function into the derivative),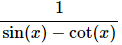
Then, we can’t forget of course to multiply by the derivative of the inside function.
13. Differentiate h(z) = sin(z6) + sin6(z).
Solution:
For this problem each term will require a separate application of the Chain Rule and don’t forget that,
sin6(z)=[sin(z)]6
So, in the first term the outside function is the sine function, while the sine function is the inside function in the second term. The derivative is then,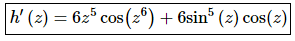
14. Differentiate 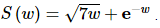
Solution:
For this problem each term will require a separate application of the Chain Rule and make sure you are careful with parenthesis in dealing with the root in the first term.
The derivative is then,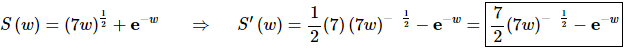
15. Differentiate g(z) = 3z7 − sin(z2 + 6).
Solution:
For this problem the first term requires no Chain Rule and the second term will require the Chain Rule. The derivative is then,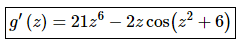
16. Differentiate f ( x ) = ln ( sin ( x ) ) − ( x 4 − 3 x ) 10 .
Solution:
For this problem each term will require a separate application of the Chain Rule. The derivative is then,
17. Differentiate 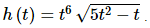
Solution:
For this problem we’ll need to do the Product Rule to start off the derivative. In the process we’ll need to use the Chain Rule when we differentiate the second term.
The derivative is then,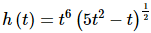
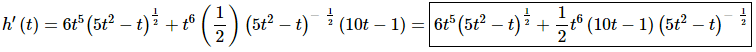
18. Differentiate q(t) = t2ln(t5).
Solution:
For this problem we’ll need to do the Product Rule to start off the derivative. In the process we’ll need to use the Chain Rule when we differentiate the second term.
The derivative is then,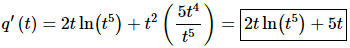
19. Differentiate g(w) = cos(3w) sec(1 − w).
Solution:
For this problem we’ll need to do the Product Rule to start off the derivative. In the process we’ll need to use the Chain Rule when we differentiate each term.
The derivative is then,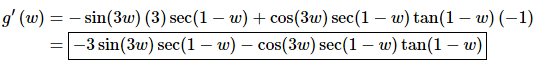
20. Differentiate 
Solution:
For this problem we’ll need to do the Quotient Rule to start off the derivative. In the process we’ll need to use the Chain Rule when we differentiate the numerator.
The derivative is then,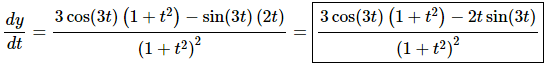
21. Differentiate 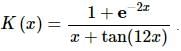
Solution:
For this problem we’ll need to do the Quotient Rule to start off the derivative. In the process we’ll need to use the Chain Rule when we differentiate both the numerator and the denominator.
The derivative is then,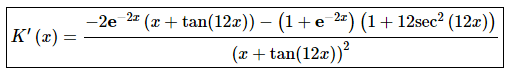
22. Differentiate f(x) = cos(x2ex).
Solution:
For this problem we’ll start off using the Chain Rule, however when we differentiate the inside function we’ll need to do the Product Rule.
The derivative is then,
f′(x)=−(2xex+x2ex)sin(x2ex)
23. Differentiate 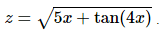
Solution:
Step 1
This problem will require multiple uses of the Chain Rule and so we’ll step though the derivative process to make each use clear.
Here is the first step of the derivative and we’ll need to use the Chain Rule in this step.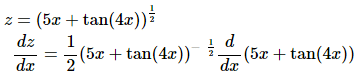
Step 2
In this step we can see that we’ll need to use the Chain Rule on the second term.
The derivative is then,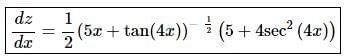
In this step we were using the Chain Rule on the second term and so when multiplying by the derivative of the inside function we only multiply the second term by the derivative of the inside function and not both terms.
24. Differentiate f(t) = (e−6t + sin(2 − t))3.
Solution:
Step 1
This problem will require multiple uses of the Chain Rule and so we’ll step though the derivative process to make each use clear.
Here is the first step of the derivative and we’ll need to use the Chain Rule in this step.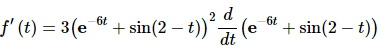
Step 2
In this step we can see that we’ll need to use the Chain Rule on each of the terms.
The derivative is then,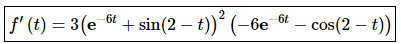
25. Differentiate g(x) = (ln(x2 + 1) − tan−1 (6x))10.
Solution:
Step 1
This problem will require multiple uses of the Chain Rule and so we’ll step though the derivative process to make each use clear.
Here is the first step of the derivative and we’ll need to use the Chain Rule in this step.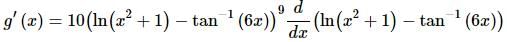 Step 2
Step 2
In this step we can see that we’ll need to use the Chain Rule on each of the terms.
The derivative is then,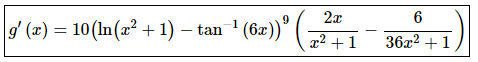
26. Differentiate h(z) = tan4(z2 + 1).
solution:
Step 1
This problem will require multiple uses of the Chain Rule and so we’ll step though the derivative process to make each use clear. Also, recall that,
tan4(x)=[tan(x)]4
Here is the first step of the derivative and we’ll need to use the Chain Rule in this step.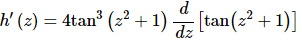
Step 2
As we can see the derivative from the previous step will also require the Chain Rule.
The derivative is then,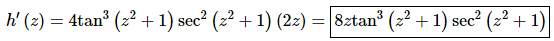
27. Differentiate 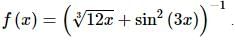
Solution:
Step 1
This problem will require multiple uses of the Chain Rule and so we’ll step though the derivative process to make each use clear.
Here is the first step of the derivative and we’ll need to use the Chain Rule in this step.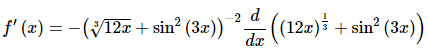
Step 2
As we can see the derivative from the previous step will also require the Chain Rule on each of the terms.
The derivative from this step is,
Step 3
The second term will again use the Chain Rule as we can see.
The derivative is then,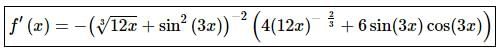
28. Find the tangent line to f(x) = 4√2x − 6e2− x atx = 2.
Solution:
Step 1
We know that the derivative of the function will give us the slope of the tangent line so we’ll need the derivative of the function. Differentiating each term will require the Chain Rule as well.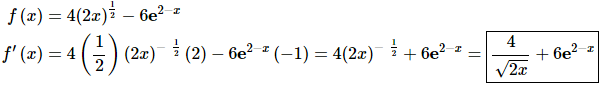
Step 2
Now all we need to do is evaluate the function and the derivative at the point in question.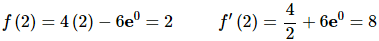
Step 3
Now all that we need to do is write down the equation of the tangent line.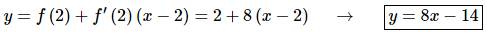
29. Determine where V(z) = z4(2z − 8)3 is increasing and decreasing.
Solution:
step 1
We’ll first need the derivative because we know that the derivative will give us the rate of change of the function. Here is the derivative.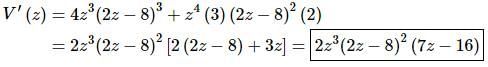
Note that we factored the derivative to help with the next step. In general, we don’t need to do this.
Step 2
Next, we need to know where the function is not changing and so all we need to do is set the derivative equal to zero and solve. In this case it’s pretty easy to spot where the derivative will be zero.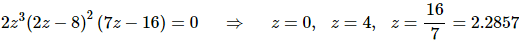
Step 3
To get the answer to this problem all we need to know is where the derivative is positive (and hence the function is increasing) or negative (and hence the function is decreasing). Because the derivative is continuous we know that the only place it can change sign is where the derivative is zero. So, as we did in this section a quick number line will give us the sign of the derivative for the various intervals.
Here is the number line for this problem.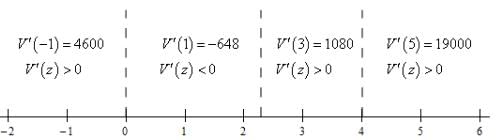
From this we get the following increasing/decreasing information.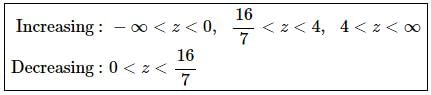
30. The position of an object is given by s(t) = sin(3t) − 2t + 4 . Determine where in the interval [0,3] the object is moving to the right and moving to the left.
Solution:
Step 1
We’ll first need the derivative because we know that the derivative will give us the velocity of the object. Here is the derivative.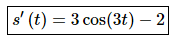
Step 2
Next, we need to know where the object stops moving and so all we need to do is set the derivative equal to zero and solve.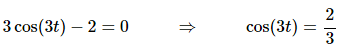
A quick calculator computation tells us that,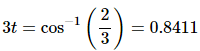
Recalling our work in the Review chapter and a quick check on a unit circle we can see that either 3t=−0.8411 or 3t=2π−0.8411=5.4421 can be used for the second angle. Note that either will work, but we’ll use the second simply because it is the positive angle.
Putting all of this together and dividing by 3 we can see that the derivative will be zero at,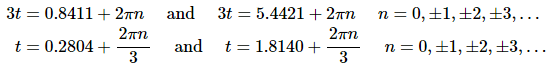
Finally, all we need to so is plug in some n’s to determine which solutions fall in the interval we are working on, [0,6].
So, in the interval [0,6], the object stops moving at the following three points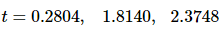
Step 3
To get the answer to this problem all we need to know is where the derivative is positive (and hence the object is moving to the right) or negative (and hence the object is moving to the left). Because the derivative is continuous we know that the only place it can change sign is where the derivative is zero. So, as we did in this section a quick number line will give us the sign of the derivative for the various intervals.
Here is the number line for this problem.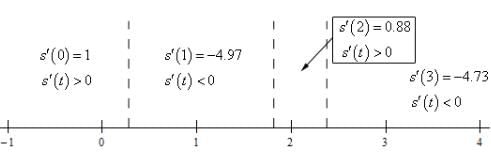
From this we get the following moving right/moving left information.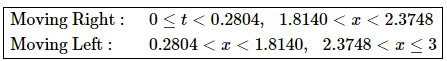
Note that because we’ve only looked at what is happening in the interval [0,3] we can’t say anything about the moving right/moving left behavior of the object outside of this interval.
31. Determine where A(t) = t2e5−t is increasing and decreasing.
Solution:
Step 1
We’ll first need the derivative because we know that the derivative will give us the rate of change of the function. Here is the derivative.
Note that we factored the derivative to help with the next step. In general, we don’t need to do this.
Step 2
Next, we need to know where the function is not changing and so all we need to do is set the derivative equal to zero and solve. In this case it’s pretty easy to spot where the derivative will be zero.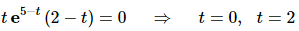
Step 3
To get the answer to this problem all we need to know is where the derivative is positive (and hence the function is increasing) or negative (and hence the function is decreasing). Because the derivative is continuous we know that the only place it can change sign is where the derivative is zero. So, as we did in this section a quick number line will give us the sign of the derivative for the various intervals.
Here is the number line for this problem.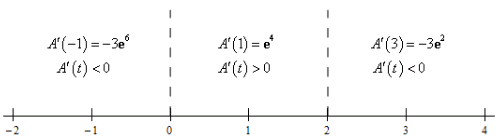
From this we get the following increasing/decreasing information.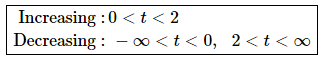
32. Determine where in the interval [−1, 20] the function f(x) = ln(x4 + 20x3 + 100) is increasing and decreasing.
Solution:
Step 1
We’ll first need the derivative because we know that the derivative will give us the rate of change of the function. Here is the derivative.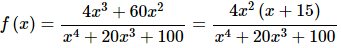
Note that we factored the numerator to help with the next step. In general, we don’t need to do this.
Step 2
Next, we need to know where the function is not changing and so all we need to do is set the derivative equal to zero and solve.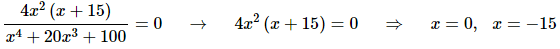
Note, that in general, we also need to be concerned with where the derivative is not defined as well. Functions can (and often do) change sign where they are not defined. In this case however we’ve restricted the interval down to a range where the function exists and is continuous on the given interval and so this is something we need to worry about for this problem.
In the next Chapter we will start also looking at what happens if the derivative is also not defined at particular points.
Note as well that we really should at this point step back and recall that we are working on the interval [−1, 20]. We are only interested in what is happening on this interval and so we should make sure that the points found above are inside the interval.
In this case only x = 0 is in the interval and so we’ll need to exclude x = −15 from our work for the rest of this problem.
Step 3
To get the answer to this problem all we need to know is where the derivative is positive (and hence the function is increasing) or negative (and hence the function is decreasing). Because the derivative is continuous we know that the only place it can change sign is where the derivative is zero. So, as we did in this section a quick number line will give us the sign of the derivative for the various intervals.
Here is the number line for this problem.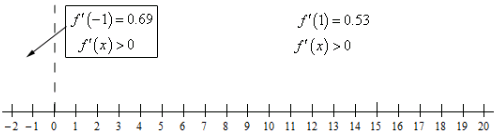
So, we can see that, in this case function is increasing everywhere in the interval [−1,20] except x=0. Recall that at this point the derivative was zero and hence the function is not changing (and therefore can’t be increasing).
So, the formal answer for this problem is,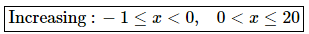
Note that because we’ve only looked at what is happening in the interval [−1,20] we can’t say anything about the increasing/decreasing nature of the function outside of this interval.
|
112 videos|65 docs|3 tests
|
FAQs on Chain Rule - Calculus - Mathematics
| 1. What is the chain rule in mathematics? |  |
| 2. How do you apply the chain rule to find derivatives? |  |
| 3. Can you provide an example of applying the chain rule? |  |
| 4. Why is the chain rule important in calculus? |  |
| 5. Can the chain rule be applied to higher dimensions and multiple variables? |  |
















