Intervals of Validity | Calculus - Mathematics PDF Download
We’ve called this section Intervals of Validity because all of the examples will involve them. However, there is a lot more to this section. We will see a couple of theorems that will tell us when we can solve a differential equation. We will also see some of the differences between linear and nonlinear differential equations.
First let's take a look at a theorem about linear first order differential equations. This is a very important theorem although we’re not going to really use it for its most important aspect.
Theorem 1
Consider the following IVP.
y′+p(t)y=g(t)y(t0)=y0
If p ( t ) and g ( t ) are continuous functions on an open interval α < t < β and the interval contains t o , then there is a unique solution to the IVP on that interval.
So, just what does this theorem tell us? First, it tells us that for nice enough linear first order differential equations solutions are guaranteed to exist and more importantly the solution will be unique. We may not be able to find the solution but do know that it exists and that there will only be one of them. This is the very important aspect of this theorem. Knowing that a differential equation has a unique solution is sometimes more important than actually having the solution itself!
Next, if the interval in the theorem is the largest possible interval on which p (t) and g (t) are continuous then the interval is the interval of validity for the solution. This means, that for linear first order differential equations, we won't need to actually solve the differential equation in order to find the interval of validity. Notice as well that the interval of validity will depend only partially on the initial condition. The interval must contain to , but the value of yo , has no effect on the interval of validity.
Let’s take a look at an example.
Example 1: Without solving, determine the interval of validity for the following initial value problem.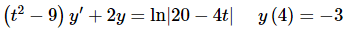
Solution: First, in order to use the theorem to find the interval of validity we must write the differential equation in the proper form given in the theorem. So we will need to divide out by the coefficient of the derivative.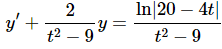
Next, we need to identify where the two functions are not continuous. This will allow us to find all possible intervals of validity for the differential equation. So, p ( t ) will be discontinuous at t = ± 3 since these points will give a division by zero. Likewise, g ( t ) will also be discontinuous at t = ± 3 as well as t = 5 since at this point we will have the natural logarithm of zero. Note that in this case we won't have to worry about natural log of negative numbers because of the absolute values.
Now, with these points in hand we can break up the real number line into four intervals where both p (t) and g (t) will be continuous. These four intervals are,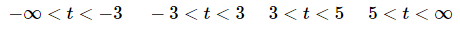
The endpoints of each of the intervals are points where at least one of the two functions is discontinuous. This will guarantee that both functions are continuous everywhere in each interval.
Finally, let's identify the actual interval of validity for the initial value problem. The actual interval of validity is the interval that will contain to = 4 . So, the interval of validity for the initial value problem is.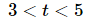
In this last example we need to be careful to not jump to the conclusion that the other three intervals cannot be intervals of validity. By changing the initial condition, in particular the value of to , we can make any of the four intervals the interval of validity.
The first theorem required a linear differential equation. There is a similar theorem for non-linear first order differential equations. This theorem is not as useful for finding intervals of validity as the first theorem was so we won’t be doing all that much with it.
Here is the theorem.
Theorem 2
Consider the following IVP.
y′=f(t,y) y(t0)=y0
If f ( t , y ) and ∂f/∂y are continuous functions in some rectangle α < t < β , γ < y < δ containing the point ( t o y o ) then there is a unique solution to the IVP in some interval to – h < t < to + h that is contained in α < t < β.
Example 2: Determine all possible solutions to the following IVP.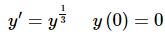
Solution: First, notice that this differential equation does NOT satisfy the conditions of the theorem.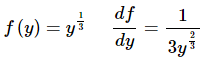
So, the function is continuous on any interval, but the derivative is not continuous at y = 0 and so will not be continuous at any interval containing y = 0 . In order to use the theorem both must be continuous on an interval that contains yo = 0 and this is problem for us since we do have yo = 0.
Now, let’s actually work the problem. This differential equation is separable and is fairly simple to solve.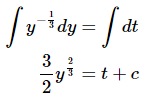
Applying the initial condition gives c = 0 and so the solution is.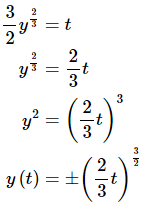
So, we’ve got two possible solutions here, both of which satisfy the differential equation and the initial condition. There is also a third solution to the IVP. y(t) = 0 is also a solution to the differential equation and satisfies the initial condition.
In this last example we had a very simple IVP and it only violated one of the conditions of the theorem, yet it had three different solutions. All the examples we’ve worked in the previous sections satisfied the conditions of this theorem and had a single unique solution to the IVP. This example is a useful reminder of the fact that, in the field of differential equations, things don’t always behave nicely. It’s easy to forget this as most of the problems that are worked in a differential equations class are nice and behave in a nice, predictable manner.
Let’s work one final example that will illustrate one of the differences between linear and non-linear differential equations.
Before proceeding in this problem, we should note that the differential equation is non-linear and meets both conditions of the Theorem 2 and so there will be a unique solution to the IVP for each possible value of yo . Also, note that the problem asks for any dependence of the interval of validity on the value of yo . This immediately illustrates a difference between linear and non-linear differential equations. Intervals of validity for linear differential equations do not depend on the value of yo . Intervals of validity for non-linear differential can depend on the value of y o as we pointed out after the second theorem. So, let’s solve the IVP and get some intervals of validity. First note that if yo = 0 then y (t) = 0 is the solution and this has an interval of validity of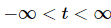
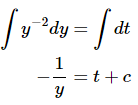
Applying the initial condition gives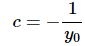
The solution is then.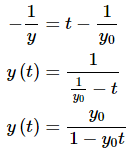
Now that we have a solution to the initial value problem we can start finding intervals of validity. From the solution we can see that the only problem that we’ll have is division by zero at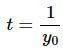
This leads to two possible intervals of validity.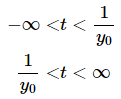
That actual interval of validity will be the interval that contains to = 0 . This however, depends on the value of yo . If yo 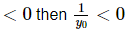 and so the second interval will contain to = 0. Likewise,
and so the second interval will contain to = 0. Likewise,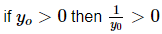 and in this case the first interval will contain to=0.
and in this case the first interval will contain to=0.
This leads to the following possible intervals of validity, depending on the value of yo.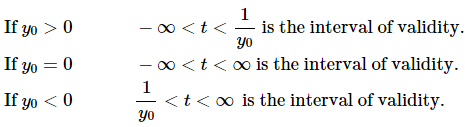
On a side note, notice that the solution, in its final form, will also work if yo=0.
So, what did this example show us about the difference between linear and non-linear differential equations?
First, as pointed out in the solution to the example, intervals of validity for non-linear differential equations can depend on the value of y o , whereas intervals of validity for linear differential equations don’t.
Second, intervals of validity for linear differential equations can be found from the differential equation with no knowledge of the solution. This is definitely not the case with non-linear differential equations. It would be very difficult to see how any of these intervals in the last example could be found from the differential equation. Knowledge of the solution was required in order for us to find the interval of validity.
Equilibrium Solutions
In the previous section we modeled a population based on the assumption that the growth rate would be a constant. However, in reality this doesn’t make much sense. Clearly a population cannot be allowed to grow forever at the same rate. The growth rate of a population needs to depend on the population itself. Once a population reaches a certain point the growth rate will start reduce, often drastically. A much more realistic model of a population growth is given by the logistic growth equation. Here is the logistic growth equation.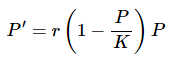
In the logistic growth equation r is the intrinsic growth rate and is the same r as in the last section. In other words, it is the growth rate that will occur in the absence of any limiting factors. K is called either the saturation level or the carrying capacity.
Now, we claimed that this was a more realistic model for a population. Let’s see if that in fact is correct. To allow us to sketch a direction field let’s pick a couple of numbers for r and K . We’ll use 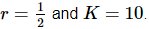 For these values the logistics equation is.
For these values the logistics equation is.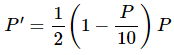
If you need a refresher on sketching direction fields go back and take a look at that section. First notice that the derivative will be zero at P = 0 and P = 10 . Also notice that these are in fact solutions to the differential equation. These two values are called equilibrium solutions since they are constant solutions to the differential equation. We’ll leave the rest of the details on sketching the direction field to you. Here is the direction field as well as a couple of solutions sketched in as well.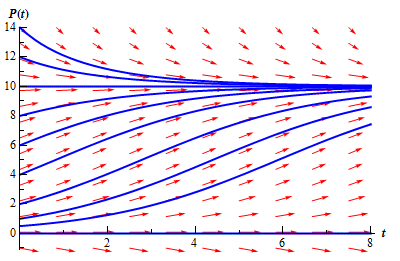
Note, that we included a small portion of negative P ’s in here even though they really don’t make any sense for a population problem. The reason for this will be apparent down the road. Also, notice that a population of say 8 doesn’t make all that much sense so let’s assume that population is in thousands or millions so that 8 actually represents 8,000 or 8,000,000 individuals in a population.
Notice that if we start with a population of zero, there is no growth and the population stays at zero. So, the logistic equation will correctly figure out that. Next, notice that if we start with a population in the range 0 < P ( 0 ) < 10 then the population will grow, but start to level off once we get close to a population of 10. If we start with a population of 10, the population will stay at 10. Finally, if we start with a population that is greater than 10, then the population will actually die off until we start nearing a population of 10, at which point the population decline will start to slow down.
Now, from a realistic standpoint this should make some sense. Populations can’t just grow forever without bound. Eventually the population will reach such a size that the resources of an area are no longer able to sustain the population and the population growth will start to slow as it comes closer to this threshold. Also, if you start off with a population greater than what an area can sustain there will actually be a die off until we get near to this threshold.
In this case that threshold appears to be 10, which is also the value of K for our problem. That should explain the name that we gave K initially. The carrying capacity or saturation level of an area is the maximum sustainable population for that area.
So, the logistics equation, while still quite simplistic, does a much better job of modeling what will happen to a population.
Now, let’s move on to the point of this section. The logistics equation is an example of an autonomous differential equation. Autonomous differential equations are differential equations that are of the form.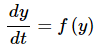
The only place that the independent variable, t in this case, appears is in the derivative.
Notice that if f (y0) = 0 for some value y=y0 then this will also be a solution to the differential equation. These values are called equilibrium solutions or equilibrium points. What we would like to do is classify these solutions. By classify we mean the following. If solutions start “near” an equilibrium solution will they move away from the equilibrium solution or towards the equilibrium solution? Upon classifying the equilibrium solutions we can then know what all the other solutions to the differential equation will do in the long term simply by looking at which equilibrium solutions they start near.
So, just what do we mean by “near”? Go back to our logistics equation.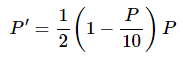
As we pointed out there are two equilibrium solutions to this equation P = 0 and P = 10 . If we ignore the fact that we’re dealing with population these points break up the P number line into three distinct regions.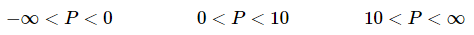
We will say that a solution starts “near” an equilibrium solution if it starts in a region that is on either side of that equilibrium solution. So, solutions that start “near” the equilibrium solution P = 10 will start in either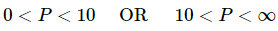
and solutions that start “near” P = 0 will start in either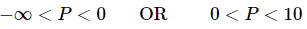
For regions that lie between two equilibrium solutions we can think of any solutions starting in that region as starting “near” either of the two equilibrium solutions as we need to.
Now, solutions that start “near” P = 0 all move away from the solution as t increases. Note that moving away does not necessarily mean that they grow without bound as they move away. It only means that they move away. Solutions that start out greater than P = 0 move away but do stay bounded as t grows. In fact, they move in towards P = 10 .
Equilibrium solutions in which solutions that start “near” them move away from the equilibrium solution are called unstable equilibrium points or unstable equilibrium solutions. So, for our logistics equation, P = 0 is an unstable equilibrium solution.
Next, solutions that start “near” P = 10 all move in toward P = 10 as t increases. Equilibrium solutions in which solutions that start “near” them move toward the equilibrium solution are called asymptotically stable equilibrium points or asymptotically stable equilibrium solutions. So, P = 10 is an asymptotically stable equilibrium solution.
There is one more classification, but I’ll wait until we get an example in which this occurs to introduce it. So, let’s take a look at a couple of examples.
Example 1: Find and classify all the equilibrium solutions to the following differential equation.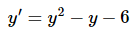
Solution: First, find the equilibrium solutions. This is generally easy enough to do.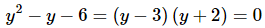
So, it looks like we’ve got two equilibrium solutions. Both y = − 2 and y = 3 are equilibrium solutions. Below is the sketch of some integral curves for this differential equation. A sketch of the integral curves or direction fields can simplify the process of classifying the equilibrium solutions.
From this sketch it appears that solutions that start “near” y = − 2 all move towards it as t increases and so y = − 2 is an asymptotically stable equilibrium solution and solutions that start “near” y = 3 all move away from it as t increases and so y = 3 is an unstable equilibrium solution.
This next example will introduce the third classification that we can give to equilibrium solutions.
Example 2: Find and classify the equilibrium solutions of the following differential equation.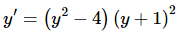
Solution: The equilibrium solutions are to this differential equation are y = − 2 , y = 2 , and y = − 1 . Below is the sketch of the integral curves.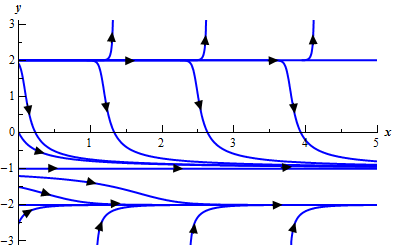
From this it is clear (hopefully) that y = 2 is an unstable equilibrium solution and y = − 2 is an asymptotically stable equilibrium solution. However, y = − 1 behaves differently from either of these two. Solutions that start above it move towards y = − 1 while solutions that start below y = − 1 move away as t increases.
In cases where solutions on one side of an equilibrium solution move towards the equilibrium solution and on the other side of the equilibrium solution move away from it we call the equilibrium solution semi-stable.
So, y = − 1 is a semi-stable equilibrium solution.
Euler’s Method
Up to this point practically every differential equation that we’ve been presented with could be solved. The problem with this is that these are the exceptions rather than the rule. The vast majority of first order differential equations can’t be solved.
In order to teach you something about solving first order differential equations we’ve had to restrict ourselves down to the fairly restrictive cases of linear, separable, or exact differential equations or differential equations that could be solved with a set of very specific substitutions. Most first order differential equations however fall into none of these categories. In fact, even those that are separable or exact cannot always be solved for an explicit solution.Without explicit solutions to these it would be hard to get any information about the solution.
So, what do we do when faced with a differential equation that we can’t solve? The answer depends on what you are looking for. If you are only looking for long term behavior of a solution you can always sketch a direction field. This can be done without too much difficulty for some fairly complex differential equations that we can’t solve to get exact solutions.
The problem with this approach is that it’s only really good for getting general trends in solutions and for long term behavior of solutions. There are times when we will need something more. For instance, maybe we need to determine how a specific solution behaves, including some values that the solution will take. There are also a fairly large set of differential equations that are not easy to sketch good direction fields for.
In these cases, we resort to numerical methods that will allow us to approximate solutions to differential equations. There are many different methods that can be used to approximate solutions to a differential equation and in fact whole classes can be taught just dealing with the various methods. We are going to look at one of the oldest and easiest to use here. This method was originally devised by Euler and is called, oddly enough, Euler’s Method. Let’s start with a general first order IVP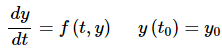 ...(1)
...(1)
where f(t,y) is a known function and the values in the initial condition are also known numbers. From the second theorem in the Intervals of Validity section we know that if f and fy are continuous functions then there is a unique solution to the IVP in some interval surrounding t = t 0 . So, let’s assume that everything is nice and continuous so that we know that a solution will in fact exist.
We want to approximate the solution to (1) near t= t0 . We’ll start with the two pieces of information that we do know about the solution. First, we know the value of the solution at t = t0 from the initial condition. Second, we also know the value of the derivative at t =t0 . We can get this by plugging the initial condition into f (t,y) into the differential equation itself. So, the derivative at this point is.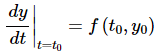
Now, recall from your Calculus I class that these two pieces of information are enough for us to write down the equation of the tangent line to the solution at t= t0 . The tangent line is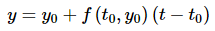
Take a look at the figure below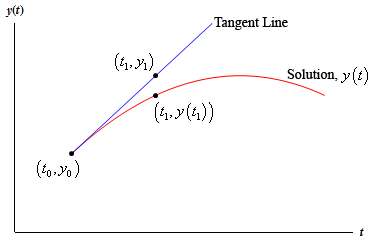
If t1 is close enough to t 0 then the point y1 on the tangent line should be fairly close to the actual value of the solution at t1 , or y(t1) . Finding y1 is easy enough. All we need to do is plug t1 in the equation for the tangent line.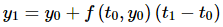
Now, we would like to proceed in a similar manner, but we don’t have the value of the solution at t1 and so we won’t know the slope of the tangent line to the solution at this point. This is a problem. We can partially solve it however, by recalling that y1 is an approximation to the solution at t1 . If y 1 is a very good approximation to the actual value of the solution then we can use that to estimate the slope of the tangent line at t1.
So, let’s hope that y1 is a good approximation to the solution and construct a line through the point (t1 , y1) that has slope f (t1 , y1). This gives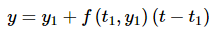
Now, to get an approximation to the solution at t = t2 we will hope that this new line will be fairly close to the actual solution at t2 and use the value of the line at t2 as an approximation to the actual solution. This gives.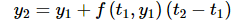
We can continue in this fashion. Use the previously computed approximation to get the next approximation. So,
In general, if we have tn and the approximation to the solution at this point, yn , and we want to find the approximation at tn + 1 all we need to do is use the following.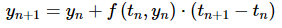
If we define fn = f(tn,yn ) we can simplify the formula to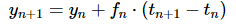 ...(2)
...(2)
Often, we will assume that the step sizes between the points t0 , t1 , t2 , … are of a uniform size of h . In other words, we will often assume that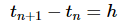
This doesn’t have to be done and there are times when it’s best that we not do this. However, if we do the formula for the next approximation becomes.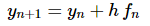 ...(3)
...(3)
So, how do we use Euler’s Method? It’s fairly simple. We start with (1) and decide if we want to use a uniform step size or not. Then starting with ( t0 , y0 ) we repeatedly evaluate (2) or (3) depending on whether we chose to use a uniform step size or not. We continue until we’ve gone the desired number of steps or reached the desired time. This will give us a sequence of numbers y1 , y2 , y3 , … y n that will approximate the value of the actual solution at t1 , t2 , t3 , … tn.
What do we do if we want a value of the solution at some other point than those used here? One possibility is to go back and redefine our set of points to a new set that will include the points we are after and redo Euler’s Method using this new set of points. However, this is cumbersome and could take a lot of time especially if we had to make changes to the set of points more than once.
Another possibility is to remember how we arrived at the approximations in the first place. Recall that we used the tangent line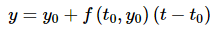
to get the value of y1 . We could use this tangent line as an approximation for the solution on the interval [t0,t1] . Likewise, we used the tangent line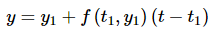
to get the value of y2 . We could use this tangent line as an approximation for the solution on the interval [ t1,t2 ] . Continuing in this manner we would get a set of lines that, when strung together, should be an approximation to the solution as a whole.
In practice you would need to write a computer program to do these computations for you. In most cases the function f(t,y) would be too large and/or complicated to use by hand and in most serious uses of Euler’s Method you would want to use hundreds of steps which would make doing this by hand prohibitive. So, here is a bit of pseudo-code that you can use to write a program for Euler’s Method that uses a uniform step size, h .
1. define f (t,y).
2. input t0 and y0.
3. input step size, h and the number of steps, n .
4. for j from 1 to n do
(a) m = f (t0,y0)
(b) y1 = y0+h∗m
(c) t1=t0+h
(d) Print t1 and y1
(e) t0 = t1
(f) y0=y1
5. end
The pseudo-code for a non-uniform step size would be a little more complicated, but it would essentially be the same.
So, let’s take a look at a couple of examples. We’ll use Euler’s Method to approximate solutions to a couple of first order differential equations. The differential equations that we’ll be using are linear first order differential equations that can be easily solved for an exact solution. Of course, in practice we wouldn’t use Euler’s Method on these kinds of differential equations, but by using easily solvable differential equations we will be able to check the accuracy of the method. Knowing the accuracy of any approximation method is a good thing. It is important to know if the method is liable to give a good approximation or not.
Example 1: For the IVP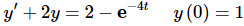
Use Euler’s Method with a step size of h = 0.1 to find approximate values of the solution at t = 0.1, 0.2, 0.3, 0.4, and 0.5. Compare them to the exact values of the solution at these points.
Solution: This is a fairly simple linear differential equation so we’ll leave it to you to check that the solution is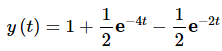
In order to use Euler’s Method we first need to rewrite the differential equation into the form given in (1).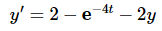
From this we can see that f (t ,y)=2−e−4t − 2y . Also note that t0 = 0 and y0 = 1 . We can now start doing some computations.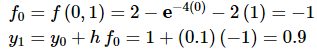
So, the approximation to the solution at t1 = 0.1 is y1 = 0.9.
At the next step we have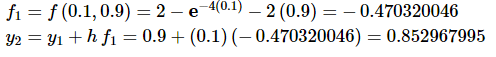
Therefore, the approximation to the solution at t2 = 0.2 is y2 = 0.852967995 .
I’ll leave it to you to check the remainder of these computations.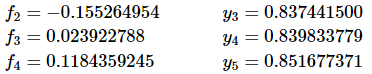
Here’s a quick table that gives the approximations as well as the exact value of the solutions at the given points.
We’ve also included the error as a percentage. It’s often easier to see how well an approximation does if you look at percentages. The formula for this is,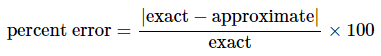
We used absolute value in the numerator because we really don’t care at this point if the approximation is larger or smaller than the exact. We’re only interested in how close the two are.
The maximum error in the approximations from the last example was 4.42%, which isn’t too bad, but also isn’t all that great of an approximation. So, provided we aren’t after very accurate approximations this didn’t do too badly. This kind of error is generally unacceptable in almost all real applications however. So, how can we get better approximations? Recall that we are getting the approximations by using a tangent line to approximate the value of the solution and that we are moving forward in time by steps of h . So, if we want a more accurate approximation, then it seems like one way to get a better approximation is to not move forward as much with each step. In other words, take smaller h ’s.
Example 2: Repeat the previous example only this time give the approximations at t=1 , t=2 , t=3 , t=4 , and t=5 . Use h = 0.1 , h = 0.05 , h = 0.01 , h = 0.005 , and h = 0.001 for the approximations.
Solution: Below are two tables, one gives approximations to the solution and the other gives the errors for each approximation. We’ll leave the computational details to you to check.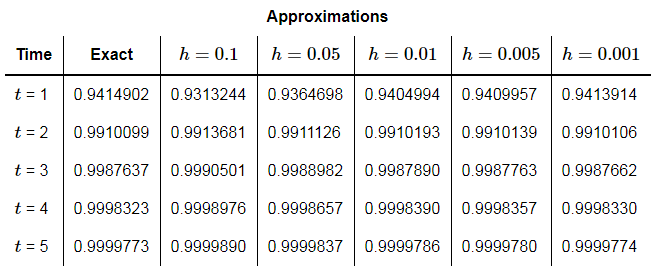
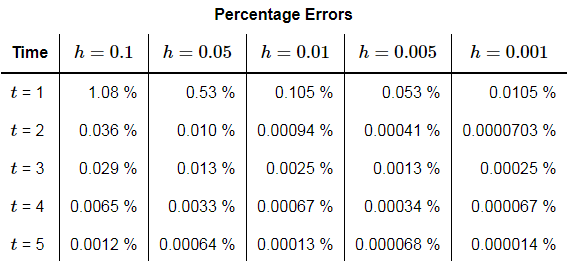
We can see from these tables that decreasing h does in fact improve the accuracy of the approximation as we expected.
There are a couple of other interesting things to note from the data. First, notice that in general, decreasing the step size, h , by a factor of 10 also decreased the error by about a factor of 10 as well.
Also, notice that as t increases the approximation actually tends to get better. This isn’t the case completely as we can see that in all but the first case the t=3 error is worse than the error at t=2, but after that point, it only gets better. This should not be expected in general. In this case this is more a function of the shape of the solution. Below is a graph of the solution (the line) as well as the approximations (the dots) for h=0.1 .
Notice that the approximation is worst where the function is changing rapidly. This should not be too surprising. Recall that we’re using tangent lines to get the approximations and so the value of the tangent line at a given t will often be significantly different than the function due to the rapidly changing function at that point.
Also, in this case, because the function ends up fairly flat as t increases, the tangents start looking like the function itself and so the approximations are very accurate. This won’t always be the case of course.
Let’s take a look at one more example.
Example 3: For the IVP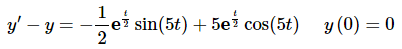
Use Euler’s Method to find the approximation to the solution at t=1,t=2,t=3,t=4,and t=5 . Use h = 0.1 , h = 0.05 , h = 0.01 , h = 0.005 , and h = 0.001 for the approximations.
Solution: We’ll leave it to you to check the details of the solution process. The solution to this linear first order differential equation is.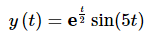
Here are two tables giving the approximations and the percentage error for each approximation.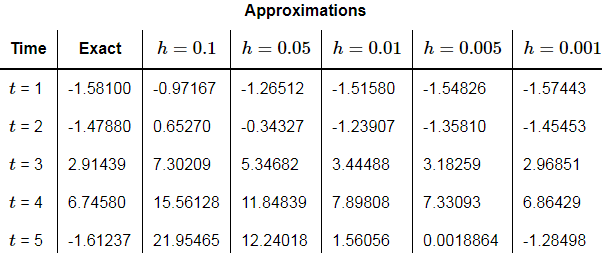
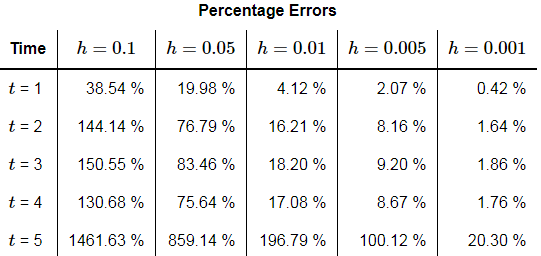
So, with this example Euler’s Method does not do nearly as well as it did on the first IVP. Some of the observations we made in Example 2 are still true however. Decreasing the size of h decreases the error as we saw with the last example and would expect to happen. Also, as we saw in the last example, decreasing h by a factor of 10 also decreases the error by about a factor of 10.
However, unlike the last example increasing t sees an increasing error. This behavior is fairly common in the approximations. We shouldn’t expect the error to decrease as t increases as we saw in the last example. Each successive approximation is found using a previous approximation. Therefore, at each step we introduce error and so approximations should, in general, get worse as t increases.
Below is a graph of the solution (the line) as well as the approximations (the dots) for h = 0.05.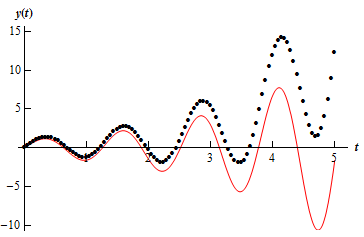
As we can see the approximations do follow the general shape of the solution, however, the error is clearly getting much worse as t increases.
So, Euler’s method is a nice method for approximating fairly nice solutions that don’t change rapidly. However, not all solutions will be this nicely behaved. There are other approximation methods that do a much better job of approximating solutions. These are not the focus of this course however, so I’ll leave it to you to look further into this field if you are interested.
Also notice that we don’t generally have the actual solution around to check the accuracy of the approximation. We generally try to find bounds on the error for each method that will tell us how well an approximation should do. These error bounds are again not really the focus of this course, so I’ll leave these to you as well if you’re interested in looking into them.
|
112 videos|65 docs|3 tests
|
FAQs on Intervals of Validity - Calculus - Mathematics
| 1. What are intervals of validity in mathematics? |  |
| 2. How do we find the intervals of validity for a given inequality? |  |
| 3. Can the intervals of validity be different for equations and inequalities? |  |
| 4. How can intervals of validity be represented graphically? |  |
| 5. Are there any specific strategies for finding intervals of validity? |  |





















