Representation of Continuous & Discrete, Time Signals -1 | Signals and Systems - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| Properties of Signals |

|
| Signal to Noise Ratio |

|
| Standard Continuous Time Signals |

|
| Classification of Continuous Time Signal |

|
| Discrete-Time Signals |

|
Properties of Signals
A signal can be classified as periodic or aperiodic; discrete or continuous time; discrete of continuous-valued; or as a power or energy signal.
(i) Periodic / Aperiodic
A signal is said to be periodic signal if it has a definite pattern and repeats itself at a regular interval of time. Whereas, the signal which does not at the regular interval of time is known as an aperiodic signal or non-periodic signal.A continuous time signal x(t) is said to be periodic if and only if:
𝑥(𝑡 + 𝑇) = 𝑥(𝑡) for − ∞ < 𝑡 < ∞
Where, T is a positive constant that represents the time period of the periodic signal. The smallest value of the time period (T) which justifies the definition of the periodic signal is known as fundamental time period of the signal and is denoted by (𝑇0).
Also,
𝑥(𝑡 + 𝑚𝑇) = 𝑥(𝑡)
Where, m is an integer. This means if the definition is satisfied for 𝑇 = 𝑇0, then it is also satisfied for 𝑇 = 2𝑇0, 𝑇 = 3𝑇0 … and so on with 𝑇0 as the fundamental time period. Therefore, the fundamental time period defines the duration of one complete cycle of the periodic signal x(t).
(ii) Symmetric / Asymmetric
There are two types of signal symmetry: odd and even.
(a) A signal x(t) has odd symmetry if and only if x(-t) = -x(t) for all t.
(b) It has even symmetry if and only if x(-t) = x(t).
(iii) Continuous and Discrete Signals and Systems
- A continuous signal is a mathematical function of an independent variable, which represents a set of real numbers.
- It is required that signals are uniquely defined in except for a finite number of points.

- A continuous time signal is one which is defined for all values of time. A continuous time signal does not need to be continuous (in the mathematical sense) at all points in time. A continuous-time signal contains values for all real numbers along the X-axis. It is denoted by x(t).
- Basically, the Signals are detectable quantities which are used to convey some information about time-varying physical phenomena. some examples of signals are human speech, temperature, pressure, and stock prices.
- Electrical signals, normally expressed in the form of voltage or current waveforms, they are some of the easiest signals to generate and process.
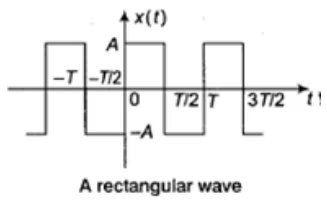
Example: A rectangular wave is discontinuous at several points but it is continuous time signal.
(iv) Discrete / Continuous-Time Signals
- A continuous time signal is defined for all values of t. A discrete time signal is only defined for discrete values of t = ..., t-1, t0, t1, ..., tn, tn+1, tn+2, ... It is uncommon for the spacing between tn and tn+1 to change with n.
- The spacing is most often some constant value referred to as the sampling rate:
Ts = tn+1 - tn - It is convenient to express discrete time signals as x(nTs)= x[n].
- That is, if x(t) is a continuous-time signal, then x[n] can be considered as the nth sample of x(t).
- Sampling of a continuous-time signal x(t) to yield the discrete-time signal x[n] is an important step in the process of digitizing a signa
(v)Energy and Power Signal
- When the strength of a signal is measured, it is usually the signal power or signal energy that is of interest.
- The signal power of x(t) is defined as:
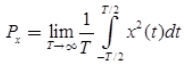
and the signal energy as:
- A signal for which Px is finite and non-zero is known as a power signal.
- A signal for which Ex is finite and non-zero is known as an energy signal.
- Px is also known as the mean-square value of the signal.
- Signal power is often expressed in the units of decibels (dB).
- The decibel is defined as
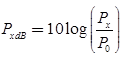 where P0 is a reference power level, usually equal to one squared SI unit of the signal.
where P0 is a reference power level, usually equal to one squared SI unit of the signal. - For example if the signal is a voltage then the P0 is equal to one square Volt.
- A Signal can be Energy Signal or a Power Signal but it can not be both. Also a signal can be neither a Energy nor a Power Signal.
- As an example, the sinusoidal test signal of amplitude A, x(t) = Asin(ωt) has energy Ex that tends to infinity and power,
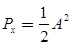 or in decibels (dB): 20log(A). The signal is thus a power signal.
or in decibels (dB): 20log(A). The signal is thus a power signal.
Signal to Noise Ratio
- Any measurement of a signal necessarily contains some random noise in addition to the signal. In the case of additive noise, the measurement is:
x(t) = s(t)+n(t)
where s(t) is the signal component and n(t) is the noise component. - The signal to noise ratio is defined as:
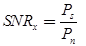 or in decibels,
or in decibels, 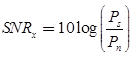
- The signal to noise ratio is an indication of how much noise is contained in a measurement.
Standard Continuous Time Signals
(a) Impulse Signal
where ∞ is the height of impulse signal having unit area.
and 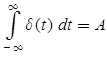 When A = 1 (unit impulse Area)
When A = 1 (unit impulse Area)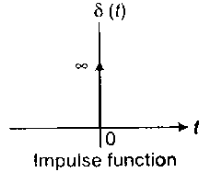
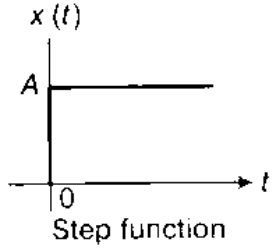
(b) Step Signal
Unit Step Signal if A = 1,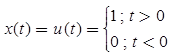
(c) Ramp Signal
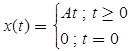
Unit Ramp Signal (A = 1)
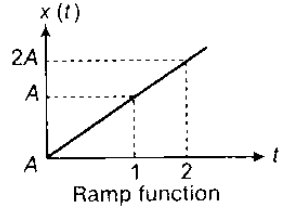
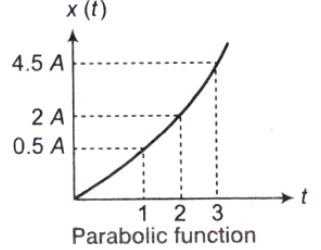
(d) Parabolic Signal
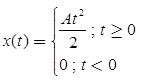
Unit Parabolic Signal when A = 1,
(e) Unit Pulse Signal
x(t) = π(t)
= u(t + 1/2) - u(t - 1/2)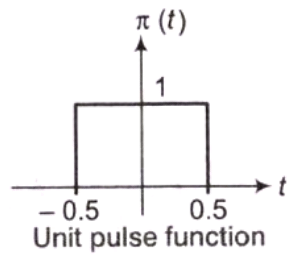
(f) Sinusoidal Signal
Co-sinusoidal Signal: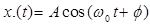
Where, 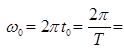 angular frequency in rad/sec
angular frequency in rad/sec
f0 = frequency in cycle/sec or Hz
T = time period in second
When 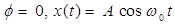
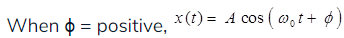
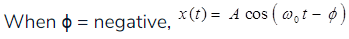
(g) Sinusoidal Signal
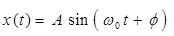
Where, 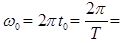 Angular frequency in red/sec
Angular frequency in red/sec
f0 = frequency in cycle/sec or Hz
T = time period in second
When 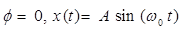
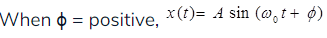
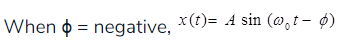
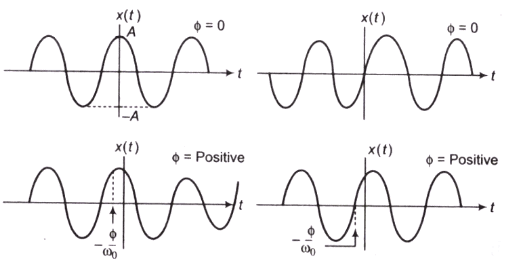
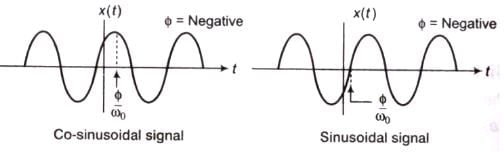
(h) Exponential Signal
- Real Exponential Signal
x(t) = Aebt: where, A and b are real.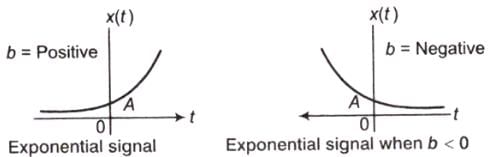
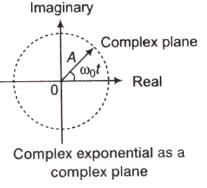
(i) Complex Exponential Signal
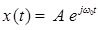
The complex exponential signal can be represented in a complex plane by a rotating vector, which rotates with a constant angular velocity of ω0 red/sec.
(j) Exponentially Rising/Decaying Sinusoidal Signal
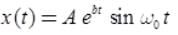
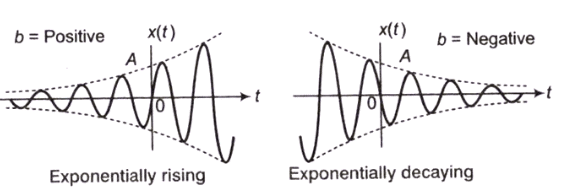
(k) Triangular Pulse Signal
(l) Signum Signal
(m) SinC Signal
(n) Gaussian Signal
Important points:
- The sinusoidal and complex exponential signals are always periodic.
- The sum of two periodic signals is also periodic if the ratio of their fundamental periods is a rational number.
- Ideally, an impulse signal is a signal with infinite magnitude and zero duration.
- Practically, an impulse signal is a signal with large magnitude and short duration.
Classification of Continuous Time Signal
The continuous time signal can be classified as:1. Deterministic and Non-Deterministic Signals
- The signal that can be completely specified by a mathematical equation is called a deterministic signal. The step, ramp, exponential and sinusoidal signals are examples of deterministic signals.
- The signal whose characteristics are random in nature is called a non-deterministic signal. The noise signal from various sources like electronic amplifiers, oscillator etc., are examples of non-deterministic signals.
- Periodic and Non-periodic Signals
- A periodic signal will have a definite pattern that repeats again and again over a certain period of time.
x(t+T) = x(t)
2. Symmetric (even) and Anti-Symmetric (odd) Signals
When a signal exhibits symmetry with respect to t = 0, then it is called an even signal.
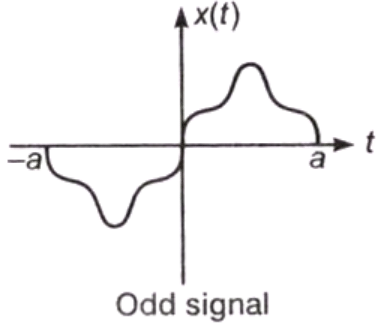
x(-t) = x(t)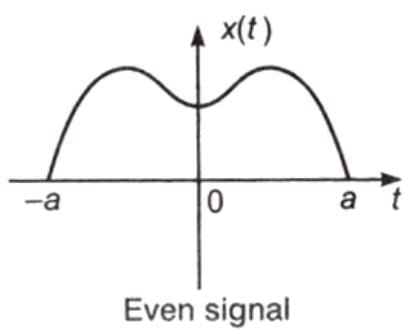 When a signal exhibits anti-symmetry with respect to t = 0, then it is called an odd signal.
When a signal exhibits anti-symmetry with respect to t = 0, then it is called an odd signal.
x(-t) = -x(t)
Let X(t) = Xe(t) + X0(t)
Where, Xe(t) = even part of X(t)
X0(t) = odd part of X(t)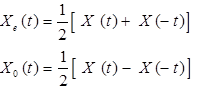
Discrete-Time Signals
The discrete signal is a function of a discrete independent variable. In a discrete time signal, the value of discrete time signal and the independent variable time are discrete. The digital signal is same as discrete signal except that the magnitude of the signal is quantized. Basically, discrete time signals can be obtained by sampling a continuous-time signal. It is denoted as x(n).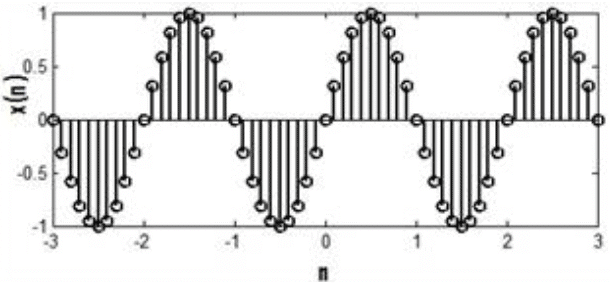
Digital Impulse Signal or Unit Sample Sequence
- Impulse signal,
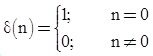
- Unit Step Signal
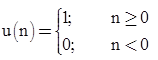
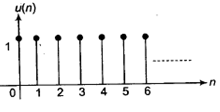
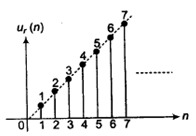
- Ramp Signal
Ramp signal,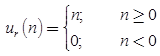
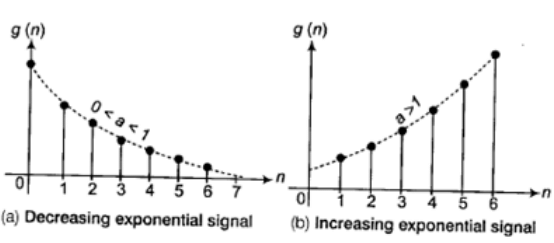
- Exponential Signal
Exponential Signal,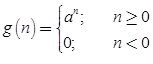
- Discrete Time Sinusoidal Signal
x[n] = A cos(ωon+ θ) ; For n in the range -∞ < n < ∝
x[n] = A sin(ωon+ θ). For n in the range -∞ < n < ∞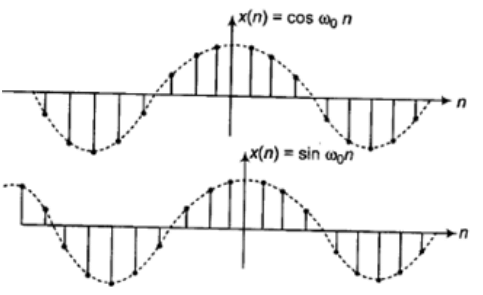
- A discrete-time sinusoid is periodic only if its frequency is a rational number.
- Discrete-time sinusoids whose frequencies are separated by an integer multiple of 2π are identical.
|
45 videos|70 docs|33 tests
|
FAQs on Representation of Continuous & Discrete, Time Signals -1 - Signals and Systems - Electrical Engineering (EE)
| 1. What is the signal-to-noise ratio? |  |
| 2. What are some examples of standard continuous time signals? |  |
| 3. How are continuous time signals classified? |  |
| 4. What is the representation of discrete-time signals? |  |
| 5. How are continuous and discrete-time signals related? |  |





















