Past Year Questions: Shear Force and Bending Moment | Solid Mechanics - Mechanical Engineering PDF Download
Q1: An idealized frame supports a load as shown in the figure. The horizontal component of the force transferred from the horizontal member PQ to the vertical member RS at P is N (round off to one decimal place). [2023, Set-II]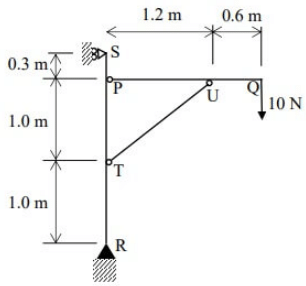
(a) 12
(b) 16
(c) 18
(d) 24
Ans: (c)
As member UT is a link member, it will carry axial load only (assuming as R).
FBD of ′PQ′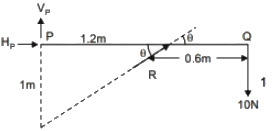
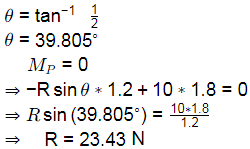
Now,
FH = 0
⇒ HP −Rcos(39.805∘) = 0
⇒ HP =23.43∗cos(39.805∘)
=17.988 N
Q2: A beam is subjected to a system of coplanar forces as shown in the figure. The magnitude of vertical reaction at Support P is N (round off to one decimal place). [2023, Set-II]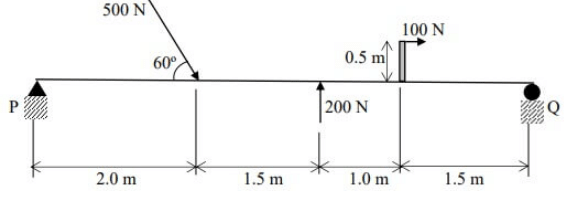
(a) 197
(b) 125.2
(c) 362.1
(d) 148.2
Ans: (a)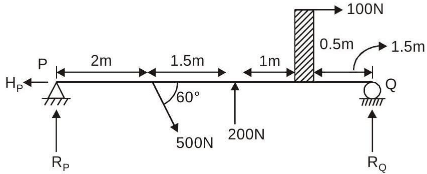 Taking components of inclined 500 N load along horizontal and vertical direction.
Taking components of inclined 500 N load along horizontal and vertical direction.
Now, using equilibrium equations.
⇒ HP = 350 N
⇒ MQ = 0 ⇒ RP ∗ 6 − (500 sin60º) ∗ 4 + 200 ∗ 2.5 + 100 ∗ 0.5 = 0
⇒ RP =197 N
Q3: Consider the beam shown in the figure (not to scale), on a hinge support at end A and a roller support at end B. The beam has a constant flexural rigidity, and is subjected to the external moments of magnitude M at one-third spans, as shown in the figure. Which of the following statements is/ are TRUE? [2023, Set-I]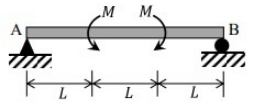 (a) Support reactions are zero
(a) Support reactions are zero
(b) Shear force is zero everywhere
(c) Bending moment is zero everywhere
(d) Deflection is zero everywhere
Ans: (a,b)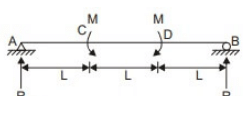
Using equilibrium equations 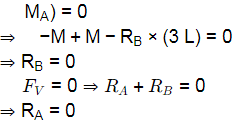
SFD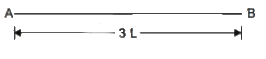 ⇒ No shear force throughout the span.
⇒ No shear force throughout the span.
BMD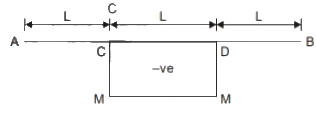
As there is BM in span CD, which leads to curvature in CD. i.e. deflection is not zero everywhere.
Q4: Joints I, J, K, L, Q and M of the frame shown in the figure (not drawn to the scale) are pins. Continuous members IQ and IJ are connected through a pin at N. Continuous members JM and KQ are connected through a pin at P. The frame has hinge supports at joints R and S. The loads acting at joints I, J and K are along the negative Y direction and the loads acting at joints I, M are along the positive X direction. [2020, Set-II]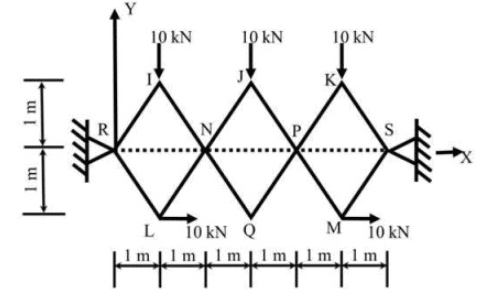 The magnitude of the horizontal component of reaction (in kN) at S, is
The magnitude of the horizontal component of reaction (in kN) at S, is
(a) 5
(b) 10
(c) 15
(d) 20
Ans: (c)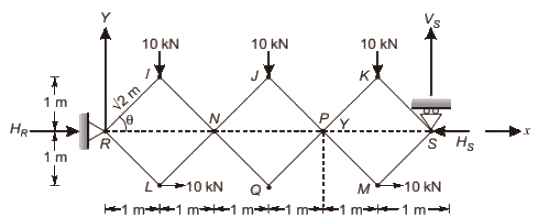 Remove hinge at support S and replace it with roller support as shown in the figure.
Remove hinge at support S and replace it with roller support as shown in the figure.
Step One : Find coordinates of all the points where forces are acting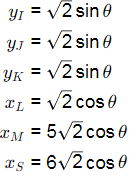
Step Two: Find virtual displacements of all the points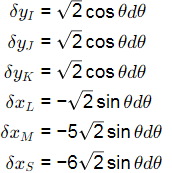
Step Three : Use principle of virtual work to find unknown horizontal force Hs
⇒ δU = 0
= [−10 × √2 cosθdθ] × 3 + [− 10 × − √2 cos θdθ] + [− 10 × −5√2 sin θdθ] − [−Hs × − 6√2 sin θdθ] 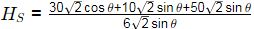
Substituting, θ = 45∘ HS = 90/6 = 15kN
Note: Sign conventions
If a force acts along positive x or positive y-axis, take it as positive.
If a force acts along negative x or negative y-axis, take it as negative.
Q5: A weightless cantilever beam of span L is loaded as shown in the figure. For the entire span of the beam, the material properties are identical and the cross-section is rectangular with constant width. [2020, Set-II]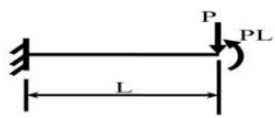 From the flexure-critical perspective, the most economical longitudinal profile of the beam to carry the given loads amongst the options given below, is
From the flexure-critical perspective, the most economical longitudinal profile of the beam to carry the given loads amongst the options given below, is
(a) 
(b) 
(c) 
(d) 
Ans: (c)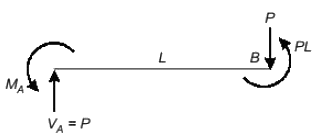
(−PL)+(PL)+(−MA) = 0
MA = 0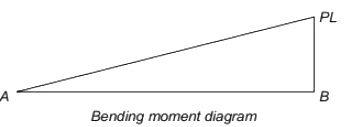 For most economical,
For most economical,
Maximum cross-section is given where maximum bending moment occurs.
Q6: A rigid weightless platform PQRS shown in the figure (not drawn to the scale) can slide freely in the vertical direction. The platform is held in position by the weightless member OJ and four weightless, frictionless rollers. Point O and J are pin connections. A block of 90 kN rests on the platform as shown in the figure. [2020, Set-I]
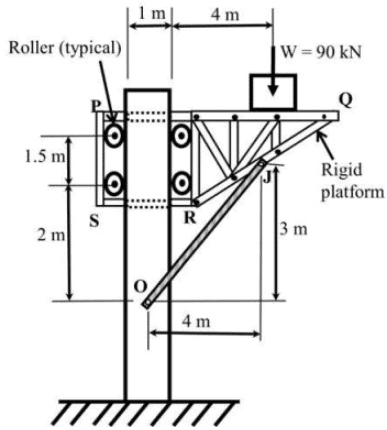 The magnitude of horizontal component of the reaction (in kN) at pin O, is
The magnitude of horizontal component of the reaction (in kN) at pin O, is
(a) 90
(b) 120
(c) 150
(d) 180
Ans: (b) Σy = 0
Σy = 0
⇒ Ro sin36.87−90 = 0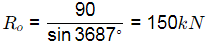
Horizontal reaction at O
Q7: Consider the three prismatic beam with the clamped supports P, Q and R as shown in the figures [2017, Set-II] Given that modulus of Elasticity, E is 2.5 × 104 ; and the moment of inertia, I is 8 × 108 mm4 , the correct Comparison of the magnitudes of the shear force S and the bending moment M developed at the supports is
Given that modulus of Elasticity, E is 2.5 × 104 ; and the moment of inertia, I is 8 × 108 mm4 , the correct Comparison of the magnitudes of the shear force S and the bending moment M developed at the supports is
(a) SP < SQ < SR; MP = MQ = MR
(b) SP = SQ > SR; MP = MQ > MR
(c) SP < SQ > SR; MP = MQ = MR
(d) SP < SQ < SR; MP < MQ < MR
Ans: (c)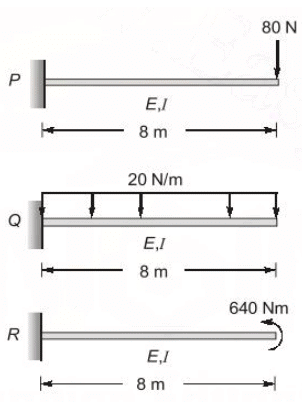
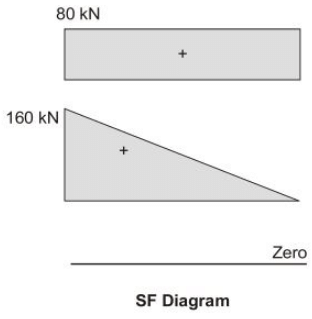
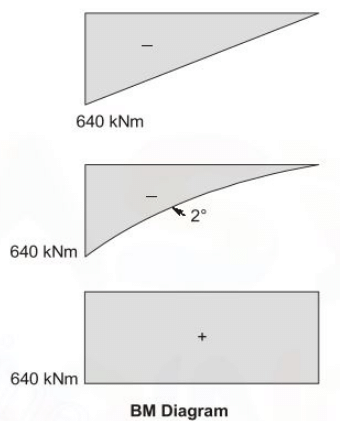
SP < SQ > SR
MP = MQ = MR
Q8: A simply supported beam is subjected to a uniformly distributed load. Which one of the following statements is true? [2017 : 1 Mark, Set-I]
(a) Maximum or minimum shear force occurs where the curvature is zero.
(b) Maximum or minimum bending moment occurs where the shear force is zero.
(c) Maximum or minimum bending moment occurs where the curvature is zero.
(d) Maximum bending moment and maximum shear force occur at the same section.
Ans: (a,b)
Q9: A rigid member ACB is shown in the figure. The member is supported at A and B by pinned and guided roller supports, respectively. A force Pacts at Cas shown. Let RAh and RBh be the horizontal reactions at supports A and B, respectively, and RAv be the vertical reaction at support A. Selfweight of the member may be ignored.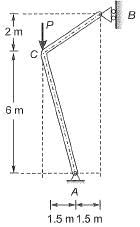 Which one of the following sets gives the correct magnitudes of RAv, RBh and RAv? [2016 : 2 Marks, Set-I]
Which one of the following sets gives the correct magnitudes of RAv, RBh and RAv? [2016 : 2 Marks, Set-I]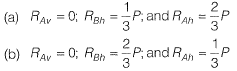
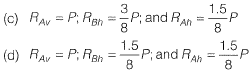
Ans: (d)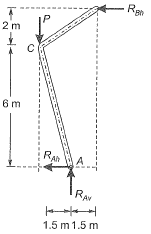
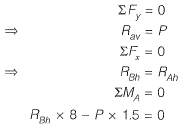

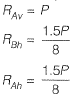
Q10: The following statement are related to bending of beams
I. The slope of the bending moment diagram is equal to the shear force.
II. The slope of the shear force diagram is equal to the load intensity.
III. The slope of the curvature is equal to the fiexural rotation.
IV. The second derivative of the deflection is equal to the curvature.
The only FALSE statement is [2012 : 1 Mark]
(a) I
(b) II
(c) III
(d) IV
Ans: (c)
We know that,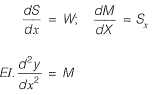
Q11: For the cantilever bracket, PQRS, loaded as shown in the a djoining figure ( PQ = RS = L, and QR = 2L), which of the following statements is FALSE? [2011 : 2 Marks]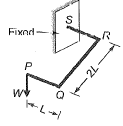 (a) The portion RS has a constant twisting moment with a value of 2WL.
(a) The portion RS has a constant twisting moment with a value of 2WL.
(b) The portion QR has a varying twisting moment with a maximum value of WL.
(c) The portion PQ has a varying bending moment with a maximum value of WL.
(d) The portion PQ has no twisting moment,
Ans: (b) Bending moment at a distance x from P, Mx = Wx Member PQ has varying BM with a maximum value of WL at Q and it has no twisting moment.
Bending moment at a distance x from P, Mx = Wx Member PQ has varying BM with a maximum value of WL at Q and it has no twisting moment.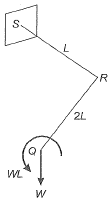 Now moment WL will act as a twisting moment for the member QR. Portion QPhas varying BM with a maximum value of 2WL at R.
Now moment WL will act as a twisting moment for the member QR. Portion QPhas varying BM with a maximum value of 2WL at R.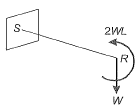 Now moment 2 Wl will act as a twisting moment for portion RS which is constant in nature.
Now moment 2 Wl will act as a twisting moment for portion RS which is constant in nature.
Q12: For the simply supported beam of length L, subjected to a uniformly distributed moment M kN-m per unit length as shown in the figure, the bending moment (in kN-m) at the mid-span of the beam is [2010 : 2 Marks] (a) Zero
(a) Zero
(b) M
(c) ML
(d) M/L
Ans: (a)
Let the reaction at the right hand support be VR upwards. Taking moments about left hand support, we get,
VR x L - ML = 0 ⇒ VR = M
Thus, the reaction at the left hand support VL will be M downwards.
∴ Moment at the mid-span
Infact the bending moment through out the beam is zero.
Q13: Two people weighing Weach are sitting on a plank of length L floating on water at L/4 from either end. Neglecting the weight of the plank, the bending moment at the centre of the plank is [2010 : 1 Mark]
(a) WL/8
(b) WL/16
(c) WL/32
(d) zero
Ans: (d)
The plank will be balanced by the buoyant force acting under its bottom. Let the intensity of buoyant force be w.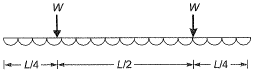 For equilibrium, w x L = W + W
For equilibrium, w x L = W + W
⇒ 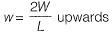
Thus, the bending moment at the centre of the plank will be,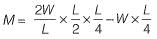
⇒ 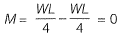
|
33 videos|72 docs|29 tests
|
FAQs on Past Year Questions: Shear Force and Bending Moment - Solid Mechanics - Mechanical Engineering
| 1. What is the difference between shear force and bending moment in structural analysis? |  |
| 2. How do you calculate shear force and bending moment for a simply supported beam? |  |
| 3. What are the common methods used to draw shear force and bending moment diagrams? |  |
| 4. What factors affect the shear force and bending moment in beams? |  |
| 5. Why is it important to analyze shear force and bending moment in structural engineering? |  |





















