Past Year Questions: Bending & Shear Stresses | Solid Mechanics - Mechanical Engineering PDF Download
Q1: The three-dimensional state of stress at a point is given by [2024, Set-l]
The maximum shear stress at the point is
(a) 25MPa
(b) 5MPa
(c) 15MPa
(d) 20MPa
Ans: (d)
In the given matrix, shear stresses are zero. So, the elements on diagonal of this matrix are principal stress. So,
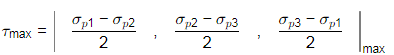
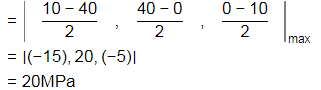
Q2: A 2D thin plate with modulus of elasticity, E = 1.0 N/m2 , and Poisson's ratio, μ = 0.5, is in plane stress condition. The displacement field in the plate is given by μ = C2y and v = 0, where us and v are displacements (in m) along the X and Y directions, respectively, and C is constant (in m−2). The distance x and y along X an Y, respectively, are in m. The stress in the X direction is σ xx =40xy N/m2 , and the shear stress is τxy = ax2 N/m2. What is the value of α (in N/m4 , in integer) ? [2023, Set-lI]
(a) 30
(b) 40
(c) 45
(d) 55
Ans: (b)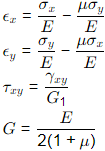
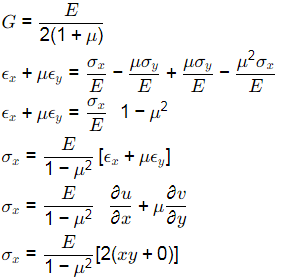

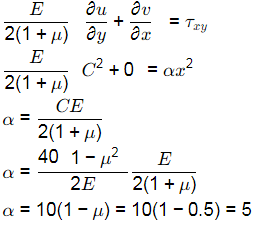
Q3: The components of pure shear strain in a sheared material are given in the matrix form: [2022, Set-lI]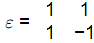
Here, Trace(ε) = 0. Given, P = Trace(ε8) and Q = Trace(ε11).
The numerical value of (P + Q) is ________. (in integer)
(a) 12
(b) 28
(c) 32
(d) 46
Ans: (c)
∣A − λI∣ = 0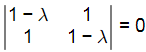
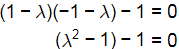
λ = ±√2
Eigen values of ε are √2 and − √2
Eigen values of ε8 are (√2)8 and (−√2)8
Eigen values of ε11 are (√2)11 and (−√2)11
P = Trace(ε8) = sum of Eigen values = (√2)8 + (−√2)8 = 32
Q = Trace(ε11) = sum of Eigen values = (√2)11 + (−√2)11
P + Q = 32 + 0 = 32
Q4: The hoop stress at a point on the surface of a thin cylindrical pressure vessel is computed to be 30.0 MPa. The value of maximum shear stress at this point is [2022, Set-I]
(a) 7.5 MPa
(b) 15.0 MPa
(c) 30.0 MPa
(d) 22.5 MPa
Ans: (a)
Given,
Hoop stress (σh) = pd/2t = 30 MPa
Maximum shear stress in plane (τmax) in plane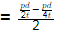 = 7.5 Mpa
= 7.5 Mpa
Q5: For a channel section subjected to a downward vertical shear force at its centroid, which one of the following represents the correct distribution of shear stress in flange and web? [2019 : 1 Mark, Set-ll]
(a)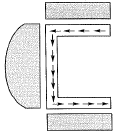
(b)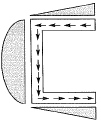
(c)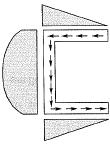
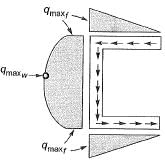
(d)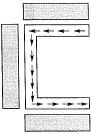
Ans: (c)
Shear flow distribution for channel.
Q6: Cross section of a built-up wooden beam as shown in figure (not drawn to scale) is subjected to a vertical shear force of 8 kN. The beam is symmetrical about the neutral axis (NA), shown, and the moment of inertia about N.A. is 1.5 x 109 mm4. Considering that the nails at the location P are spaced longitudinally (along the length of the beam) at 60 mm, each of the nails at P will be subjected to the shear force of [2019 : 2 Marks, Set-I]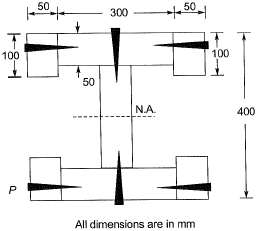 (a) 240 N
(a) 240 N
(b) 480 N
(c) 60 N
(d) 120 N
Ans: (a)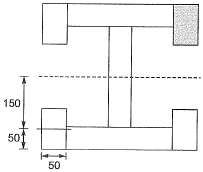 Shear Flow,
Shear Flow, 

Distance between two nails l = 60 mm
∴ S.F. resisted by each nail = q x l = 240 N
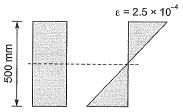
Q7: For a given loading on a rectangular plain concrete beam with an overall depth of 500 mm, the compressive strain and tensile strain developed at the extreme fibers are of the same magnitude of 2.5 x 10-4. The curvature in the beam cross-section (in m-1, round off to 3 decimal places), is _______. [2019 : 1 Mark, Set-I]
Ans:
Given: D= 500 mm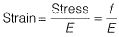
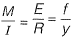
⇒ 
⇒ 
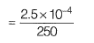
= 1*10-6
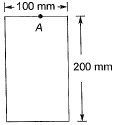
Q8: An 8 m long simply-supported elastic beam of rectangular cross-section (100 mm x 200 mm) is subjected to a uniformly distributed load of 10kN/m over its entire span. The maximum principal stress (in MPa, up to two decimal places) at a point located at the extreme compression edge of a cross-section and at 2 m from the support is ______ . [2018 : 2 Marks, Set-II]
Ans: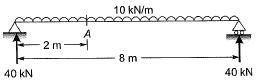
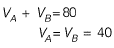
[Due to symmetry]
MA = (-10 x 2 x 1) + 40 x 2
= 60 kNm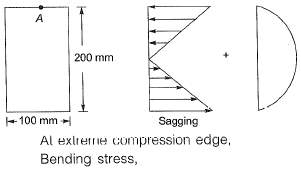 σ = My/I
σ = My/I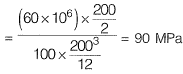
Direct shear stress = 0
Principal stress,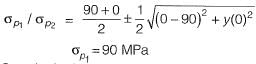
So principal stress
= 90 N/mm2 = 90 MPa
Q9: A cantilever beam of length 2 m with a square section of side length 0.1 m is loaded vertically at the free end. The vertical displacement at the free end is 5 mm. The beam is made of steel with Young’s modulus of 2.0 x 1011 N/m2. The maximum bending stress at the fixed end of the cantilever is [2018 : 2 Marks, Set-I]
(a) 20.0 MPa
(b) 37.5 MPa
(c) 60.0 MPa
(d) 75.0 MPa
Ans: (b)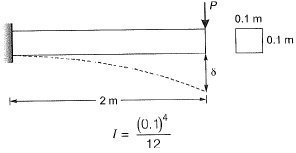
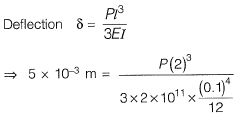
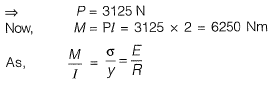
⇒ 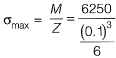
= 37.5 x 106 N/m2 = 37.5 MPa
Q10: A 450 mm long plain concrete prism is subjected to the concentrated vertical loads as shown in the figure. Cross section of the prism is given as 150 mm x 150 mm. Considering linear stress distribution across the cross-section, the modulus of rupture (expressed in MPa) is ___ . [2016 : 2 Marks, Set-II]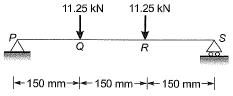 Ans:
Ans: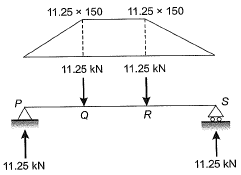 BMQ = 11.25 x 150
BMQ = 11.25 x 150
= 1.6875 x 106 N-mm
⇒ 
where, 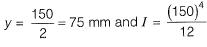
⇒ 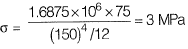
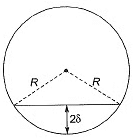
Q11: A simply supported reinforced concrete beam of length 10 m sags while undergoing shrinkage. Assuming a uniform curvature of 0.004 m-1 along the span, the maximum deflection (in m) of the beam at mid-span is ______. [2015 : 2 Marks, Set-II]
Ans:
Method - I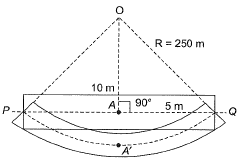 Radius,
Radius, 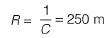
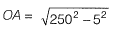
= 249.95 m
Deflection = AA' = 250 - 249.95
= 0.05 m
Method-ll
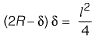
 1/R = 0.004
1/R = 0.004
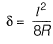
⇒
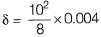
δ = 0.05 m
= 71.12N/mm2
Q12: A symmetric l-section (with width of each flange = 50 mm, thickness of web = 10 mm) of steel is subjected to a shear force of 100 kN. Find the magnitude of the shear stress (in N/mm2) in the web at its junction with the top flange _____ . [2013 : 1 Mark]
Ans:
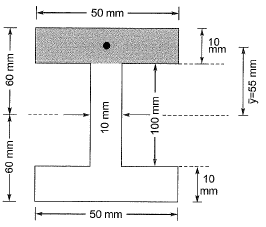
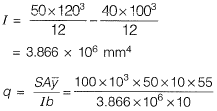
Q13: The “Plane section remain plane” assumption in bending theory implies [2013 : 1 Mark]
(a) strain profile is linear
(b) stress profile is linear
(c) both profiles are linear
(d) shear deformation is neglected
Ans: (a)
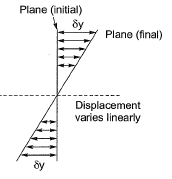 Since, E ∝ δy
Since, E ∝ δySo, strain varies linearly.
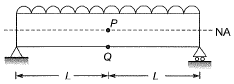
Q14: Consider a simply supported beam with a uniformly distributed load having a neutral axis (NA) as shown. For points P(on the neutral axis) and Q (at the bottom of the beam) the state of stress is best represented by which of the following pairs? [2011 : 1 Mark]
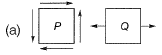
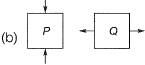
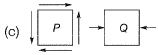
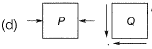
Ans: (b)
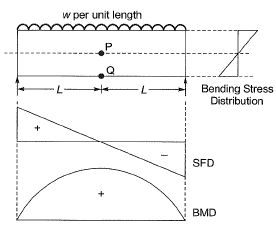 Point P: Point Plies on NA, hence bending stress is zero at point P.
Point P: Point Plies on NA, hence bending stress is zero at point P.Point Palso lies at mid span, so shear force, V = 0
⇒ Shear stress, τ = 0
∴ State of stress of point Pwill be,

Point Q: At point Q flexural stress is maximum and nature of which is tensile due to downward loading. Point Q lies at the extreme of beam, therefore, shear stress at point Q is zero.
∴ State of stress of point Q will be,

|
33 videos|72 docs|29 tests
|
FAQs on Past Year Questions: Bending & Shear Stresses - Solid Mechanics - Mechanical Engineering
| 1. What are bending stresses and how are they calculated in beams? |  |
| 2. What is shear stress and how does it differ from bending stress in structural members? |  |
| 3. How do you determine the location of maximum bending and shear stresses in a beam? |  |
| 4. What is the significance of the neutral axis in bending stress calculations? |  |
| 5. How does the material properties affect bending and shear stresses in engineering applications? |  |
















