Laplace Transforms | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE) PDF Download
Question 1: The Laplace transform F(s) of the exponential function. f(t) = eat when t > 0, where a is a constant and (s - a) > 0, is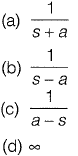
[2018 : 2 Marks, Set-II]
Answer: (b)
Solution: Taking Laplace transform, we have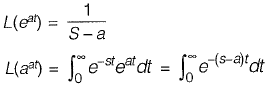
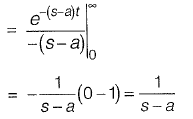
Question 2: The Laplace transform of sinh(at) is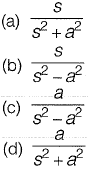 
[2019 : 1 Mark, Set-II]
Answer: (c)
Solution: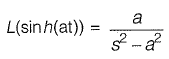
The document Laplace Transforms | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE) is a part of the Civil Engineering (CE) Course Topic wise GATE Past Year Papers for Civil Engineering.
All you need of Civil Engineering (CE) at this link: Civil Engineering (CE)
FAQs on Laplace Transforms - Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE)
| 1. What is a Laplace transform? |  |
Ans. A Laplace transform is a mathematical operation that transforms a time-domain function into a complex frequency-domain representation. It is commonly used to solve differential equations and analyze linear systems in engineering and physics.
| 2. How is a Laplace transform calculated? | |
Ans. To calculate a Laplace transform, you need to apply the integral operator to the given function. The integral is taken from zero to infinity, and the result is multiplied by the exponential term, e^(-st), where s is a complex variable representing the frequency. The resulting function is the Laplace transform of the original function.
| 3. What are the advantages of using Laplace transforms in solving differential equations? | |
Ans. Laplace transforms provide a powerful tool for solving differential equations because they convert the differential equations into algebraic equations in the frequency domain. This simplifies the problem-solving process by eliminating the need for complex differentiation and integration techniques, making it easier to find solutions.
| 4. Can Laplace transforms be used for non-linear systems? | |
Ans. The Laplace transform technique is mainly applicable to linear systems because it relies on the linearity property of the transform. However, it is possible to use approximation methods or nonlinear extensions of the Laplace transform, such as the Volterra series, to analyze and solve some non-linear systems.
| 5. Are Laplace transforms reversible? | |
Ans. Yes, Laplace transforms are reversible. The inverse Laplace transform allows us to convert a function in the frequency domain back to the time domain. By applying the inverse Laplace transform, we can obtain the original time-domain function from its Laplace transform, making it a useful tool for solving differential equations and analyzing systems.
About this Document
4.76/5
Rating
Dec 09, 2025
Last updated
Related Exams
Document Description: Laplace Transforms for Civil Engineering (CE) 2025 is part of Topic wise GATE Past Year Papers for Civil Engineering preparation.
The notes and questions for Laplace Transforms have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Laplace Transforms covers topics
like and Laplace Transforms Example, for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Laplace Transforms.
Introduction of Laplace Transforms in English is available as part of our Topic wise GATE Past Year Papers for Civil Engineering
for Civil Engineering (CE) & Laplace Transforms in Hindi for Topic wise GATE Past Year Papers for Civil Engineering course.
Download more important topics related with notes, lectures and mock test series for Civil Engineering (CE)
Exam by signing up for free. Civil Engineering (CE): Laplace Transforms | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE)
Description
Full syllabus notes, lecture & questions for Laplace Transforms | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE) - Civil Engineering (CE) | Plus excerises question with solution to help you revise complete syllabus for Topic wise GATE Past Year Papers for Civil Engineering | Best notes, free PDF download
Information about Laplace Transforms
In this doc you can find the meaning of Laplace Transforms defined & explained in the simplest way possible. Besides explaining types of
Laplace Transforms theory, EduRev gives you an ample number of questions to practice Laplace Transforms tests, examples and also practice Civil Engineering (CE)
tests
Related Searches