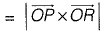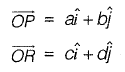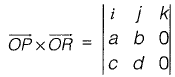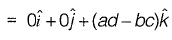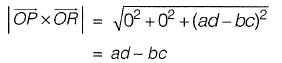Question 16: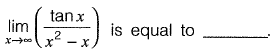 [2017 : 1 Mark, Set-I]
[2017 : 1 Mark, Set-I]
Solution: 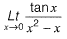 (Applying L'Hospital rule)
(Applying L'Hospital rule)
= 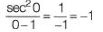
Question 17: The quadratic approximation of
f(x) = x3 - 3x2 - 5 a the point x = 0 is [2016 : 2 Marks, Set-II]
(a) 3x2 - 6x - 5
(b) -3x2 - 5
(c) -3x2 + 6x - 5
(d) 3x2 - 5
Answer: (b)
Solution: The quadratic approximation of f{x) at the point x = 0 is,
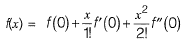
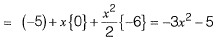
Question 18: The area between the parabola x2 = 8y and the straight line y = 8 is______. [2016 : 2 Marks, Set-II]
Solution: Parabola is x2 = 8y
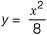 and straight is y = 0
and straight is y = 0
At the point of intersection, we have,
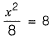
⇒ 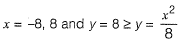
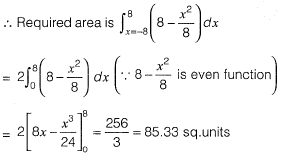
Question 19: The angle of intersection of the curves x2 = 4y and y2 = 4x at point (0, 0) is [2016 : 2 Marks, Set-II]
(a) 0°
(b) 30°
(c) 45°
(d) 90°
Answer: (d)
Solution: Given curve,
x2 = 4y .......(i)
and y2 = 4x ........(ii)
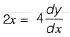
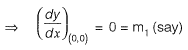
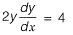
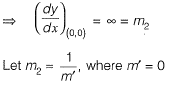
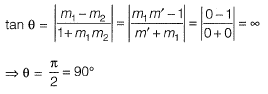
Question 20: The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is
(a) 59/6
(b) 9/2
(c) 10/3
(d) 7/6
Answer: (b)
Solution: At the point of intersection of the curves,
y = x2 + 1 and x + y = 3 i.e., y = 3 - x , we have,
x2 + 1 - 3 - x ⇒ x2 + x - 2 = 0
⇒ x = -2, 1 and 3 - x > x2 + 1
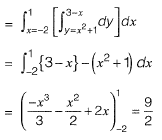
Question 21: The value of 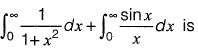 [2016 : 2 Marks, Set-I]
[2016 : 2 Marks, Set-I]
(a) π/2
(b) π
(c) 3π/2
(d) 1
Answer: (b)
Solution:
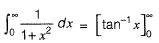
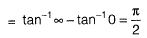
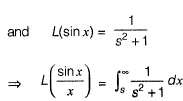
(Using "division by x")
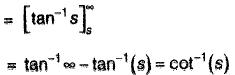
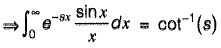
(Using definition of Laplace transform)
Put s - 0, we get
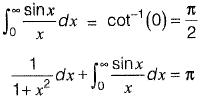
Question 22: What is the value of 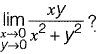 [2016 : 1 Mark, Set-II]
[2016 : 1 Mark, Set-II]
(a) 1
(b) -1
(c) 0
(d) Limit does not exit
Answer: (d)
Solution:
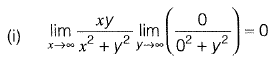
(i.e., put x = 0 and then y = 0)
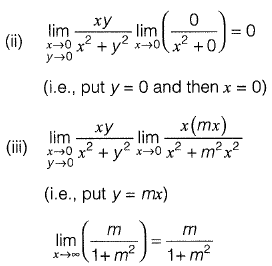
which depends on m.
Question 23: The optimum value of the function f(x) = x2 - 4x + 2 is [2016 : 1 Mark, Set-II]
(a) 2 (maximum)
(b) 2 (minimum)
(c) -2 (maximum)
(d) -2 (minimum)
Answer: (d)
Solution:
f'(x) = 0
⇒ 2x — 4 = 0
⇒ x = 2 (stationary point)
f"(x) = 2 > 0
⇒ f(x) is minimum at x = ?
i.e., (2)2 - 4(2) + 2 = -2
∴ The optimum value of f(x) is -2 (minimum)
Question 24: While minimizing the function f(x), necessary and sufficient conditions for a point x0 to be a minima are [2015 : 1 Mark, Set-II]
(a) f' (x0) > 0 and f" (x0) = 0
(b) f'(x0)< 0 an d f"(x0) = 0
(c) f' (x0) = 0 and f" (x0) < 0
(d) f' (x0) = 0 and f" (x0) > 0
Answer: (d)
Solution: f(x) has a local minimum at x = x0
if f'(x0) = 0 and f''(x0) > 0
Question 25: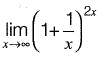 is equal to [2015 : 1 Mark, Set-II]
is equal to [2015 : 1 Mark, Set-II]
(a) e-2
(b) e
(c) 1
(d) e2
Answer: (d)
Solution:
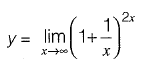
⇒ 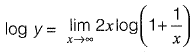
Which is in the form of 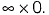
To convert this into 0/0 form, we rewrite as,
⇒ 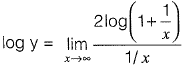
Now it is in 0/0 form.
Using L’Hospital’s rule,
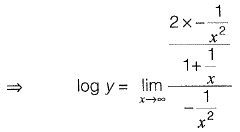
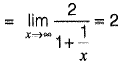
∴ y = e2
Question 26: The directional derivative of the field u(x, y, z) = x2 - 3yz in the direction of the vector 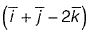 at point (2, - 1, 4) is _________. [2015 : 2 Marks, Set-I]
at point (2, - 1, 4) is _________. [2015 : 2 Marks, Set-I]
Solution: 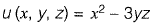
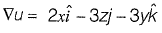
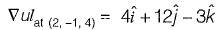
Directional derivative
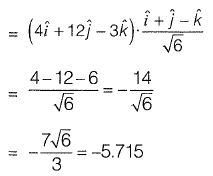
Question 27: The expression 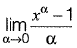 is equal to [2014 : 2 Marks, Set-II]
is equal to [2014 : 2 Marks, Set-II]
(a) ln x
(b) 0
(c) x ln x
(d) ∞
Answer: (a)
Solution:
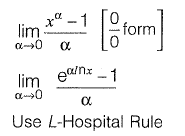
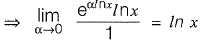
Question 28: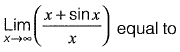 [2014 : 1 Marks, Set-I]
[2014 : 1 Marks, Set-I]
(a) -∞
(b) 0
(c) 1
(d) ∞
Answer: (c)
Solution: Put 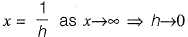
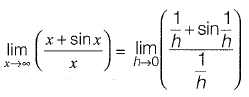
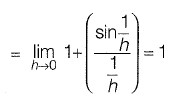
Question 29: The value of 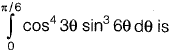 [2013 : 2 Marks]
[2013 : 2 Marks]
(a) 0
(b) 1/15
(c) 1
(d) 8/3
Answer: (b)
Solution:
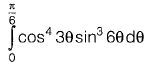
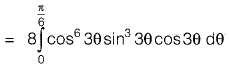
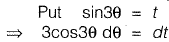
⇒ 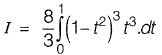
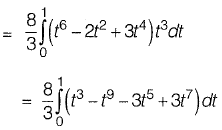
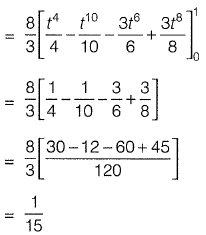
Alternative Method:
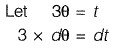
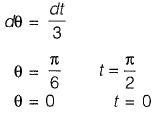
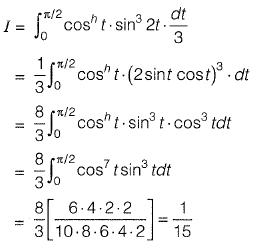
Question 30: For the parallelogram OPQR shown in the sketch, 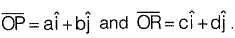 The area of the parallelogram is [2011 : 2 Marks]
The area of the parallelogram is [2011 : 2 Marks]
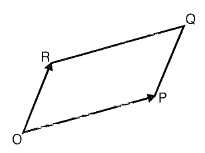
(a) ad - bc
(b) ac + bd
(c) ad + bc
(d) ab - cd
Answer: (a)
Solution:
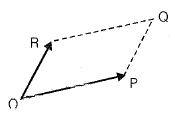
The area of parallelogram OPQR in figure shown above, is the magnitude of the vector product
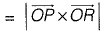
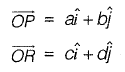
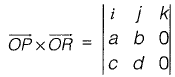
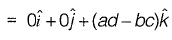
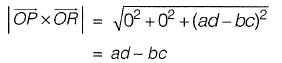
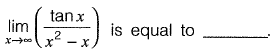 [2017 : 1 Mark, Set-I]
[2017 : 1 Mark, Set-I]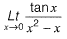 (Applying L'Hospital rule)
(Applying L'Hospital rule)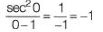
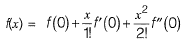
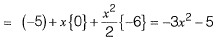
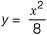 and straight is y = 0
and straight is y = 0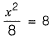
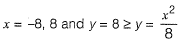
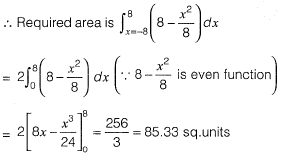
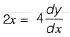
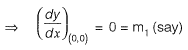
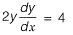
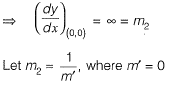
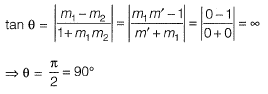
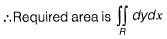
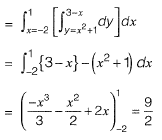
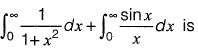 [2016 : 2 Marks, Set-I]
[2016 : 2 Marks, Set-I]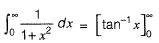
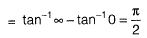
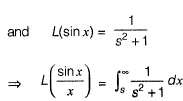
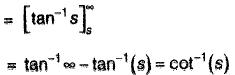
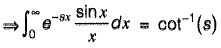
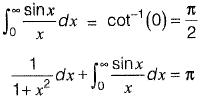
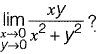 [2016 : 1 Mark, Set-II]
[2016 : 1 Mark, Set-II]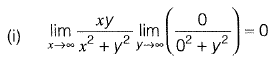
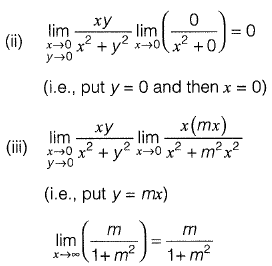
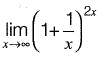 is equal to [2015 : 1 Mark, Set-II]
is equal to [2015 : 1 Mark, Set-II]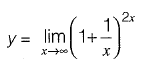
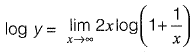
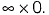
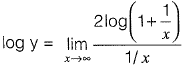
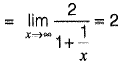
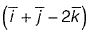 at point (2, - 1, 4) is _________. [2015 : 2 Marks, Set-I]
at point (2, - 1, 4) is _________. [2015 : 2 Marks, Set-I]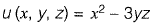
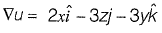
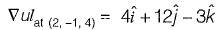
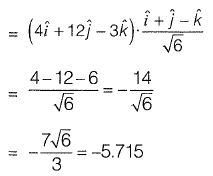
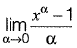 is equal to [2014 : 2 Marks, Set-II]
is equal to [2014 : 2 Marks, Set-II]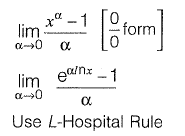
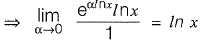
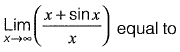 [2014 : 1 Marks, Set-I]
[2014 : 1 Marks, Set-I]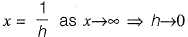
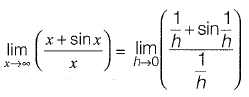
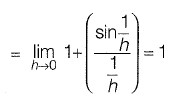
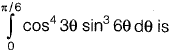 [2013 : 2 Marks]
[2013 : 2 Marks]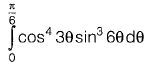
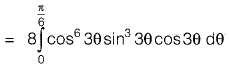
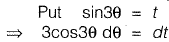
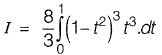
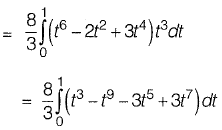

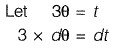
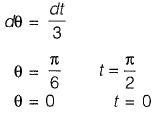
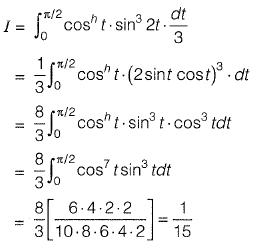
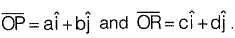 The area of the parallelogram is [2011 : 2 Marks]
The area of the parallelogram is [2011 : 2 Marks]