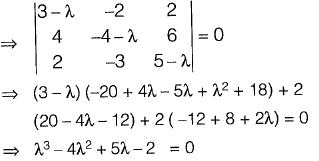Linear Algebra | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE) PDF Download
Q1: Consider two matrices 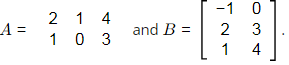
The determinant of the matrix AB is ______ (in integer). [2024, Set-ll]
Ans: 10 to 10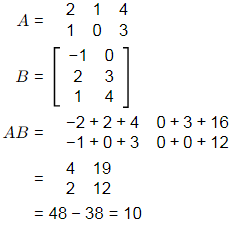 Q2: The statements P and Q are related to matrices A and B, which are conformable for both addition and multiplication.
Q2: The statements P and Q are related to matrices A and B, which are conformable for both addition and multiplication.
P : (A + B)⊤ = A⊤ + B⊤
Q : (AB)⊤ = A⊤ B⊤
Which one of the following options is CORRECT? [2024, Set-ll]
(a) Both P and Q are FALSE
(b) Both P and Q are TRUE
(c) P is FALSE and Q is TRUE
(d) P is TRUE and Q is FALSE
Ans: (d)
According to properties of a matrix
(i) (A+B)⊤ = A⊤ + B⊤
The sum of transpose of matrices is equal to the transpose of the sum of two matrices.
(ii) (AB)⊤ = B⊤ A⊤
The product of the transpose of two matrices in reverse order is equal to the transpose of the product of them.
Q3: What are the eigenvalues of the matrix 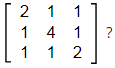 [2024, Set-l]
[2024, Set-l]
(a) -5,-1,2
(b)-5,1,2
(c) 1,3,4
(d) 1,2,5
Ans: (d)
λ1 + λ2 + λ3 = 8
λ1 λ2 λ3 = 8 = ∣A∣ = 10
Only option (A) satisfied above condition.
1 + 2 + 5 = 8
1 × 2 × 5 = 10
Q4: Cholesky decomposition is carried out on the following square matrix [A].
Let Iij and aij be the (i, j)th elements of matrices [L] and [A], respectively. If the element I22 of the decomposed lower triangular matrix [L] is 1.968 , what is the value (rounded off to the nearest integer) of the element a22 ? [2023, Set-ll]
(a) 5
(b) 7
(c) 9
(d) 11
Ans: (b)
We know, cholesky decomposition, A = LLT
Where, L= lower tringular matrix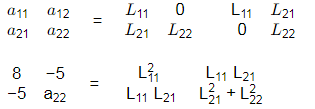
On comparison on both sides,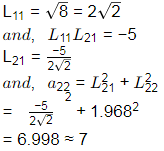
Q5: For the matrix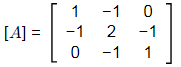
which of the following statements is/are TRUE? [2023, Set-ll]
(a) [A] {X} = {b} has a unique solution
(b) [A] {X} = {b} does not have a unique solution
(c) [A] has three linearly independent eigenvectors
(d) [A] is a positive definite matrix
Ans: (b,c)
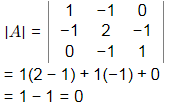
So AX = B does not have unique solution because ρ(A) < 3
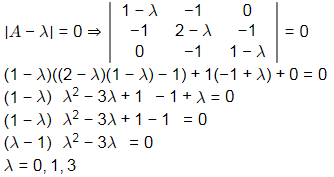
Matrix A has three distinct Eigen values so have three linearly independent eigen vectors. so option (C) is correct. Given matrix is symmetric matrix with real value entries. Hence A is not a positive definite matrix. because
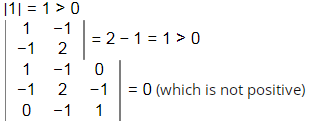
Hence option (D) is incorrect.
Q6: For the matrix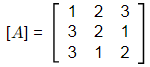
Which of the following statements is/are TRUE? [2023, Set-l]
(a) The eigenvalues of [A] T are same as the eigenvalues of [A]
(b) The eigenvalues of [A]−1 are the reciprocals of the eigenvalues of [A]
(c) The eigenvectors of [A]T are same as the eigenvectors of [A]
(d) The eigenvectors of [A]−1 are same as the eigenvectors of [A]
Ans: (a, b, c, d)
Ax = λx… (i)
ATx = λx… (ii)
A and AT both have same eigen values and eigen vectors.
Ax = λx…(i)
⇒ A−1 Ax = A−1 (λx) = λA−1 x
⇒ x = λ A−1 x
So, eigen value and eigen vector of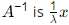 and x.
and x.
Q7: If M is an arbitrary real n × n matrix, then which of the following matrices will have non-negative eigenvalues? [2024, Set-l]
(a) M2
(b) MMT
(c) MT M
(d) (MT)2
Ans: (a, b, c, d)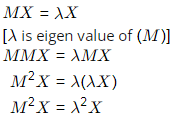
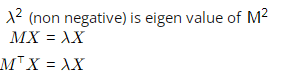
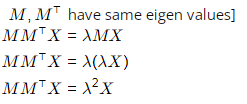
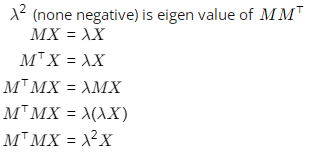
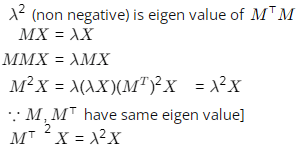
[λ2 is eigen value of (M⊤)2 which non negative] Hence, option A, B, C, D are correct.
Q8: Let y be a non-zero vector of size 2022 x 1. Which of the following statement(s) is/are TRUE? [2022, Set-ll]
(a) yyT is a symmetric matrix.
(b) yTy is an eigenvalue of yyT
(c) yyT has a rank of 2022.
(d) yyT is invertible.
Ans: (a,b)
Let vector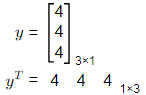
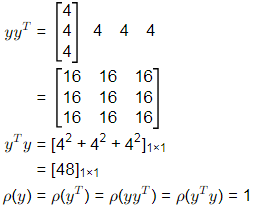
From above information
yyT is asymmetric.
yTy is an eigen value of yyT.
yyT has rank 1
det(yyT) = 0 so, yyT is not invertible.
Q9: P and Q are two square matrices of the same order. Which of the following statement(s) is/are correct? [2022, Set-ll]
(a) If P and Q are invertible, then [PQ]−1 =Q−1 P−1
(b) If P and Q are invertible, then [QP]−1 =P −1 Q−1
(c)If P and Q are invertible, then [PQ]−1 = Q−1 P−1
(d) If P and Q are not invertible, then [PQ]−1 = P−1 Q−1
Ans: (a, b)
If P and Q are invertible then (PQ)−1 = Q−1 P−1 is correct. Let,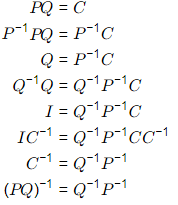
Hence, proved. Similarly, we can prove if P, Q are invertible then (QP)−1 = P−1 Q −1
Q10: The matrix M is defined as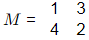 and has eigenvalues 5 and -2. The matrix Q is formed as Q = M3 − 4M2 − 2M
and has eigenvalues 5 and -2. The matrix Q is formed as Q = M3 − 4M2 − 2M
Which of the following is/are the eigenvalue(s) of matrix Q ? [2022, Set-l]
(a)15
(b) 25
(c) -20
(d) -30
Ans: (a, c)
Eigen values of M are 5, -2. So, eigen value of Q = M3 − 4M2 −2M are
53 − 4 × 52 − 2 × 5 = 15
(−2)3 − 4 × (−2)2 − 2 × (−2) =−20
Q11: The smallest eigenvalue and the corresponding eigenvector of the matrix 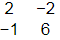 , respectively, are [2021, Set-ll]
, respectively, are [2021, Set-ll]
(a) 1.55 and 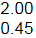
(b) 2.00 and 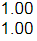
(c) 1.55 and 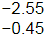
(d) 1.55 and 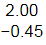
Ans: (a)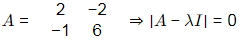

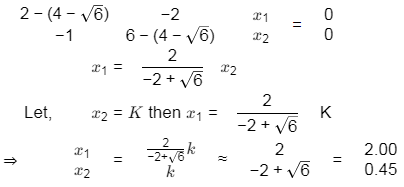
Q12: If A is a square matrix then orthogonality property mandates [2021, Set-ll]
(a) AAT= I
(b) AAT = 0
(c) AAT= A−1
(d) AAT = A2
Ans: (a)
If, AA⊤ = I or A−1 = AT
The matrix is orthogonal.
Q13: The rank of the matrix 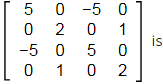 [2021, Set-ll]
[2021, Set-ll]
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (c)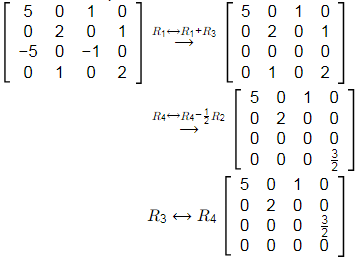
Rank(A) = 3
Q14: If P =  and Q =
and Q = 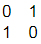 then QTPT is [2021, Set-l]
then QTPT is [2021, Set-l]
(a) 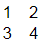
(b) 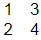
(c) 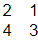
(d) 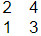
Ans: (d)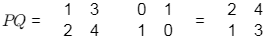
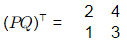
Now using Reversal law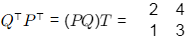
Q15: The rank of matrix 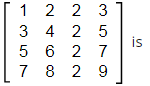 [2021, Set-l]
[2021, Set-l]
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)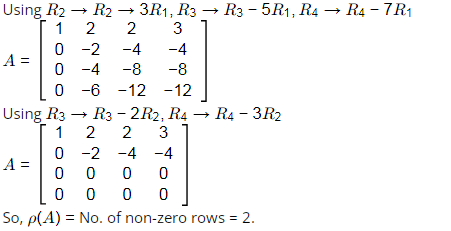
Q16: A 4x4 matrix [P] is given below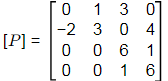
The eigen values of [P] are [2020, Set-ll]
(a) 0,3,6,6
(b) 1,2,3,4
(c) 3,4,5,7
(d) 1,2,5,7
Ans: (d)
|P|= 70 and Trace (P) = 15
So, only option, (1, 2, 5, 7) satisfies.
Q17: Consider the system of equations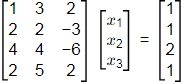
The value of x3 (round off to the nearest integer), is _______. [2020, Set-l]
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (c)
Q18: Consider the hemispherical tank of radius 13 m as shown in the figure (not drawn to scale). What is the volume of water (in m3) when the depth of water at the centre of the tank is 6 m? [2019: 2 Marks, Set-ll]
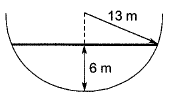
(a) 156π
(b) 396π
(c) 468π
(d) 78π
Ans: (b)
Volume of water
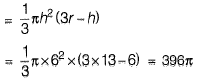
Q19: The inverse of the matrix  [2019: 2 Marks, Set-ll]
[2019: 2 Marks, Set-ll]
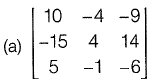
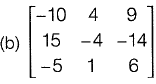
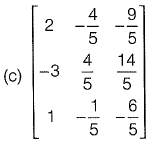
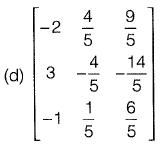
Ans: (d)
Q20: The rank of the following matrix is 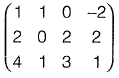 [2018 : 2 Marks, Set-II]
[2018 : 2 Marks, Set-II]
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)
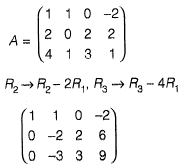
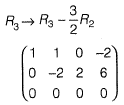
Number of non zero rows = 2
Rank of A = 2
Q21: The matrix 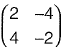 has [2018 : 2 Marks, Set-II]
has [2018 : 2 Marks, Set-II]
(a) real eigenvalues and eigenvectors
(b) real eigenvalues but complex eigenvectors
(c) complex eigenvalues but real eigenvectors
(d) complex eigenvalues and eigenvectors
Ans: (d)
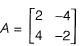

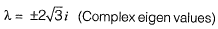
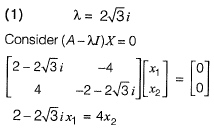
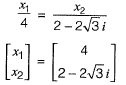
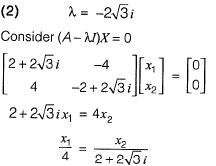

∴Complex Eigenvalues and complex Eigen vectors.
Q22: Which one of the following matrices is singular? [2018: 1 Marks, Set-I]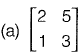
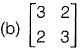
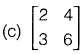
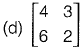
Ans: (c)
Option (a): |A| = 6 - 5 = 1
Option (b): |A| = 9 - 4 = 5
Option (c): |A| = 12-12 = 0
Option (d): |A| = 8 - 18 = -10
Hence matrix (c) is singular.
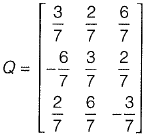
The inverse is
Q23: If A =  and B =
and B = 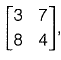 ABT is equal to [2017 : 2 Marks, Set-II]
ABT is equal to [2017 : 2 Marks, Set-II]
Ans: (a)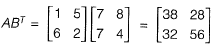
Q24: Consider the following simultaneous equations (with c1 and c2 being constants): [2017 : 1 Mark, Set-II]
3x1 + 2x2 = c1
4x1 + x2 = c2
The characteristics equation for these simultaneous equations is
(a) λ2 - 4λ - 5 = 0
(b) λ2 - 4λ + 5 = 0
(c) λ2 + 4λ - 5 = 0
(d) λ2 + 4λ + 5 = 0
Ans: (a)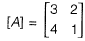
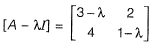
|A - λI| = 0
(3 - λ) (1 - λ) - 8 = 0
3 - 4λ + λ2 - 8 = 0
λ2 - 4λ - 5 = 0
Q25: The matrix P is the inverse of a matrix Q. If I denotes the identity matrix, which one of the following options is correct? [2017: 1 Mark, Set-I]
(a) PQ = I but QP ≠ I
(b) QP = I but PQ ≠ I
(c) PQ = I and QP = I
(d) PQ = QP = I
Ans:(c)
Given that P is inverse of Q.
P = Q-1
PQ = Q-1Q, QP = QQ-1
PQ = I , QP = I
∴ PQ = QP = I
x + 2y - 3z = a
2x + 3y + 3x = b
5x + 9y - 6z = c
This system is consistent if a, b and c satisfy the equation
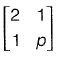 have a ratio of 3 : 1 for p = 2. What is another value of p for which the Eigenvalues have the same ratio of 3 : 1?
have a ratio of 3 : 1 for p = 2. What is another value of p for which the Eigenvalues have the same ratio of 3 : 1?
[2015: 2 Marks, Set-II]
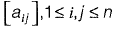 with n > 3 and aij = i.j. The rank of A is [2015 : 1 Mark, Set-II]
with n > 3 and aij = i.j. The rank of A is [2015 : 1 Mark, Set-II]
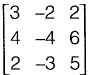 [2015 : 2 Marks, Set-I]
[2015 : 2 Marks, Set-I]
Q26: For what value of p the following set of equations will have no solution? [2015 : 1 Mark, Set-I]
2x + 3y = 5
3x + py = 10
Ans: Given system of equations has no solution if the lines are parallel i.e., their slopes are equal
2/3 = 3/p
⇒ p = 4.5
Q27: The rank of the matrix  is _____. [2014 : 2 Marks, Set-II]
is _____. [2014 : 2 Marks, Set-II]
Ans: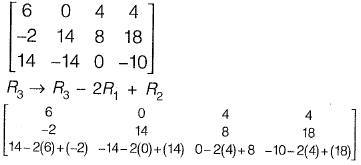
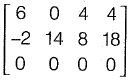
Determinant of matrix 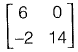 is not zero.
is not zero.
∴ Rank is 2
Q28: The determinant of matrix 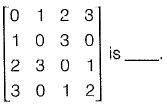 [2014 : 1 Mark, Set-II]
[2014 : 1 Mark, Set-II]
Ans: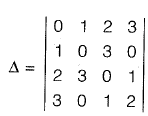
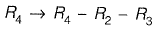
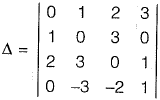
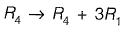
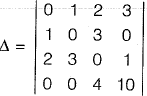
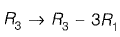

Interchanging column 1 and column 2 and taking transpose,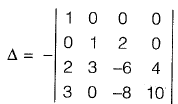
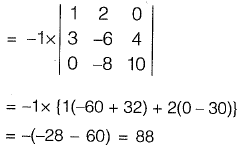
Q29: With reference to the conventional Cartesian (x, y) coordinate system, the vertices of a triangle have the following coordinates; (x1, y1) = (1, 0); (x2, y2) = (2, 2); (x3, y3) = (4, 3). The area of the triangle is equal to [2014 : 1 Mark, Set-I]
(a) 3/2
(b) 3/4
(c) 4/5
(d) 5/2
Ans: (a)
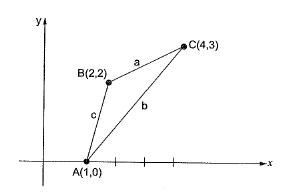
Area of triangle is
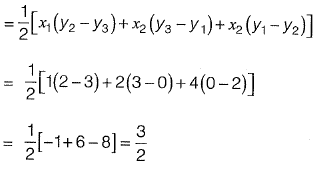
Q30: The sum of Eigen values of matrix, [M] is where 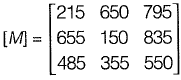 [2014 : 1 Mark, Set-I]
[2014 : 1 Mark, Set-I]
(a) 915
(b) 1355
(c) 1640
(d) 2180
Ans: (a)
Sum of eigen values = trace of matrix
= 215 + 150 + 550 = 915
Q31: Given the matrices 
 the product KT JK is ____. [2014 : 1 Mark, Set-I]
the product KT JK is ____. [2014 : 1 Mark, Set-I]
Ans:
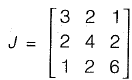
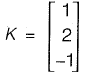
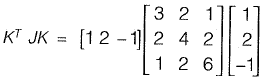
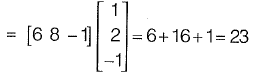
Q32: There are three matrixes P(4 x 2), Q(2 x 4) and R(4 x 1). The minimum of multiplication required to compute the matrix PQR is [2013 : 1 Mark]
Ans:If we multiply QR first then,
Q1:2x4 x R(4x1) having multiplication number 8.
There fore P(4 x 2) QR(2 x 1) will have minimum number of multiplication = (8 + 8) = 16.
Q33: The eigen values of matrix 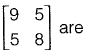 [2011 : 2 Marks]
[2011 : 2 Marks]
(a) -2.42 and 6.86
(b) 3.48 and 13.53
(c) 4.70 and 6.86
(d) 6.86 and 9.50
Ans: (b)
We need eigen values of 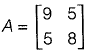
The characteristic equation is,
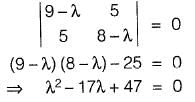
So eigen values are,
λ = 3.48, 13.53
Q34: [A] is square matix which is neither symmetric nor skew-symmetric and [A]T is its transpose. The sum and difference of these matrices are defined as [S] = [A] + [A]T and [D] = [A] - [A]T, respectively. Which of the following statements is TRUE? [2011 : 1 Mark]
(a) Both [S] and [D] are symmetric
(b) Both [S] and [D] are skew-symmetric
(c) [S] is skew-symmetric and [D] is symmetric
(d) [S] is symmetric and [D] is skew-symmetric
Ans: (d)
Since (A + At) = At + (At)t
= At + A
i.e. St = S
∴ S is symmetric
Since (A - At)t = At - (At)t
= At - A = -(A - At)
i.e. Dt = - D
So D is Skew-Symmetric.
Q35: The inverse of the matrix 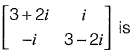 [2010 : 2 Marks]
[2010 : 2 Marks]
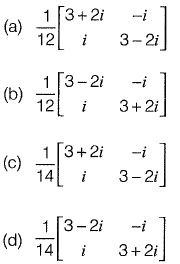
Ans: (b)
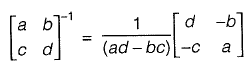
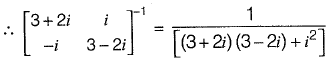
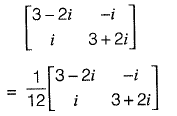
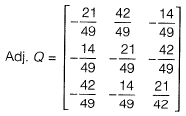
FAQs on Linear Algebra - Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE)
| 1. What are the key topics in Linear Algebra that I should study for the GATE exam? |  |
| 2. How can I effectively prepare for the Linear Algebra section of the GATE exam? |  |
| 3. What types of questions can I expect from Linear Algebra in the GATE exam? |  |
| 4. Are there any important formulas in Linear Algebra that I should memorize for the GATE exam? |  |
| 5. How much weight does Linear Algebra carry in the GATE exam compared to other subjects? |  |


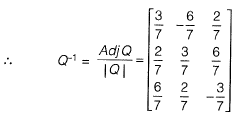
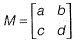
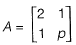
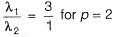
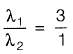
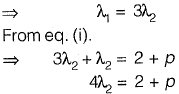
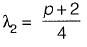
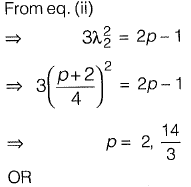
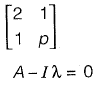
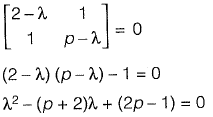
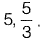 .
.