Class 10 Mathematics: CBSE Sample Question Paper (2019-20) - 4 | Mathematics (Maths) Class 10 PDF Download
Class X
Mathematics – Standard (041)
Sample Question Paper 2019-20
Max. Marks: 80 Duration : 3 hrs General Instructions: (i) All the questions are compulsory. (ii) (iii) Section A comprises of 20 questions of 1 mark each. Section B comprises of 6 questions of 2 marks each. Section C comprises of 8 questions of 3 marks each. Section D comprises of 6 questions of 4 marks each. (iv) There is no overall choice. However, an internal choice has been provided in two questions of 1 mark each, two questions of 2 marks each, three questions of 3 marks each, and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions. (v) Use of calculators is not permitted.
Section A
Q.1. 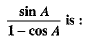 (1 Mark)
(1 Mark)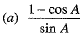
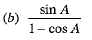
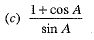
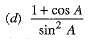
Ans. Choice (c) is correct.
We have,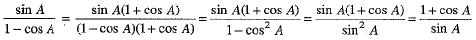
Q.2. When a solid is converted from one shape another, the volume of the new shape (1 Mark)
(a) remains the same
(b) decrease
(c) increases 4 times
(d) increases 2 times
Ans. (a) A solid’s volume remains the same
Q.3. The median of the data from the graph given in the figure is : 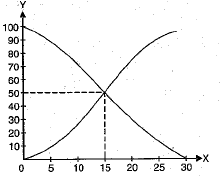
(a) 10
(b) 25
(c) 15
(d) 50
Ans. (c)
[The x-coordinate of the point of intersection of more than type and less than type o give is the required median]
Q.4. The distance of the point P (-6,8) from the origin is : (1 Mark)
(a) 8
(b) 2√7
(c) 10
(d) 6
Ans. (c)
Explanation : Distance between two points (x1, y1) and (x2, y2) is given as,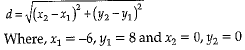
So, distance between P (-6,8) and origin O (0,0) is given by,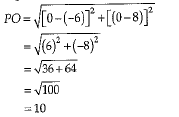
Q.5. The number of terms in the A.P. 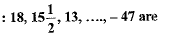
(a) 26
(b) 27
(c) 28
(d) 29
Ans. Choice (b) is correct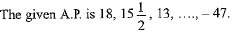
First term, a = 18, and common difference, 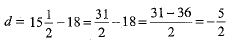 and last term (an)=-47
and last term (an)=-47
Let number of terms be n.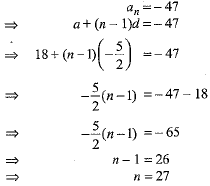
Hence, the number of terms in the given A.P. are 27.
Q.6. If one of the zeroes of a quadratic polynomial (k -1)x2 + kx +1 is - 3, then the value of k is
(a) 4/3
(b) -4/3
(c) 2/3
(d) -2/3
Ans. (a)
Let p(x) = (k - h)x2 + kx + 1
Since, - 3 is a zero of polynomial,
∴ p(-3) = 0
∴ (k-1) (-3)2 + k(-3) + 1 = 0
=> 9(k-1 )-3k + 1 = 0
=> 9k - 9 - 3k + 1=0
=> 6k - 8 = 0
=>6k = 8
∴ 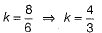
Q.7. If tan 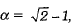 then sec2α = (1 Mark)
then sec2α = (1 Mark)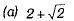
(b) 4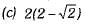
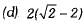
Ans. (c)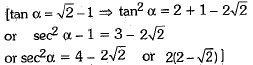
Q.8. If the sum of the circumferences of two circles with radii R1 and R2 is equal to the circumference of a circle of radius R, then : (1 Mark)
Ans. (a) R1 + R2 = R
(b) R1+ R2 > R
(c) R1 + R2 < R
(d) Nothing definite can be said about the relation among R1 R2 and R
Ans. Correct option : (a)
Explanation: According to question, Circumference of circle = Circumference of first circle + Circumference of second circle 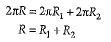
Q.9. State whether the following statements are True or False : (1 Mark)
If tan θ = 3/2, then the value of 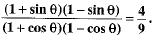
Ans. True.
Q.10. If PA and PB are two tangents to a circle with centre O such that ∠AOB = 150º, then ∠APB=? (1 Mark)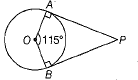
(a) 90°
(b) 60°
(c) 65°
(d) 55°
Ans. (c) Given, ∠OAP = 90
∠OBP = 90°
∴ ∠AOB + ∠APB = 180°
⇒ 115° + ∠APB = 180°
⇒ ∠APB = (180° - 115°) = 65°
Q.11. The length of the diagonal of the cuboid = _________. (1 Mark)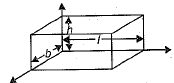
Ans. Length of the diagonal = 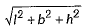
Q.12. What is the frustum of a right circular cone of height 16 cm with radii of its circular ends as 8 cm and 20 cm has slant height equal to ? (1 Mark)
Ans. 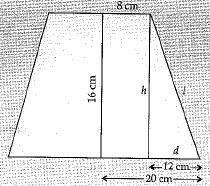
Slant height of the frustum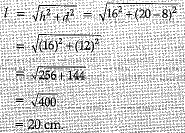
Q.13. The following questions consist of two statements - Assertion (A) and Reason (R). Answer these questions selecting the appropriate option given below : (1 Mark)
(a) Both A and R are true and R is the correct explanation for A.
(b) Both A and R are true and R is not the correct explanation for A.
(c) A is true but R is false.
(d) A is false but R is true.
Assertion ( A) : The equation 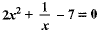 is a quadratic equation.
is a quadratic equation.
Reason (R) : Degree of quadratic equation is 2.
Ans. Choice (d) is correct.
The given equation is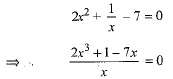
⇒ 2x3 + 1 - 7x = 0, which is not a quadratic equation.
Q.14. The longest diameter of a cone, which can be fully fitted in a cube of edge 8 cm, is_______. (1 Mark)
Ans. 8 cm; The diameter of the largest cone that can be fully fitted in a cube will be equal to the edge of the cube.
Q.15. Arun has a cubical block with one word written on each face ‘COME TO LEARN GO TO SERVE’. The block is thrown, the probability of getting ‘TO’ = ________. (1 Mark)
Ans. 1/3
[Number of possible outcomes = 6 ;
Number of favourable outcomes = 2
Required probability = 2/6 =1/3]
Q.16. Find the area of the triangle with vertices (0,0) (6,0) and (0,5) (1 Mark)
Ans. Area of triangle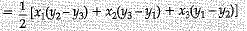
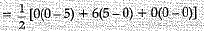
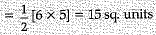
Q.17. Find a rational number between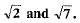 (1 Mark)
(1 Mark)
Ans. We know that 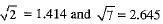
∴ 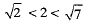
Clearly, 2 is a rational number and it lies between 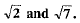
Q.18. The angle of elevation of the sun when the shadow of a 10 m long pole is 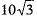 m is (1 Mark)
m is (1 Mark)
Ans.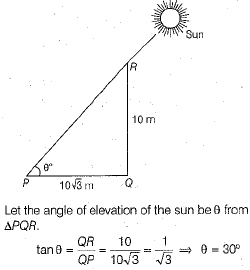
Q.19. How many irrational numbers lie between 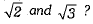 Write any two of them. (1 Mark)
Write any two of them. (1 Mark)
Ans. Infinite irrational numbers lie between 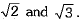 We know that
We know that
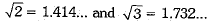 Thus, two irrational numbers lie between
Thus, two irrational numbers lie between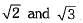 are 1.4242242224 ... and 1.5050050005.
are 1.4242242224 ... and 1.5050050005.
Q.20. If the HCF of 65 and 117 is expressible in the form 65m -117, find the value of m : (1 Mark)
Ans. By the Euclid's division algorithm, HCF of (65, 117) = 13
Since 65m -117 = 13 => m = 2
Section B
Q.21. How many multiples of 4 lie between 10 and 205 ? (2 Mark)
Ans. Multiples o f 4 lying between 10 and 205 are 12, 16, 20 , ..... , 204.
It is an A.P. with first term, a — 12, common difference, d = 4 and last term = 204.
Let number of terms be n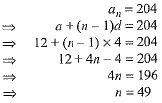
Hence, the number of multiples of 4 between 10 and 205 are 49.
Or
Determine the A.F. whose third term is 16 and 7th term exceeds the 5th term by 12.
Ans. Let a and d be the first term and common difference of the A.P. It is given that 7th term exceeds 5th term by 12
∴ a7 - a5 = 12
⇒ {a + (7 - 1)d} - {a + (5 - 1 )d} = 12 [∵ an= a + (n - 1)d]
⇒ (a + 6d) - (a + 4d) = 12
⇒ 2d = 12
⇒ d = 6 ...(1)
and a3 = 16
⇒ a + (3-1)d = 16
⇒ a + 2 x 6 = 16 [using(1)]
⇒ a = 16 - 12
⇒ a = 4 ...(2)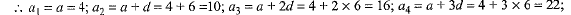
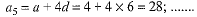
The A.P. is 4, 10,16, 22, 28.........
Q.22. Show that 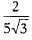 is an irrational number.
is an irrational number.
Or
Show that 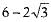 is irrational. (2 Mark)
is irrational. (2 Mark)
Ans. Let us assume that 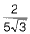 is a rational number.
is a rational number.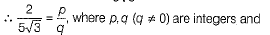 p,q are coprimes. ...(i)
p,q are coprimes. ...(i)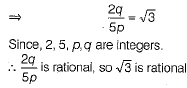
But this contradicts the fact that 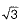 is irrational.
is irrational.
Hence 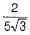 is an irrational number.
is an irrational number.
Hence proved. (1)
Or
Let us assume that 6-2√3 is rational number.
Then, it will be of the form a/b where a, b are coprime integers and b ≠ 0.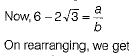
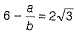 ...(1)
...(1)
Since, 6 and a/b are rational. So, their difference will be rational.
∴ 2 and √3 are rational.
As 2 is rational, so it is true.
But we know that, √3 is irrational.
So, this contradicts the fact that √3 is irrational. Therefore, our assumption is wrong.
Hence, 6 - 2√3 is irrational
Hence proved. (1)
Q.23. In the given figure, 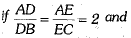 ar (ΔABC) = 36 cm2. Find the area of quadrilateral BCED. (2 Mark)
ar (ΔABC) = 36 cm2. Find the area of quadrilateral BCED. (2 Mark)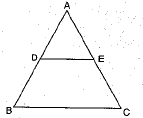
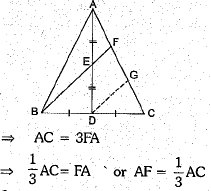
In a ΔABC, D is the mid-point of BC and E is the midpoint of AD. If BE produced meets AC in F, then prove that AF 1/3 AC.
Ans. 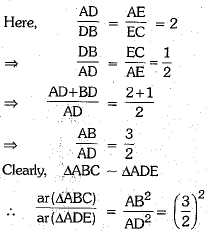
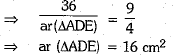
Now, ar (quad. BCED)
= ar(ΔABC)- ar (ΔADE) 36 -16 = 20 cm2
Or
Through D, draw DG || BF intersecting AC in G.
In ΔCBF, D is the mid-point of BC and DG || BF
⇒ G is the mid-point of CF
i.e., CG - GF ...(i)
Again, in ΔADG, E is the mid-point of AD and EF is parallel to DG
⇒ F is the mid-point of AG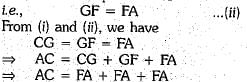
Q.24. In Fig., AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB - 60°. Find the length of chord AB. (2 Mark)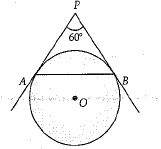
Ans. PA = PB
or, ∠PAB =∠PBA = 60°
∴ ΔPAB is an equilateral triangle.
Hence, AB - PA - 5 cm.
Q.25. A card is drawn at random from a pack o f 52 playing cards. Find the probability of drawing a card which is neither a spade nor a king. (2 Mark)
Ans. A pack of cards contains 52 cards.
∴ Total number of possible outcomes in the sample space = 52
Number of spade cards =13 and number of king cards other than spade = 3
∴ Total number of cards which are neither a spade nor a king = 52 - (13 + 3) = 3
Probability of drawing a card which is neither a spade nor a king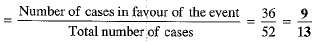
Q.26. Calculate the mode for the following frequency distribution (2 Mark)
Ans. As the class 40-50 has maximum frequency, so it is the modal class.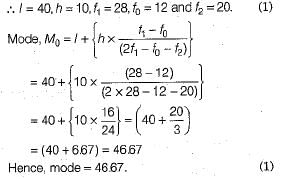
Section C
Q.27. Prove that (3+2√5) is an irrational number, given that √5 is an irrational number. (3 Mark)
Ans. Suppose 3+2√5 is a rational number. Then there exists co-prime integers a and b such that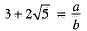
⇒ 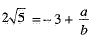
⇒ 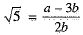
⇒ 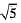 is a rational number,
is a rational number,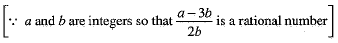
This contradicts the given fact that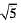 is an irrational number. So, our supposition is wrong.
is an irrational number. So, our supposition is wrong.
Hence, 3+2 √5 is an irrational number.
Q.28. Read the following passage and answer the question that follows:
A mathematics teacher Ramnivas Mathuriya organised a workshop for Class Xth students in the school auditorium to investigate the practice of students about subject knowledge. In order he write a polynomial x4 - 6x3 +16x2 - 25x + 10 on blackboard. After that he said the students, if we divide above polynomial by x2 - 2x + k, then the remainder comes out to be in the form of x + a, then find the value of k. (3 Mark)
Ans. By using long division method,
divide x4- 6x3 + 16x2 - 25x + 10
by x2 - 2x + k, we get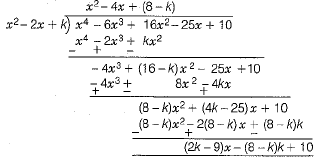
Here, remainder = (2k - 9)x - (8 - k)k +10
But the remainder is given in the form of x+ a,
∴ (2k - 9)x - (8 - k)k +10 = x + a
On comparing the coefficients of x and constant term both sides, we get
2k - 9 = 1 and - (8 - k)k + 10 = a
⇒ 2k = 10 and a = - (8 - k) k + 10
⇒ k = 5 and a = - 3x5 + 10
= -15 + 10 = -5
∴ k = 5 and a = - 5
Q.29. Solve the following pair of equations by reducing them to a pair of linear equations: (3 Mark)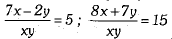
Or
In a competitive examination, one mark is awarded for each correct answer while 1/2 mark is deducted for every wrong answer 120 questions and got 90 marks. How many questions did she answer correctly ?
Ans. Given equations are, 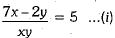
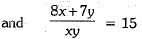 ...(ii)
...(ii)
Equations (i) and (ii) can be rewritten as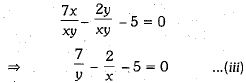
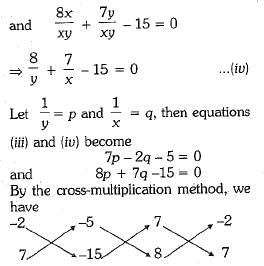
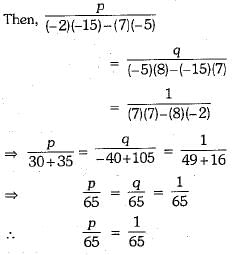
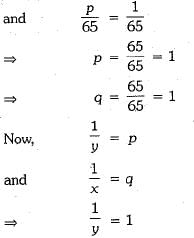
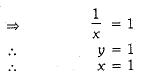
Hence, the required solution is x = 1 and y =1.
Or
Let x and y be the number of correct answers and wrong answers.
According to the statement of the question, we have
x + y = 120 ...(i)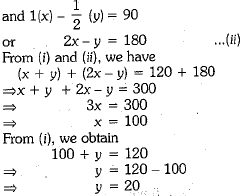
Hence, total number of questions correctly answered by Jayanti are 100.
Q.30. AB is a chord of circle with centre O. At B, a tangent PB is drawn such that its length is 24 cm. The distance of P from the centre is 26 cm. If the chord AB is 16 cm, find its distance from the centre. (3 Mark)
Ans. Given, AB is a chord of circle with centre 0 and tangent PB = 24cm, OP = 26cm.
Construction: Join O to B and draw OC ⊥ AB. By Pythagoras theorem,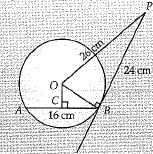
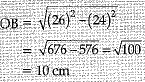
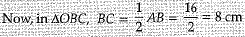
(Perpendicular drawn from the centre to a chord bisects it.)
OB = 10 cm
OC2 = OB2 - BC2
=102 - 82
OC2 = 36
OC = 6 cm
∴ Distance of the chord from the centre = 6 cm.
Or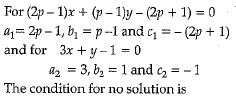
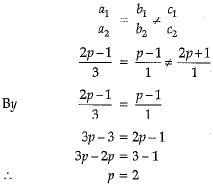
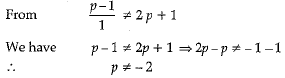
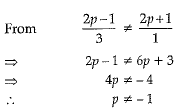
Hence, System has no solution when P = 2.
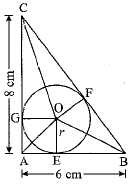
Q.31. ABC is a right-angled triangle right angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the circle. (3 Mark)
Ans. Using Pythagoras theorem in ABAC, we have
BC2 =AB2 + AC2
⇒ BC2 = 62 + 82 = 100
⇒ BC = 10 cm
Let O be the centre of the circle. The circle touches sides AB, BC and CA at E, F and G respectively. As tangent at any point of a circle is perpendicular to the radius through the point.
∴ OE ⊥ AB, OF ⊥ BC, OG ⊥ CA
Join O to A, B and C.
Now,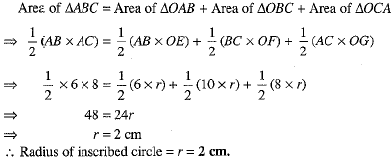
Q.32. Prove that (3 Mark)
(1 + cot A + tan A)(sin A - cos A)
sec3 A - cosec3 A
= sin2 A • cos2 A
Ans.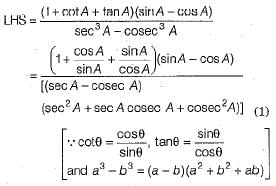
Q.33. In the given figure, three seniicirc/es A, B and C hawing diameter 3 cm each, another semicircle E hawing diameter 9 cm and a circle D of diameter 4 .5 cm.
Find the area of the shaded region. [Use π = 3.14] (3 Mark)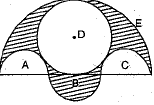
Ans. For semicircles A, B and C, we have diameter — 3 cm, radius = 1.5 cm
Area of semicircle A = 1/2π(1.5)2 cm2
Area of semicircle B = 1/2π(1.5)2 cm2
Area of semicircle C = 1/2π(1.5)2 cm2
For circle D, we have
diameter = 4.5 cm ⇒ radius = 4.5/2 cm
Area of circle D = 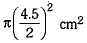
For semicircle E, we have
diameter = 9 cm ⇒ radius = 4.5 cm
Area of semicircle E = 1/2π(4.5)2 cm2
Now, Area of shaded region
= area of E + area of B - area of A - area of C - area of D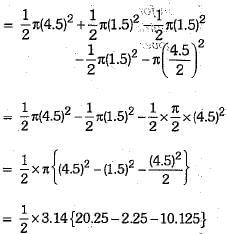
= 1.57 {7.875}
= 12.36375 cm2
Q.34. Prove that √2 is an irrational number. (3 Mark)
Ans. Let √2 be a rational number.
∴ 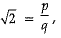
where p and q are co-prime integers and q ≠ 0
On squaring both the sides, we get,
Or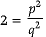
Or p2=2q2
∴ p2 is divisible by 2
∴ p is divisible by 2. ...(i)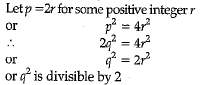
∴ q is divisible by 2 ...(ii)
From (i) and (ii), p and q are divisible by 2, which contradicts the fact that p and q are co-primes. Hence, our assumption is false.
∴ √2 is an irrational number.
Section D
Q.35. Solve for x : (4 Mark)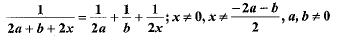
Ans. The given equation is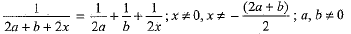
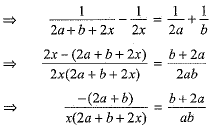
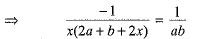 [On dividing by (b + 2a)]
[On dividing by (b + 2a)]
Cross-multiplying, we get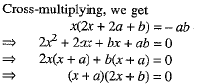
⇒ x + a =0 or 2x + b = 0
⇒ x= - a or x = - b/2
Hence, the roots of the equation be - a and -b/2.
Or
The sum of the areas of two squares is 640 m . If the difference o f their perim eters is 64 m, find the sides of the square.
Ans. Let the sides of two squares be x m and y m such that x > y.
sides of two squares be x m and y m such that x > y.
Sum of their areas =(x2 + y2) m2
and the difference of their perimeters = (4x - 4y) m
According to the given condition, we have
x2 + y2 = 640 ...(1)
and 4x - 4y = 64
⇒ x - y = 16 ...(2)
From (2), we get
y = x - 16 ...(3)
Putting the value of y from (3) in (1), we get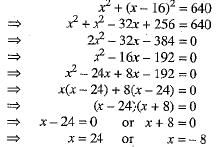
⇒ x = 24 [∴ Side (x) cannot be negative]
From (3), we get y = x - 16 = 24 - 16 = 8.
Hence, the sides of two squares are 24 m and 8 m.
Q.36. Find the length of the median drawn through A on BC of a ΔABC, whose vertices are A(7,-3), B(5,3) and C(3,-1) and also find the distance of the point A(7,-3) from the origin.
Or
Find The centre of a circle passing through the points (6,-6), (3,-7) and (3,3). (4 Mark)
Ans. The median from a vertex of a triangle bisects the opposite side, to that vertex. So, let AD be the median through A, then D be the mid-point of the side BC.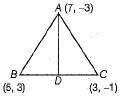
Now, coordinates of D = 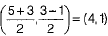
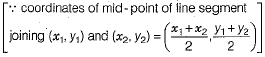
and length of median AD is given by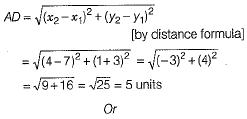
Let C (x, y) be the centre of the circle passing through the points P(6,-6), Q(3,-7) and R(3,3)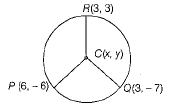
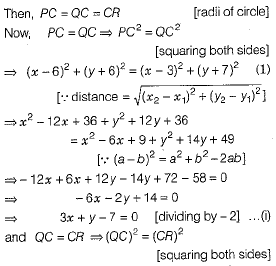
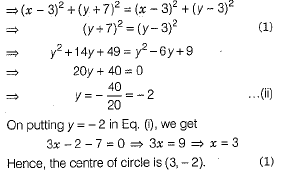
Q. 37. Solve the following equation f or x : 9x2- 9(a+ b)x + 2a2 + 5ab + 2b2 = 0
Or
Two water.taps together can fill a tank in 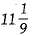 hours. The tap of smaller diameter takes 5 hours more than the larger one to fill the tank separately. Find the time in which each tap can separately fill the tank. (4 Mark)
hours. The tap of smaller diameter takes 5 hours more than the larger one to fill the tank separately. Find the time in which each tap can separately fill the tank. (4 Mark)
Ans. Given quadratic equation is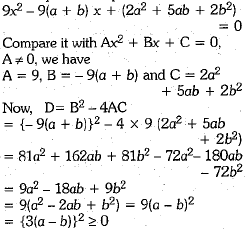
Real and unequal roots.
By using quadratic formula, we have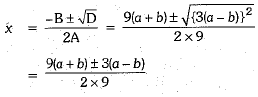
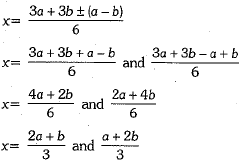
Hence, roots of the given quadratic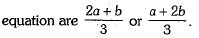
Time taken by two taps together to fill the tank 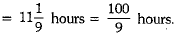
Let V be the volume of tank and x the number of hours required by the larger tap to fill the tank.
∴ Number of hours required by the smaller tap to fill the tank = (x + 5)
∴ Portion of the tank filled by larger tap in 1 hour = v/x
Portion of the tank filled by smaller tap in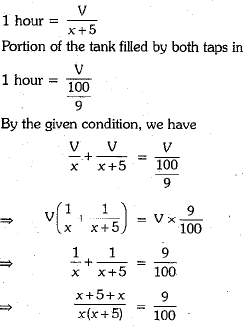
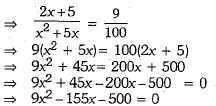
Now, we have a = 9, b = -155, c = - 500 By using quadratic formula, we obtain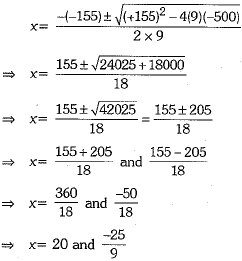
But -25/9 is not possible because time cannot be negative.
Hence, time required by the larger tap is x = 20 hours and time required by the smaller tap is
x + 5 = 20 + 5 = 25 hours.
Q.38. a, b and c are the sides of a right triangle, where c is the hypotenuse. A circle, of radius r, touches the sides of the triangle. Prove that r = 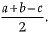 Construct a triangle ABC with BC = 7 cm, ∠ B = 60° and AB = 6 cm. Construct another triangle whose sides are (3/4) times of the corresponding sides of ΔABC. (4 Mark)
Construct a triangle ABC with BC = 7 cm, ∠ B = 60° and AB = 6 cm. Construct another triangle whose sides are (3/4) times of the corresponding sides of ΔABC. (4 Mark)
Ans. 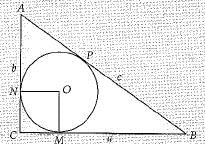
Let circle touches CB at M, CA at N and AB at P.
Now OM ⊥ CB and ON ⊥ AC (radius ⊥ tangent)
OM = ON (radii)
CM = CN (Tangents)
∴ OMCN is a square.
Let OM = r = CM = CN
AN = AP, CN = CM and BM = BP (tangent from external point)
AN = AP
⇒ AC -CN = AB-BP
b-r = c-BM
b-r = c-(a-r)
b-r = c-a+r
2r - a+b-c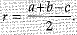
Or
Steps of construction:
1. Draw a line segment BC = 7 cm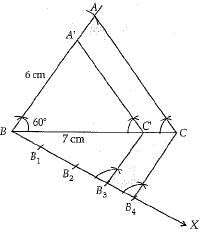
2. At point B draw a line BY making an angle of 60°.
3. With centre B mark an arc A of length 6 cm.
4. Join CA,
5. Draw a ray BX making an acute angle with BC.
6. Locate four points B1, B2, B3 and B4 on the line segment BX at equal distance.
7. Join B4C. Draw a parallel line through B3 to B4C intersecting line segment BC at C.
8. Through C' draw a line parallel to AC intersecting line segment AB at A'.
Hence ΔA'BC' is the required triangle.
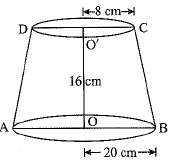
Q.39. A container opened at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container, at the rate of Rs 50 per litre. Also find the cost of metal sheet used to make the container, if it costs Rs 10 per 100 cm2. [Take n = 3.14] (4 Mark)
Ans. Let r and R be radii of the lower and upper end of the container in the form of a frustum of a cone and h, / be its height and slant height respectively.
Radius of the lower end, r - 8 cm; radius of the upper end, R - 20 cm and height of the container, h - 16 cm.
Let V be the volume of the container. Then
Volume of the container = 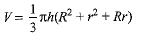
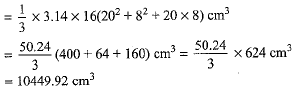
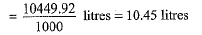
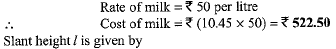
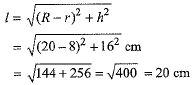
Let S be the surface area of the metal sheet used to make the container. Surface area of the metal sheet used to make the container is given by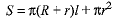
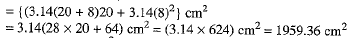
Cost of metal sheet = Rs 10 per 100 cm2 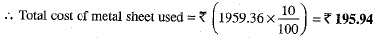
Q.40. The following table gives the height of trees
Draw 'less than ogive' and ‘more than ogive'. Also, find the median.
Or
The mean of the following table is 50. The frequencies f1 and f2 in class 20-40 and 60-80 are missing. Find the missing frequencies. (4 Mark)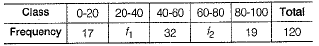
Ans. Given distribution is cumulative frequency distribution of less than type.
Now, we mark the upper limits along X-axis and cumulative frequencies along Y-axis, on the graph paper. Then, plot the points (7,26), (14, 57), (21,92), (28, 134), (35, 216), (42, 287), (49, 341) and (56, 360). Join all these points by a freehand smooth curve to obtain an ogive of less than type,
Now, let us form the cumulative frequency distribution of more than type, as shown below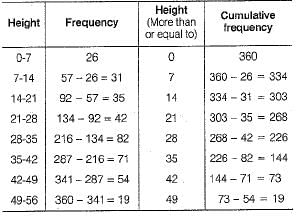
Now, we plot the points (0, 360), (7, 334), (14, 303), (21,268), (28, 226), (35,144), (42,73) and (49,19) on the same graph paper by choosing a suitable scale. Join all these points by a freehand smooth curve to obtain an ogive of more than type,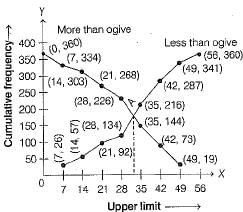
The two ogives intersect at point A. Now, we draw a perpendicular line from A to the X-axis, the intersection point on X-axis is 31.9. Thus, the required median is 31.9
or
Let us assumed mean be A = 50 and h = 20.
Table for step deviation is given below
We have, 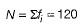 [given]
[given]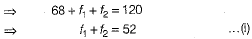
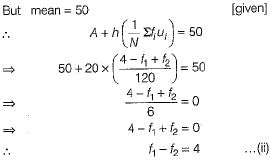
On solving Eqs. (i) and (ii), we get
f1 = 28 and f2 = 24
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Mathematics: CBSE Sample Question Paper (2019-20) - 4 - Mathematics (Maths) Class 10
| 1. What are the key topics covered in the Class 10 Mathematics CBSE Sample Question Paper for 2019-20? |  |
| 2. How can I effectively use the CBSE Sample Question Paper to prepare for my Class 10 Mathematics exam? |  |
| 3. Are the questions in the CBSE Sample Question Paper representative of the actual Class 10 Mathematics exam? |  |
| 4. What is the marking scheme for the Class 10 Mathematics exam according to the CBSE Sample Question Paper? |  |
| 5. Where can I find additional resources to help with my Class 10 Mathematics preparation alongside the CBSE Sample Question Paper? |  |
















