Class 10 Maths Chapter 14 Previous Year Questions - Probability
Previous Year Questions 2025
Q1: If in a lottery, there are 10 prizes and 30 blanks, then the probability of winning a prize is:
(a) 1/4
(b) 1/3
(c) 3/4
(d) 2/3
 View Answer
View Answer 
Ans: (a)
Given, number of prizes = 10
Number of blanks = 30
Total outcomes= 10 + 30 = 40
∴ Probability of wining a prize = 10/40 = 1/4
Q2: A die is thrown once. The probability of getting a number which is not a factor of 36, is:
(a) 1/2
(b) 2/3
(c) 1/6
(d) 5/6
 View Answer
View Answer 
Ans: (c)
When a die is thrown, possible outcomes are 1, 2, 3, 4, 5 and 6. Out of them factors of 36 are 1, 2, 3, 4 and 6.
Let E be the event 'getting a number not a factor of 36.
∴ E = {5}
∴ P(E) = 1/6
Q3: A card is selected at random from a deck of 52 playing cards. The probability of it being a red face card is:
(a) 3/13
(b) 2/13
(c) 1/2
(d) 3/26
 View Answer
View Answer 
Ans: (d)
Total number of cards= 52
Number of red face cards = 6
∴ P(Red face card) = 6/52 = 3/26
Q4: Assertion (A): The probability of selecting a number at random from the numbers 1 to 20 is 1.
Reason (R) : For any event E, if P(E) = 1, then E is called a sure event.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
(c) Assertion (A) is true, but Reason (R) is false.
(d) Assertion (A) is false, but Reason (R) is true.
 View Answer
View Answer 
Ans: (d)
The probability of selecting a number at random from the numbers 1 to 20 is 1/20.
So, Assertion is false.
For, P(E) = 1, E is called a sure event.
So, Reason is true.
Hence, Assertion is false, but Reason is true.
Q5: Two coins are tossed simultaneously. The probability of getting at least one head is
(a) 1/4
(b) 1/2
(c) 3/4
(d) 1
 View Answer
View Answer 
Ans: (c)
Total outcomes on tossing two coins = {(H, H), {H, T), (T, H), (T, T)}
Favourable outcomes= {{H, H), {H, T), (T, H)} 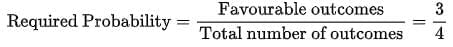
Q6: In an experiment of throwing a die,
Assertion (A): Event E1: getting a number less than 3 and Event E2 : getting a number greater than 3 are complementary events.
Reason (R): If two events E and Fare complementary events, then P(E) + P(F) = 1.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
(c) Assertion (A) is true, but Reason (R) is false.
(d) Assertion (A) is false, but Reason (R) Q is true.
 View Answer
View Answer 
Ans: (d)
Clearly, reason is true.
On throwing a die, favourable outcomes are {1, 2, 3, 4, 5, 6}. 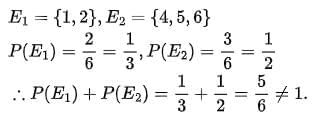
∴ E1 and E2 are not complementary events.
∴ Assertion is false.
Q7: The probability of guessing the correct answer of a certain test question is x/12. If the probability of not guessing the correct answer is 5/6, then find the value of x.
 View Answer
View Answer 
Ans: Let A be the event of guessing the correct answer and A' be the event of not guessing the correct answer.
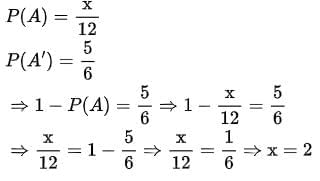
Q8: The number of red balls in a bag is three more than the number of black balls. If the probability of drawing a red ball at random from the given bag is 12/23, find the total number of balls in the given bag.
 View Answer
View Answer 
Ans:
Let the number of black balls be x.
⇒ Number of red balls= x + 3
∴ Total balls = x + x + 3 = 2x + 3
Now, probability of drawing a red ball at random = 12/23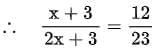
⇒ 23x + 69 = 24x + 36
⇒ 24x - 23x = 69 - 36
⇒ x = 33
∴ Total Balls= 2 * 33 + 3 = 69
Q9: If 65% of the population has black eyes, 25% have brown eyes and the remaining have blue eyes, what is the probability that a person selected at random has:
(a) blue eyes?
(b) brown or black eyes?
 View Answer
View Answer 
Ans: Probability that a person has black eyes = 65/100
Probability that a person has brown eyes = 25/100
(a) Probability that person selected has blue eyes =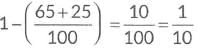
(b) Probability that person selected has brown or black eyes =
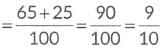
Q10: All face cards of spades are removed from a pack of 52 playing cards and the remaining pack is shuffled well. A card is then drawn at random from the remaining pack. Find the probability of getting:
(a) a face card
(b) an ace or a jack
 View Answer
View Answer 
Ans:
Total number of cards in a deck = 52
Number of face cards of spades in a deck = 3
Number of cards left in the deck = 52 - 3 = 49
(a) Total number of face cards left in the deck = 12 - 3 = 9
Probability that the card drawn is a face card= 9/49
(b) Number of a ace and jack cards left in the deck = 4 + 3 = 7
Probability that the card drawn is an ace or a jack = 7/49 = 1/7
Q11: Three unbiased coins are tossed simultaneously. Find the probability of getting:
(a) exactly two tails
(b) at least one head
(c) at most two heads
 View Answer
View Answer 
Ans: Possible outcomes are: {HHH, HHT, HTT, THT, HTH, TTT, TTH, THH}
∴ Total number of possible outcomes= 8
(a) Favourable outcomes are {HTT, THT, TTH} i.e., 3 in number
∴ P(exactly two tails) = 3/8
(b) Favourable outcomes are {HTH, HHT, HTT, THT, HTH, TTH, THH} i.e., 7 in number
∴ P(at least one head) = 7/8
(c) Favourable outcomes are {HHT, HTT, THT, TTT, HTH, TTH, THH} i.e., 7 in number
∴ P(at most two heads) = 7/8
Q12: Two dice are rolled together. Find the probability of getting:
(i) a multiple of 2 on one and a multiple of 3 on the other die.
(ii) the product of two numbers on the top of the two dice is a perfect square number.
 View Answer
View Answer 
Ans:
Total number of possible outcomes= 6 x 6 = 36
(i) Favourable outcomes are (2, 3), (2, 6), (3, 2), (3, 6), (4, 3), (4, 6), (6, 2), (6, 3), (6, 4), (6, 6).
∴ Probability of getting a multiple of 2 on one and a multiple of 3 on the other die = 10/36 = 5/18
(ii) Favourable outcomes are (1, 1), (2,2), (3,3), (4,4), (5, 5), (6, 6), (1, 4), (4, 1). ·
Probability of getting the product of two numbers on the top of the two dice is a perfect square number = 8/36 = 2/9
Q13: Two dice are thrown at the same time. Determine the probability that the difference of the numbers on the two dice is 2.
 View Answer
View Answer 
Ans: When two dice are thrown at same time, total number of outcomes = 6 x 6 = 36
Possible outcomes when difference of numbers on two dice is 2
= {(1, 3), (2, 4), (3, 1), (3, 5), (4, 2), (4, 6), (5, 3), (6, 4)}
Number of favourable outcomes= 8 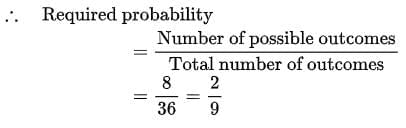
Q14: A bag contains some red and blue balls. Ten percent of the red balls, when added twenty percent of the blue balls, give a total of 24. If three times the number of red balls exceeds the number of blue balls by 20, find the number of red and blue balls.
 View Answer
View Answer 
Ans: Let the number of red balls= x
and number of blue balls= y
According to question,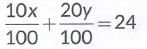
⇒ x + 2y = 240 ... (i)
Also, 3x - y = 20 ... (ii)
Multiply eqn (ii) by 2, then adding to eqn (i), we get
6x - 2y + x + 2y = 40 + 240
⇒ 7x = 280 ⇒ x = 40
Put the value of x in eqn. (i),
40 + 2y= 240
⇒ 2y = 200 ⇒ y = 100
Therefore, number of red balls is 40 and number of blue balls is 100.
Previous Year Questions 2024
Q1: A bag contains 3 red balls, 5 white balls and 7 black balls. The probability that a ball drawn from the bag at random will be neither red nor black is: (1 Mark) (CBSE 2024)(a) 1/3
(b) 1/5
(c) 7/15
(d) 8/15
 View Answer
View Answer 
Ans: (a)
No. of red balls = 3
No. of white balls = 5
No. of black balls = 7
Total balls = 15
Probability that ball drawn is neither red nor black = 5/15 = 1/3
Q2: The probability of getting a bad egg in a lot of 400 eggs is 0.045. The number of good eggs in the lot is: (1 Mark) (CBSE 2024)
(a) 18
(b) 180
(c) 382
(d) 220
 View Answer
View Answer 
Ans: (c)
Probability of getting bad in the lot = 0.045
Let the no. of bad eggs = x
∴ Probability of bag eggs
= No. of bad eggsTotal eggs
⇒ 0.045 = x/400
⇒ x = 400 × 0.045
⇒ x = 18
No. of bad eggs = 18
No. of good eggs = 400 – 18
= 382
Q3: Two dice are thrown together. The probability that they show different numbers is: (1 Mark) (CBSE 2024)
(a) 1/6
(b) 5/6
(c) 1/3
(d) 2/3
 View Answer
View Answer 
Ans: (b)
Total outcomes, when two dice are thrown
= {(1, 1)(1, 2)(1, 3)(1, 4)(1, 5)(1, 6)
(2, 1)(2, 2)(2, 3)(2, 4)(2, 5)(2, 6)
(3, 1)(3, 2)(3, 3)(3, 4)(3, 5)(3, 6)
(4, 1)(4, 2)(4, 3)(4, 4)(4, 5)(4, 6)
(5, 1)(5, 2)(5, 3)(5, 4)(5, 5)(5, 6)
(6, 1)(6, 2)(6, 3)(6, 4)(6, 5)(6, 6)}
Outcomes of showing same numbers = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
No. of favourable outcomes = 36 - 6 = 30
Total outcomes = 36
So, P(E) = 30/36
= 5/6
Q4: Assertion (A): In a cricket match, a batsman hits a boundary 9 times out of 45 balls he plays. The probability that in a given ball, he does not hit the boundary is 4/5.
Reason (R): P(E) + P(not E) = 1. (1 Mark) (CBSE 2024)
(a) Both assertion (A) and reason (R) are true, and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true, but reason (R) is not the correct explanation of assertion (A).
(c) The assertion (A) is true, but the reason (R) is false.
(d) The assertion (A) is false, but the reason (R) is true.
 View Answer
View Answer 
Ans: (a) Assertion:
Total balls (outcomes) = 45
No. of times boundaries hit = 9
(E = hitting the boundary) = 9/45
= 1/5
∴ P(E= not hitting the boundary)
= 1 - 15 = 45
Reason: This is a fundamental property of probability:
The sum of the probability of an event P(E) and the probability of its complement P(not E) is always equal to 1.
Thus, Reason (R) is also true.
Previous Year Questions 2023
Q5: In a group of 20 people. 5 can't swim. If one person is selected at random, then the probability that he/she can swim is (1 Mark) (2023)
(a) 3/4
(b) 1/3
(c) 1
(d) 1/4
 View Answer
View Answer 
Ans: (a)
Total number of people = 20
Number of people who can't swim = 5
Number of people who can swim = 20 - 5 = 15
∴ Required probability = 15/20 = 3/4
Q6: The probability of the occurrence of an event is denoted by p, and the probability of the non-occurrence of the event is denoted by q. The relation between p and q is (1 Mark) (2023)
(a) p + q = 1
(b) p = 1, q = l
(c) p = q - 1
(d) p + p + 1 = 0
 View Answer
View Answer 
Ans: (a)
Probability of happening of an event + Probability of non - happening of an event
∴ p +q = 1
Q7: A girl calculates that the probability of her winning the first prize in a lottery is 0.08. If 6000 tickets are sold, how many tickets has she bought? (1 Mark) (2023)
(a) 40
(b) 240
(c) 480
(d) 750
 View Answer
View Answer 
Ans: (c)
Probability of winning first prize = Ticket bought by girl / Total ticket sold
⇒ 0.08 = Ticket bought by girl / 6000
⇒ Ticket bought by girl = 0.08 x 6000 = 480
Q8: Two dice are thrown together. The probability of getting the difference of numbers on their upper faces equals 3 is
(1 Mark) (CBSE, 2023)
(a) 1/9
(b) 2/9
(c) 1/6
(d) 1/12
 View Answer
View Answer 
Ans: (c)
Total number of outcomes = 6 x 6 = 36
Favourable outcomes are {(1,4), (2, 5), (3, 6), (4, 1), |5. 2), (6.3)} i.e., 6 in number
∴ Required probability = 6/36 = 1/6
Q9: A card is drawn at random from a well-shuffled pack of 52 cards. The probability that the card drawn is not an ace is (1 Mark) (2023)
(a) 1/13
(b) 9/13
(c) 4/13
(d) 12/13
 View Answer
View Answer 
Ans: (d)
Total number of cards = 52
Number of ace card =4
∴ Number of non ace card = 52 - 4 = 48
∴ Required probability = 48/52 = 12/13
Q10: DIRECTIONS: In the question, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option out of the following: (1 Mark) (CBSE 2023)
Assertion (A): The probability that a leap year has 53 Sundays is 2/7.
Reason (R): The probability that a non-leap year has 53 Sundays is 5/7.
(a) Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true, and Reason (R) is not the correct explanation of Assertion (A).
(c) The assertion (A) is true, but the Reason (R) is false.
(d) The assertion (A) is false, but the Reason (R) is true.
 View Answer
View Answer 
Ans: (c)
The leap year has 366 days, i.e, 52 weeks and 2 days.
∴ Required probability = 2/7
The non-leap year has 365 days. i.e.. 52 weeks and 1 day.
∴ Required probability = 1/7
Therefore, assertion is true but reason is false.
Q11: A bag contains 5 red balls and n green balls. If the probability of drawing a green ball is three times that of a red ball, then the value of n is (1 Mark) (2023)
(a) 18
(b) 15
(c) 10
(d) 20
 View Answer
View Answer 
Ans: (b)
Probability of drawing a green ball = 3 x Probability of drawing a red ball
n5 + n = 3 × 55 + n
Since 5+n is common and non-zero, we can cancel it.
n = 3×5
Q12: A bag contains 4 red, 3 blue and 2 yellow balls. One ball is drawn at random from the bag. Find the probability that the drawn ball is (i) red and (ii) yellow. (2 Marks) (2023)
 View Answer
View Answer 
Ans: Number of red balls =4
Number of blue balls = 3
Number of yellow balls = 2
Total number of balls = 4 + 3 + 2= 9
(i) P(drawing a red balI) = 4/9
(ii) P(drawing a yellow ball) = 2/9
Q13: If a fair coin is tossed twice, find the probability of getting 'almost one head. ' (2 Marks) (CBSE 2023)
 View Answer
View Answer 
Ans: Let A be the event of getting atmost one head, and S be the sample space.
S = (HH, HT, TH, TT) and A = (HT, TH, TT)
⇒ n(S) = 4
Also, n(A) = 3
Required probability = n(A) / n(S)
= 3/4
Previous Year Questions 2022
Q14: The probability of getting two heads when two fair coins are tossed together is (2022)
(a) 1/3
(b) 1/4
(c) 1/2
(d) 1
 View Answer
View Answer 
Ans: (b)
Sample space = {(H,H), (H,T), (T,H), (T,T)}
∴ Number of total outcomes = 4
Favourable outcomes = {(H,H)}
∴ Number of favourable outcomes = 1
∴ Required probability = 1/4
Q15: In a single throw of a die. The probability of getting a composite number is (2022)
(a) 1/3
(b) 1/2
(c) 2/3
(d) 5/6
 View Answer
View Answer 
Ans: (a)
Sample space = (1, 2, 3, 4, 5, 6)
∴ Number of total outcomes = 6
Favourable outcomes = (4, 6)
∴ Number of favourable outcomes = 2
∴ Required probability = 2/6 = 1/3
Q16: The probability that a non-leap year has 53 Wednesdays is (2022)
(a) 1/7
(b) 2/7
(c) 5/7
(d) 6/7
 View Answer
View Answer 
Ans: (a)
We know that there are 52 complete weeks = 364 days
Since, it is non leap year.
So. there will be 52 Wednesdays and remaining 365th day may be any of the days of week
So, total number of ways = 7
∴ Number of favourable outcomes = 1
∴ Required probability = 1/7
Q17: From the letters of the word "MANGO", a letter is selected at random. The probability that the letter is a vowel is (2022)
(a) 1/5
(b) 3/5
(c) 2/5
(d) 4/5
 View Answer
View Answer 
Ans: (c)
Total number of letters in the word MANGO are 5.
So, number of total outcomes = 5
Vowels in the word ‘MANGO’ are A, O
So, number of favourable outcomes = 2
∴ Required probability = 2/5
Previous Year Questions 2021
Q18: Case study-based questions are compulsory. Attempt any 4 sub-parts from the question. Each sub-part carries 1 mark. (2021)During summer break, Harish wanted to play with his friends, but it was too hot outside, so he decided to play some indoor games with his friends. He collects 20 identical cards and writes the numbers 1 to 20 on them (one number on one card). He puts them in a box. He and his friends make a bet on the chances of drawing various cards out of the box. Each was given a chance to tell the probability of picking one card out of the box.
Based on the above, answer the following questions:
(i) The probability that the number on the card drawn is an odd prime number is
(a) 3/5
(b) 2/5
(c) 9/20
(d) 7/20
 View Answer
View Answer 
Ans: (d)
Card numbered from {1,2, 3, ...., 20}
Total number of possible outcomes = 20
Odd prime numbers from 1 to 20 = {3, 5, 7, 11,13,17,19)
Total number of favourable outcomes = 7
Hence, the probability that the number on the card drawn is an odd prime number = 7/20
(ii) The probability that the number on the card drawn is a composite number is
(a) 11/20
(b) 3/5
(c) 4/5
(d) 1/2 [2021, 1 Mark]
 View Answer
View Answer 
Ans: (a)
Total number of composite numbers between 1 to 20 = [4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20)
Total number of favourable outcomes = 11
So, the probability that the number on the drawn card is a composite number = 11/20
∴ Required Probability = 11/20
(iii) The probability that the number on the card drawn is a multiple of 3, 6 and 9 Is
(a) 1/20
(b) 1/10
(c) 3/20
(d) 0
 View Answer
View Answer 
Ans: (c)
Multiple of 3 = {3, 6, 9,12,15, 18}
Multiple of 6 = (6, 12, 18)
Multiple of 9 = (9, 18)
Total number of favourable outcomes = 1
Hence the probability that the card is a multiple of 3, 6 and 9 = 1/20
∴ Required Probability = 1/20
(iv) The probability that the number on the card drawn is a multiple of 3 and 7 is
(a) 3/10
(b) 1/10
(c) 0
(d) 2/5 [2021, 1 Mark]
 View Answer
View Answer 
Ans: (c)
Multiple of 3 between 1 to 20 = {3, 6, 9, 12,15, 18}
Multiple of 7 between 1 to 20 = (7,14)
∴ Multiple of 3 and 7 = 0
∴ Total number of favourable outcomes = 0/20
∴ Required Probability = 0
(v) If all cards having odd numbers written on them are removed from the lie box and then one card is drawn from the remaining cards, the probability of getting a card having a prime number is
(a) 1/20
(b) 1/10
(c) 0
(d) 1/5
 View Answer
View Answer 
Ans: (b)
If all odd number cards are removed then remaining cards which are left = {2,4, 6, 8,10,12,14,16, 18, 20}
Now, prime number cards in remaining cards = 1
So, the probability of getting a prime number from the remaining cards = 1/10
Previous Year Questions 2020
Q19: The probability of an event that is sure to happen is _______. (2020)
 View Answer
View Answer 
Ans: The probability of an event that is sure to happen is 1.
Q20: If the probability of an event E happening is 0.023, then P(E) = ________. (2020)
 View Answer
View Answer 
Ans: Given, P(E) =0.023
P(E) = 1- P(E) = 1 - 0.023 = 0.977
Q21: A letter of the English alphabet Is chosen at random. What Is the probability that the letter is a consonant? (CBSE 2020)
 View Answer
View Answer 
Ans: Total number of English alphabets = 26
Number of consonants = 26 - 5 = 21
∴ Number of favourable outcomes = 21
P (chosen letter is a consonant) = 21/26
Q22: A die is thrown once. What is the probability of getting a number less than 3? (2020)
 View Answer
View Answer 
Ans: Total number of outcomes = 6
Favourable outcomes are {1.2} i.e.. 2 in number
∴ Required probability = 2/6 = 1/3
Q23: If the probability of winning a game is 0.07, what is the probability of losing it? (2020)
 View Answer
View Answer 
Ans: Given, probability of winning a game is 0.07
∴ Probability of losing it = 1 - 0.07 = 0.93
Q24: A jar contains 18 marbles. Some are red, and others are yellow. If a marble is drawn at random from the jar. The probability that it is red is 2/3. Find the number of yellow marbles in the jar. (2020)
 View Answer
View Answer 
Ans: There a re 18 marbles in the jar.
∴ Number of possible outcomes = 18
Let there are x yellow marbles in the jar.
∴ Number of red marbles = 18 - x
⇒ Number of favourable outcomes = (18 - x)
∴ Probability of drawing a red marble = (18 - x) / 18
Now. according to the question, = (18 - x) / 18 = 2/3
⇒ 3(18 - x ) = 2 x 18
⇒ 54 -3x = 36
⇒ 3x = 18
⇒ x = 6
So, number of yellow marbles in jar = 6
Q25: A die is thrown twice. What is the probability that
(i) 5 will come up at least once, and
(ii) 5 will not come up either time? (2020)
 View Answer
View Answer 
Ans: Since, throwing a die twice or throwing two dice simultaneously are same.
Possible outcomes are:
{(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6),
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6),
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6),
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}
(i) Let N be the event that 5 will come up at least once, the number of favourable outcomes:
= 5 + 6
= 11
∴ P(N) = 1136
(ii) Let E be the event that 5 does not come up either time, then the number of favourable outcomes:
= [36 - (5 + 6)]
= 25
∴ P(E) = 2536
Q26: If a number x is chosen at random from the numbers -3, -2, -1, 0, 1, 2, 3. What is the probability that x2 ≤ 4? (2020)
 View Answer
View Answer 
Ans: Total number of outcomes = {-3, -2, -1,0, 1, 2, 3} i.e. 7.
∴ Number of favourable outcomes = (-2, 1, 0, 1, 2) i.e., 5.
∴ Required Probability = 5/7
Q27: Two dice are thrown simultaneously. What is the probability that the product of the numbers appearing on the top is 1? (CBSE 2020)
 View Answer
View Answer 
Ans: Total number of possible outcomes = 36
Only one outcome, i.e., (1, 1) has the product of the two numbers as 1.
So, the required probability is 1/ 36 .
Q28: A Group Housing Society has 600 members who have their houses on the campus and decided to hold a Tree Plantation Drive on the occasion of the New Year. Each household was given the choice of planting saplings of its choice. The number of different types of saplings planted were:
(1) Neem – 125
(2) Peepal - 165
(3) Creepers – 50
(4) Fruit plants – 150
(5) Flowering plants – 110
At the opening ceremony, one of the plants is selected randomly for a prize. After reading the above passage, answer the following questions.
What is the probability that the selected plant is:
(A) A fruit plant or a flowering plant?
(B) either a Neem plant or a Peepal plant? (CBSE 2020)
 View Answer
View Answer 
Ans: (A) Of the 600 plants, there are 150 fruit plants and 110 flowering plants.
So, required probability
= (150 + 110)600 = 260600 i.e., 1330
=(B) Of the 600 plants, there are 290 (125 + 165) plants which are either neem plants or peepal plants.
So, required probability = 290/600 i.e., 29/60
Q29: If a number x is chosen at random from the numbers –3, –2, –1, 0, 1, 2, 3. What is the probability that x2 < 4? (CBSE 2020)
 View Answer
View Answer 
Ans: All possible outcomes are –3, –2, –1, 0, 1, 2, 3
Favourable outcomes are – 1, 0, 1 (As x2 < 4)
So, required probability = 3/7
Q30: Find the probability that a leap year selected at random will contain 53 Sundays and 53 Mondays. (CBSE 2020)
 View Answer
View Answer 
Ans: A leap year has 52 complete weeks + 2 days.
These two days may be
(Sun, Mon), (Mon, Tue), (Tue, Wed), (Wed, Thu), (Thu, Fri), (Fri, Sat) and (Sat, Sun).
Of the 7 possible outcomes, only 1
i.e., (Sun, Mon) is the favourable outcome.
So, required probability is 1/7
Q31: A game in a booth at a Diwali fair involves using a spinner first. Then, if the spinner stops on an even number, the player is allowed to pick a marble from a bag. The spinner and the marbles in the bag are represented in the figure.
Prizes are given when a black marble is picked. Shweta plays the game once.

(A) What is the probability that she will be allowed to pick a marble from the bag?
(B) Suppose she is allowed to pick a marble from the bag; what is the probability of getting a prize, when it is given that the bag contains 20 marbles out of which 6 are black? (CBSE 2020)
 View Answer
View Answer 
Ans: (A) Shweta will be allowed to pick up a marble, only when the spinner stops on an even number.
P(getting an even number) = 5 / 6
Hence, the probability that she will be allowed to pick a marble from the bag is 5 / 6
(B) P (getting a black marble) = 6 / 20 , or 3 / 10 .
∴ Probability of getting a prize is 3 / 10 .
Previous Year Questions 2019
Q32: Cards numbered 7 to 40 were put in a box. Poonam selects a card at random. What is the probability that Poonam selects a card which is a multiple of 7? (2019) View Answer
View Answer 
Ans: Cards are numbered from 7 to 40. i.e. {7,8,9, ......, 40}
So, total number of outcomes = 34
Multiple of 7 lies between 7 to 40 are {7, 14, 21, 28, 35}
∴ Total number of favourable outcomes= 5
∴ Required probability = 5/34
Q33: A card is drawn at random from a pack of 52 playing cards. Find the probability of drawing a card that is neither a spade nor a king. (2019)
 View Answer
View Answer 
Ans: Total number of cards = 52
Total number of spade cards = 13
Total number of king cards = 4
Total number of spade cards and king cards = 13 + 4 - 1 = 16
[One card is subtracted as it is already included as a king of spade]
∴ Probability of drawing a spade or king card = 16/52
So, probability of drawing a card which is neither a spade nor a king = 1- 16/52
= 9/13
Q34: A pair of dice is thrown once. Find the probability of getting
(i) there is an even number on each dice
(ii) a total of 9. (2019)
 View Answer
View Answer 
Ans: If a pair of dice is thrown once, then possible outcomes are:
{(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6),
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6),
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6),
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}
∴ Number of possible outcomes are 36.
(i) Total possible outcomes of getting even number on each die
= {( 2, 2), ( 2, 4 ), ( 2, 6 ), ( 4, 4 ), (4, 6), (6, 6). (6, 2), (6, 4 ), (4, 2)}
Number of favourable outcomes = 9
∴ Required probability of getting an even number on each die = 9/36 = 1/4
(ii) Total possible outcomes of getting a total of 9
= {(3, 6), (4, 5), ( 5, 4), (6, 3)} which are 4 in number.
∴ Probability of getting a total of 9 = 4/36 = 1/9
Q35: A bag contains some balls, of which x are white, 2x are black, and 3x are red. A ball is selected at random. What is the probability that it is (2019)
(i) not red
(ii) white?
 View Answer
View Answer 
Ans: We have, total number of balls = x + 2x + 3x = 6x
Total number of outcomes =6x
(i) Number of favourable outcomes = 3x
∴ Probability of getting red ball = 3x /6x = 1/2
Now, probability of not getting red ball = 1-1/2 = 1/2
∴ Required probability = 1/2
(ii) Total number of favourable outcomes = x
∴ Probability of getting white ball = x / 6x
∴ Required probability = 1/6
Q36: A die is thrown once. Find the probability of getting a number which
(i) is a prime number
(ii) lies between 2 and 6. (2019)
 View Answer
View Answer 
Ans: Total possible outcomes are f 1, 2, 3, 4, 5, i.e., 6 in number.
(i) Favourable outcomes are {2, 3, 5} i.e.. 3 in number.
∴ P (getting a prime number) = 3/6 = 1/2
(ii) Favourable outcomes are {3, 4, 5} i.e., 3 in number.
∴ P(getting a number lying between 2 and 6) = 3/6 = 1/2
Q37: A game consists of tossing a coin 3 times and noting the outcome each time. If getting the same result in all the tosses is a success, find the probability of losing the game. (2019)
 View Answer
View Answer 
Ans: When a coin is tossed 3 times, then total possible outcomes are
{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
∴ Total number of possible outcomes = 8
Possible outcomes to lose the game are {HHT, HTH, THH, HTT,THT, TTH}
∴ Number of favourable outcomes = 6
∴ Required Probability = 6/8 = 3/4
Q38: Cards marked with numbers 5 to 50 (one number on one card) are placed in a box and mixed thoroughly. One card is drawn at random from the box. Find the probability that the number on the card taken out is
(i) a prime number less than 10,
(ii) a number which is a perfect square. (2019)
 View Answer
View Answer 
Ans: Total number of cards = 50 - 5 + 1 = 46
∴ Total number of possible outcomes = 46
(i) Prime numbers less than 10 are 5, 7.
So, number of favourable outcomes = 2
∴ P(getting a prime number less than 10) = 2/46 = 1/23
(ii) Perfect squares from 5 to 50 are 9, 16, 25, 36, 49 i.e., 5 in number.
∴ P (getting a number which is a perfect square) =5/46
Q39: A child has a die whose 6 faces show the letters given below: The die is thrown once: What is the probability of getting (i) A (ii) B? (2019)
The die is thrown once: What is the probability of getting (i) A (ii) B? (2019)
 View Answer
View Answer 
Ans: Total number of faces in a die = 6
(i) Number of favourable outcomes = 3
∴ P(getting A) = 3/6 = 1/2
(ii) Number of favourable outcomes = 2
∴ P (getting B) = 2/6 = 1/3
Previous Year Questions 2017
Q40: A number is selected at random from the natural numbers 1 to 20. Find the probability that the selected number is a prime number. (CBSE 2017) View Answer
View Answer 
Ans: Total number of outcomes = 20
Let, E be the event that a number selected is a prime number.
Since, the prime number between 1 to 20 (or favourable cases) are 2, 3, 5, 7, 11, 13, 17, 19
∴ Number of favourable outcomes = 8
∴ P(E) = Number of favourable outcomes / Total number of outcomes
= 8/20 = 2/5
Hence, the required probability is 2/5
Q41: A number is chosen at random from the numbers –3, –2, –1, 0, 1, 2, 3. What will be the probability that the square of this number is less than or equal to 1? (CBSE 2017)
 View Answer
View Answer 
Ans: The given numbers are {–3, –2, –1, 0, 1, 2, 3}
The square of these numbere are {9, 4, 1, 0, 1, 4, 9}
∴ Total numbers of outcomes = 7
The square of numbers that are less than or equal to 1 = {-1, 0, 1}
∴ Number of favourable outcomes = 3
P(getting a square of a number less than or equal to 1) = 3 / 7
Hence, the required probability is 3 / 7 .
Q42: A lot consists of 144 ball pens, of which 20 are defective. The customers will buy a ballpoint pen if it is good but will not buy a defective ballpoint pen. The shopkeeper draws one pen at random from the lot and gives it to a customer. What is the probability that
(A) customer will buy the ball pen?
(B) customer will not buy the ball pen? (CBSE 2017)
 View Answer
View Answer 
Ans: (A) Total number of ball pens = 144
∴Total number of outcomes is 144.
Also, the number of defective ball pens = 20
∴ Non-defective ball pens = 144 – 20 = 124 (A)
Let E1 be the event that customer will buy a ball pen i.e., ball pen is non-defective.
∵Total number of non-defective pens = 124
∴ P(E1) = 124144 = 3136
Hence, the probability that customer will buy the ball pen is 31 / 36 .
(B) Probability of not buying the ball pen
= 1 – Probability of buying the ball pen
= 1 – P(E1)
= 1 – 31 / 36
= 5 / 36
Hence, the probability that the customer will not buy the ball pen is 5 / 36
Q43: From a pack of 52 playing cards, Jacks and Kings of red colour and Queens and Aces of black colour are removed. The remaining cards are mixed, and a card is drawn at random. Find the probability that the drawn card is:
(A) a black queen.
(B) a card of red colour.
(C) a Jack of black colour.
(D) a face card. (CBSE 2017)
 View Answer
View Answer 
Ans: Number of cards removed = (2 + 2 + 2 + 2) = 8
Total number of remaining cards = (52 – 8) = 44
Now, there are 2 jacks and 2 kings of black colour and 2 queens and 2 aces of red colour left.
(A) Number of black queens = 0
∴ P(getting a black queen) = 0 / 44 = 0
(B) Number of red cards = 26 – 4 = 22
∴ P(getting a red card) = 22 / 44 = 1/ 2
(C) Number of jacks of black colour = 2
∴ P(getting a black jack) = 2 / 44 = 1 / 22
(D) We know that jacks, queens and kings are face cards.
∴ Number of remaining face cards = (2 + 2 + 2) = 6
∴ P(getting a face card) = 6/44 = 3 / 22
Previous Year Questions 2016
Q44: In the figure, a disc is shown on which a player spins an arrow twice. The function a / b is formed, where ‘a’ is the number of sectors on which the arrow stops on the first spin and ‘b’ is the number of the sectors in which the arrow stops on the second spin. On each spin, each sector has an equal chance of selection by the arrow. Find the probability that the fraction a / b > 1 (CBSE 2016)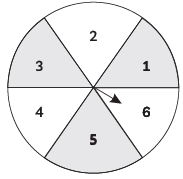
 View Answer
View Answer 
Ans: For a / b > 1,
When a = 1, b can not take any value.
When a = 2, b can take one value i.e., 1.
When a = 3, b can take two values i.e., 1, 2.
When a = 4, b can take three values i.e., 1, 2, 3.
When a = 5, b can take four values i.e., 1, 2, 3, 4.
When a = 6, b can take five values i.e., 1, 2, 3, 4, 5.
Here, total number of possible outcomes is same as when we throw a dice twice.
∴ Total possible outcomes = 36
∴ P ( ab > 1 ) = 1 + 2 + 3 + 4 + 536
= 15/36
= 5 / 12
Hence, the required probability is 5 / 12
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 14 Previous Year Questions - Probability
| 1. What are some common types of probability questions found in previous year exams? |  |
| 2. How can I effectively prepare for probability questions in competitive exams? |  |
| 3. Are there any specific formulas I should memorize for probability exams? |  |
| 4. How much weight does the probability section carry in competitive exams? |  |
| 5. Can you recommend some resources for practicing probability problems? |  |






















