Class 10 Maths Chapter 12 Previous Year Questions - Surface Area and Volumes
Previous Year Questions 2025
Q1: The radii 'r' of a sphere and that of the base of a cone are same. If their volumes are also same, then the height of the cone is:
(a) r
(b) 2r
(c) 3r
(d) 4r
 View Answer
View Answer 
Ans: (d)
Given, radius of sphere= radius of cone= r
Also, volume of sphere= volume of cone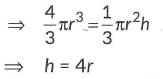
Q2: If the volumes of two cubes are in the ratio 8 : 125, then the ratio of their surface areas is :
(a) 8 : 125
(b) 4 : 25
(c) 2 : 5
(d) 16 : 25
 View Answer
View Answer 
Ans: Let a be side of one cube and b be side of another cube.
Given, ratio of their volumes= 8:125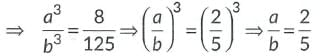
Ratio of their surface are 
Q3: If the radii of the bases of a cylinder and a cone are in the ratio 3: 4 and their heights are in the ratio 2 : 3, find the ratio of their volumes. (3 Marks)
 View Answer
View Answer 
Ans: Let r and R be the radius of cone and cylinder respectively and h and H be the height of cone and cylinder respectively.
The volume of cylinder (V1) = πR2H
Volume of cone (V2) = 
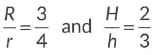
∴ Ratio of their volumes is given by V1/V2
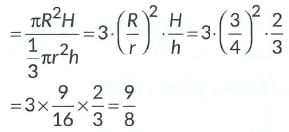
∴ Ratio of their volumes= 9: 8
Q4: Assertion (A) : If we join two hemispheres of same radius along their bases, then we get a sphere.
Reason (R) : Total surface area of a sphere of radius r is 3πr2.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
(c) Assertion (A) is true, but Reason (R) is false.
(d) Assertion (A) is false, but Reason (R)
 View Answer
View Answer 
Ans: (c)
Also, total surface area of a sphere of radius r is 4πr2.
So, Assertion is true, but Reason is false.
Q5: If a cone of greatest possible volume is hollowed out from a solid wooden cylinder, then the ratio of the volume of remaining wood to the volume of cone hollowed out is
(a) 1: 1
(b) 1: 3
(c) 2: 1
(d) 3: 1
 View Answer
View Answer 
Ans: (c)
Let rand h be the radius and height of cylinder respectively. 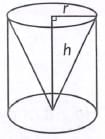
Volume of cone hollowed out = 1/3πr2h
Volume of remaining wood = Volume of cylinder - Volume of cone
Q6: A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. Also, find the a surface area of the toy. (Take π = 3.14)
 View Answer
View Answer 
Ans: Given, diameter of conical part = Diameter of hemispherical part= 4 cm
Radius of conical part (r) = radius of hemispherical part (r) = 4/2 = 2 cm.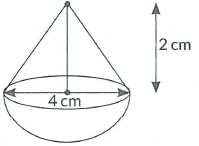
∴ Volume of toy= Volume of hemisphere+ Volume of cone = 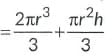
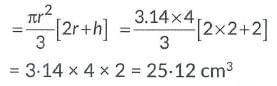
∴ Surface area of toy= Curved surface area of cone+ Curved surface area of hemisphere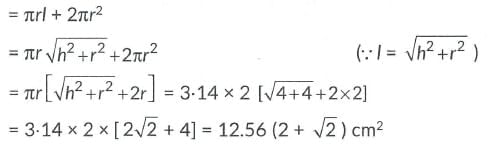
Q7: A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm, are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
 View Answer
View Answer 
Ans:
Let the radius and slant height of the cone be 3x and 5x respectively
∴ Radius (OB)= 3x and slant height (AB)= 5x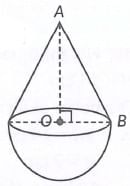 In ΔAOB,
In ΔAOB,
AB2 = OA2 + 0B2 [By Pythagoras theorem]
⇒ (5x)2 = (OA)2 + (3x)2
⇒ 25x2 = (OA)2 + 9x2
⇒ OA2 = 25x2 - 9x2 = 16x2
⇒ OA = 4x [Height of cone]
Volume of toy = Volume of hemi-sphere + Volume of right circular cone.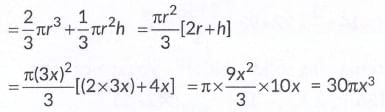
As, 30πx3 = 240π [Given]
⇒ x3 = 8
⇒ x= 2
∴ Total height of the toy = Height of cone + Radius of hemi-sphere
= 4x + 3x = 7x = 7 x 2 = 14 cm
Q8: From one face of a solid cube of side 14 cm, the largest possible cone is carved out. Find the volume and surface area of the remaining solid. (use π = 22/7, √5 = 2.2)
 View Answer
View Answer 
Ans: Height of largest cone= Side of cube
H = 14 cm
Diameter of largest cone= Side of cube
∴ 2R = 14cm
R=7cm
∴ Volume of the largest cone = 1/3πR2H
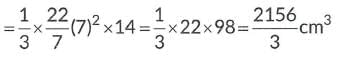
Volume of remaining solid = (side)3 - Volume of cone 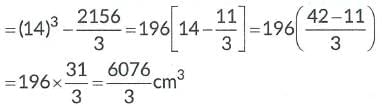
Slant height of cone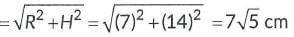
L = 15.4 cm
Surface area of remaining solid= 6(side)2 - πR2 + πRL 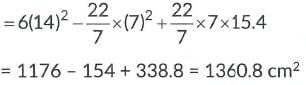
Q9: (a) A toy is in the form of a cone surmounted on a hemisphere. The cone and hemisphere have the same radii. The height of the conical part of the toy is equal to the diameter of its base. If the radius of the conical part is 5 cm, find the volume of the toy.
OR
(b) A cubical block is surmounted by a hemisphere of radius 3·5 cm. What is the smallest possible length of the edge of the cube so that the hemisphere can totally lie on the cube ? Find the total surface area of the solid so formed.
(5 Marks) (CBSE 2025)
 View Answer
View Answer 
Ans:(a)

(b)
Previous Year Questions 2024
Q3: A solid iron pole consists of a solid cylinder of height 200 cm and base diameter 28 cm, which is surmounted by another cylinder of height 50 cm and radius 7 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8 g mass.(4 & 5 Marks) (CBSE 2024)
 View Answer
View Answer 
Ans:
Here, the height of small cylinder (h1) = 50 cm
Radius of small cylinder r = 7 cm
Height of longer cylinder (h2) = 200 cm
Radius of longer cylinder (R) = 14 cm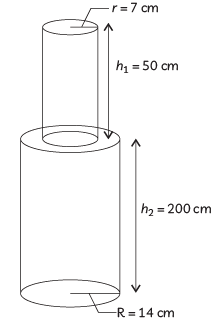 Volume of figure = Volume of small cylinder + volume of big cylinder
Volume of figure = Volume of small cylinder + volume of big cylinder
= πr²h₁ + πr²h₂
= π[r²h₁ + R²h₂]
= 227 [7 × 7 × 50 + 14 × 14 × 200]
= 227 × 49 × 50 [1 + 4]
= 22 × 7 × 50 × 171
= 1,30,900 cm3
Mass = Volume × Density
= 10,47,200 g
≈ 1047.2 kg
Q4: A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends. The length of the entire capsule is 14 mm and the diameter of the capsule is 4 mm, find its surface area. Also, find its volume. (4 & 5 Marks) (CBSE 2024)
 View Answer
View Answer 
Ans:
Here, two figures are combined, 2 hemisphere and cylinder.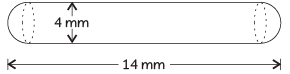 Radius of cylinder = radius of hemisphere
Radius of cylinder = radius of hemisphere
= 4/2 = 2 mm
Height of cylinder (h) = 14 – (2 + 2)
= 14 – 4 = 10 mm.
Surface area of capsule = curved surface area of two hemispheres + curved surface area of cylinder
= 2 × 2 πr² + 2πrh
= 2πr [2r + h]
= 2 × 227 × 2[4 + 10]
= 887 × 14
= 176 mm²
Volume of capsule = volume of 2 hemispheres + volume of cylinder
= 43 πr³ + πr²h
∴ Volume of 2 hemispheres = volume of a sphere
= πr² 43 (r + h)
= 227 × 2 × 2 × 43 × 2 + 10
= 227 × 4 × 83 + 10
= 227 × 4 × 38
= 88 × 3821 = 334421
= 159.24 mm³
Previous Year Questions 2023
Q5: The curved surface area of a cone having a height of 24 cm and a radius 7 cm, is (1 Mark) (2023)(a) 528 cm2
(b) 1056 cm2
(c) 550 cm2
(d) 500 cm2
 View Answer
View Answer 
Ans: (c)
We have, the height of cone. h = 24 cm and radius, r = 7 cm.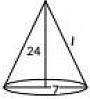
We know that,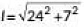 =
= 
= √625
= 25
Now. curved surface area = πrl
= 22/7 x 7 x 25
= 550 cm2
Q6: The curved surface area of a cylinder of height 5 cm is 94.2 cm2. The radius of the cylinder is (Take π = 3.14) (1 Mark) (2023)
(a) 2 cm
(b) 3 cm
(c) 2.9 cm
(d) 6 cm
 View Answer
View Answer 
Ans: (b)
Curved surface area of cylinder = 2πrh
⇒ 94.2 = 2 x 3 .14 x r x 5
⇒ r = 94.22x3.14x5
⇒ r = 3 cm
Q7: A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm.
 Find the total surface area of the article. (4/5/6 Marks) (CBSE 2023)
Find the total surface area of the article. (4/5/6 Marks) (CBSE 2023)
 View Answer
View Answer 
Ans: 
Radius of the cylinder (r) = 3.5 cm
Height of the cylinder (h) = 10 cm
Curved surface area = 2πrh
= ( 2 × 227 × 3510 × 10 ) cm2
= 220 cm2
Curved surface area of a hemisphere = 2πr2
∴ Curved surface area of both hemispheres
2 × 2πr2 = 4πr2 = ( 4 × 227 × 3510 × 3510 ) cm2
= 154 cm2
Total surface area of the Article
= (220 + 154) cm2
= 374 cm2
Q8: A room is in the form of a cylinder surmounted by a hemispherical dome. The base radius of the hemisphere is one-half the height of the cylindrical part. Find the total height of the room if it contains ( 140821 ) m3 of air. (Take π = 227 ) (3 Marks) (2023)
 View Answer
View Answer 
Ans:  Given, volume of the room = 140821 m3,
Given, volume of the room = 140821 m3,
π = 227
Radius of the hemisphere = r,
Height of the cylindrical part = h = 2r.
Volume of the room = Volume of the cylinder + Volume of the hemisphere
Volume of the cylinder = πr2h = πr2(2r) = 2πr3
Volume of the hemisphere = 23 πr3
Total volume = 2πr3 + 23 πr3 = 83 πr3
Equating total volume to 140821:
83 πr3 = 140821
83 × 227 × r3 = 140821
176r3 = 1408
r3 = 1408176
r3 = 8
r = 2
Total height = h + r = 2r + r = 3r = 3 × 2 = 6 meters
Final Answer:
The total height of the room is 6 meters.
Q9: An empty cone is of radius 3 cm and height 12 cm. Ice cream is filled in it so that the lower part of the cone which is (1/6)th of the volume of the cone is unfilled but the hemisphere is formed on the top. 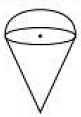 Find the volume of the ice cream. Take (π = 3.14) (3 Marks) (2023)
Find the volume of the ice cream. Take (π = 3.14) (3 Marks) (2023)
 View Answer
View Answer 
Ans: Radius of cone, r = 3 cm
Height of cone, h = 12 cm
Let x be the volume of unfilled part of cone.
Now, volume of cone, =
13 πr2h = 13 × 3.14 × (3)2 × 12
Volume of filled part of cone = Volume of cone - Volume of unfilled part of cone
= 13 × 3.14 × (3)2 × 12 − 16 × 13 × 3.14 × (3)2 × 12
= 13 × 3.14 × (3)2 × 12 × (1 - 16)
= 56 × 3.14 × (3)2 × 12 = 94.2 cm3
Now, volume of ice-cream = volume of filled part of cone + volume of hemisphere
= 94.2 + 23 × 3.14 × (3)3
= 150.72 cm3
Previous Year Questions 2022
Q10: The radius of the base and the height of a solid right circular cylinder are in the ratio 2:3 and its volume is 1617 cm3. Find the total surface area of the cylinder. Take [π = 22/7] (2022)
 View Answer
View Answer 
Ans: Given ratio of radius and height of the right circular cylinder = 2:3
Let radius (r) of the base be 2x and height(h) be 3x.
Volume of cylinder, V = πr2h
1617 = 227 × (2)2 × 3 × 3
⇒ 1617 = 227 × 4x2 × 3 × 3
1617 × 7
22 × 4 × 3 = x3
x3 = 7 × 7 × 72 × 2 × 2 = 72 cm.
Radius r = 2x = 2 × 72 = 7 cm
and height h = 3x = 3 × 72 = 212 cm
Total surface area of cylinder = 2πr (h + r)
= 2 × 22 × 77 × 212 + 7)
= 44 × 352 cm2
= 770 cm2
Q11: Case Study : John planned a birthday party for his younger sister with his friends. They decided to make some birthday caps by themselves and to buy a cake from a bakery shop. For these two items they decided on the following dimensions:
Cap : Conical shape with base circumference 44 cm and height 24 cm.
Cake : Cylindrical shape with diameter 24 cm and height 14 cm.
Based on the above information answer the following questions.
(a) How many square cm paper would be used to make 4 such caps?
(b) The bakery shop sells cakes by weight (0.5 kg, 1 kg, 1.5 kg. etc..}. To have the required dimensions how much cake should they order if 650 cm3 equals 100 g of cake? (2022)
 View Answer
View Answer 
Ans: Paper required to make four caps is 2,200 sq.cm.
Weight of the cake for required dimensions is 1kg.
Step-by-step explanation:
(a) Given the base circumference of the cone, c = 44 cm
Height of a cone, h = 24 cm.
Base circumference of the cone, c = 2πr = 44 cm
Thus, the radius of the cone is
r = 442 × 227 = 7 cm
The curved surface area of the cone is given by
CSA = πr √ h2 + r2
Substituting the values of h and r,
CSA = 227 × 7 × √ (24)2 + 72
= 22 × √ 576 + 49 = 22 × √ 625
= 22 × 25 = 550 sq. cm
Thus, to make one cap, 550 sq.cm of paper is required.
Then to make four caps, the required paper is
550 x 4 = 2200 sq. cm
Therefore, 2,200 sq.cm of paper is required to make four caps.
(b) Given the diameter of cylindrical shape cake, d = 24 cm
Height of cylindrical shape cake, h = 14 cm.
Radius of the cylindrical shape cake,
r = d2 = 242 = 12 cm
Volume of the cylinder is given by V = πr2h
Substituting the values of h and r,
V = 227 × (12)2 × 14
V = 227 × 144 × 14
= 22 × 144 × 2 = 6,336 cm3
The required volume of the cylindrical shape cake is 6,336 cm3.
Given 650 cm3 equals 100 g of cake.
Then the required weight of the cake is
6336650 × 100 = 974.76 g
Given the bakery shop sells cakes by weight of 0.5 kg, 1 kg, 1.5 kg, etc.
Since, 974.76 g ≈ 1 kg, therefore, the cake of 1 kg should be ordered for required dimensions.
Q12: Three cubes of side 6 cm each, are joined as shown in given figure. Find the total surface area of the resulting cuboid. (2022)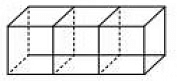
 View Answer
View Answer 
Ans: The dimension of the cuboids so formed are
length = 18 cm
breath = 6 cm and height = 6 cm.
Surface area of cuboids = 2 (l× b + b × h + l × h)
= 2 × (18 × 6 + 6 × 6+ 18 × 6)
= 504 cm2
Q13: Case Study : A 'circus' is a company of performers who put on shows of acrobats, downs etc to entertain people started around 250 years back, in open fields, now generally performed in tents. One such 'Circus Tent is shown below. The tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of cylindrical part are 9 m and 30 m respectively and height of conical part is 8 m with same diameter as that of the cylindrical part, then
The tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of cylindrical part are 9 m and 30 m respectively and height of conical part is 8 m with same diameter as that of the cylindrical part, then
find
(i) the area of the canvas used in making the tent.
(ii) the cost of the canvas bought for the tent at the rate Rs. 200 per sq. m. if 30 sq. m canvas was wasted during stitching. (CBSE Term-2 2022)
 View Answer
View Answer 
Ans: According to given information, we have the following figure.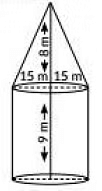
Clearly, the radius of conical part = radius of cylindrical part = 30/2 = 15 m = r ...(say)
Let h and H be the height of conical and cylindrical part respectively.
Then h = 8 m and H = 9 m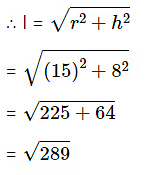
= 17 m
(i) The area of the canvas used in making the tent
= Curved surface area of cone + Curved surface area of cylinder
= πrl + 2πrH
= πr(l + 2H)
= 1650 m2
(ii) Area of canvas bought for the tent
= (1650 + 30) m2
= 1680 m2
Now, this cost of the canvas height for the tent
= ₹ (1680 × 200)
= ₹ 3,36,000
Previous Year Questions 2021
Q14: Water is being pumped out through a circular pipe whose internal diameter is 8 cm. If the rate of flow of water is 80 cm/s. then how many litres of water is being pumped out through this pipe in one hour? (2021) View Answer
View Answer 
Ans: Given diameter of circular pipe = 8 cm
So, radius of circular pipe = 4cm
Length of flow of water in one sec = 80 cm
length of flow of water in one hour = 80 x 60 x 60 cm=288000 cm=h
Volume of cylinderical pipe in one hour = πr2h
= 14482.28 litre [approx.]
14482.28 litres of water being pumped out through this pipe in 1 hr.
Previous Year Questions 2020
Q15: A solid spherical ball fits exactly inside the cubical box of side 2a. The volume of the ball is (2020)
(a) 163 πr3
(b) 16 πr3
(c) 323 πr3
(d) 43 πr3
 View Answer
View Answer 
Ans: (d)
Diameter of sphere = Distance between opposite faces of cube = 2a
Radius of sphere = a
So, volume of spherical ball = 43 πr3
= 43 πr3
Q16: The radius of a sphere (in cm) whose volume is 12 πcm3, is (2020)
(a) 3
(b) 3√3
(c) 32/3
(d) 31/3
 View Answer
View Answer 
Ans: (c)
Let radius of the sphere be r.
According to the question,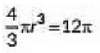
⇒ 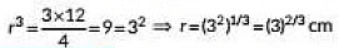
Q17: Two cones have their heights in the ratio 1: 3 and radii in the ratio 3 : 1 . What is the ratio of their volumes? (2020)
 View Answer
View Answer 
Ans: Let height of one cone be h and height of another cone be 3h. Radius, of one cone is 3r and radius of another cone is r.
∴ Ratio o f their volumes = 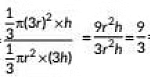
= 3 : 1
Q18: How many cubes of side 2 cm can be made from a solid cube of side 10 cm? (2020)
 View Answer
View Answer 
Ans: Let n be the number of solid cubes of 2cm made from a solid cube of side 10 cm.
∴ n x Volume of one small cube = Volume of big cube
⇒ n x (2)3 = (10)3
⇒ 8n = 1000
⇒ n = 1000/8
= 125
Thus, the number of solid cubes formed of side 2 cm each is 125.
Q19: A cone and a cylinder have the same radii but the height of the cone is 3 times that of the cylinder. Find the ratio of their volumes. (CBSE 2020)
 View Answer
View Answer 
Ans: Let the radius and the height of the cylinder are r and h respectively.
So, radios of t he cone is r and height of the cone is 3h.
∴ Volume of the cylinder = πr2h
So Volume of cone = 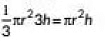
So, require ratio = 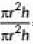
= 1 : 1
Q20: A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form a platform. Find the height of the platform. (Take π = 22/7) (2020)
 View Answer
View Answer 
Ans: Given that, the depth of the well is 14 m and the diameter is 3 m.
The width of the circular ring of the embankment is 4 m.
A figure is drawn below to visualize the shapes.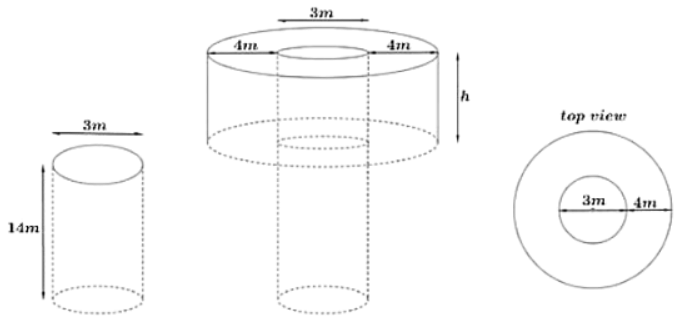
From the above figure, we can observe that the shape of the well will be cylindrical, and earth evenly spread out to form an embankment around the well in a circular ring will be cylindrical in shape (Hollow cylinder) having outer and inner radius.
Volume of the earth taken out from well = Volume of the earth used to form the embankment
Hence, Volume of the cylindrical well = Volume of the hollow cylindrical embankment
Let us find the volume of the hollow cylindrical embankment by subtracting volume of inner cylinder from volume of the outer cylinder.
Volume of the cylinder = πr2h where r and h are the radius and height of the cylinder respectively.
Depth of the cylindrical well, = h₁ = 14 m
Radius of the cylindrical well, = r = 3/2 m = 1.5 m
Width of embankment = 4 m
Inner radius of the embankment, r = 3/2 m = 1.5 m
Outer radius of the embankment, R = Inner radius + Width
R = 1.5 m + 4 m
= 5.5 m
Let the height of embankment be h
Volume of the cylindrical well = Volume of the hollow cylindrical embankment
πr2h1 = πR2h - πr2h
πr2h1 = πh (R2 - r2)
r2h1 = h (R - r )(R + r)
h = [(r2h1)/(R - r)(R + r)]
h = [((1.5 m)2 × 14 m)/(5.5 m - 1.5 m)(5.5 m + 1.5 m)]
= (2.25 m2 × 14 m)/(4m × 7 m)
= 1.125 m
Therefore, the height of the embankment will be 1.125 m.
Q21: In Figure, a solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. [Take π = 3.14] (2020)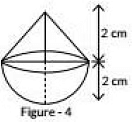
 View Answer
View Answer 
Ans: Given diameter of conical part = Diameter of hemispherical part = 4cm
∴ Radios of conical part (r) = Radius of hemispherical part (r) = 4/2 = 2 cm
Height of conical part (h) = 2 cm
∴ Volume of toy = Volume of hemisphere + volume of cone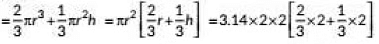
= 3 .14 x 4(1.33 + 0.66)= 3.14 x 4 x 1.99 cm3
Volume of the toy = 24.99 cm3
Q22: A solid toy is in the form of a hemisphere surmounted by a right circular cone of same radius. The height of the cone is 10 cm and the radius of the base is 7 cm. Determine the volume of the toy. Also find the area of the coloured sheet required to cover the toy. (Use π = 22/7 and √149 = 12.2) (2020)
 View Answer
View Answer 
Ans: Radius of the cone = Radius of the hemisphere = r = 7cm
Height of the cone, h = 10 cm
Now, volume of the toy = volume of hemisphere + volume of cone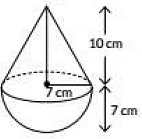
23 πr3 + 13 πr2 h = πr23 (2r + h)
= 13 × 227 × 7 × 7 (2×7 + 10)
= 22 × 7 × 243
= 1232 cm3
Curved surface area of the toy = Curved surface area of cone + Curved surface area of hemisphere
= πrl + 2πr2
= πr √ h2 + r2 + 2πr2
= 227 × 7 × √ (10)2 + 72 + 2πr2
= 22 × √ 100 + 49 + 14
= 22 × √ 149 + 14
= 22(12.2 + 14)
= 22 x 26.2
= 576.4 cm3
Q23: From a solid right circular cylinder of height 14 cm and base radius 6 cm, a right circular cone of same height and same base radius is removed. Find the volume of the remaining solid. (CBSE 2020)
 View Answer
View Answer 
Ans: Radius of cylinder = Radius of cone = r = 6 cm.
Height of cylinder = Height of cone = h = 14 cm
Volume of remaining solid = πr2h – 1/3πr2h
= 2/3πr2h
= 2/3 x 22/7 x 6 x 6 x 14
= 2 x 22 x 2 x 6 x 2
= 1056cm2
Hence, the volume of the remaining solid is 1056 cm2.
Previous Year Questions 2019
Q24: A solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 20 cm and the diameter of the cylinder is 7 cm. Find the total volume of the solid. (Use π = 22/7). (2019)
 View Answer
View Answer 
Ans: Radius of cylinderical part (r) = Radius of each spherical part(r) = 7/2 cm
Height of cylinderical part (h) = 20 - 7/2 - 7/2 = 13 cm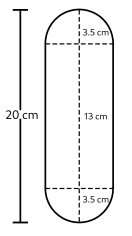
Now. Volume of the solid = Volume of cylinderical part + Volume of two hemispherical endsVolume of the solid = 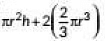
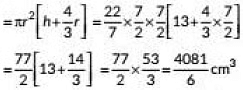
Volume of the solid = 680.17 cm3.
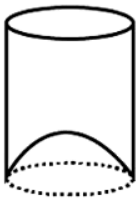
Q25: A juice seller was serving his customers using glasses as shown in the given figure. The inner diameter of the cylindrical glass was 5 cm but bottom of the glass had a hemispherical raised portion which reduced the capacity of the glass. lf the height of the glass was 10 cm, find the apparent and actual capacity of the glass {Use π = 3.14) (2019)
 View Answer
View Answer 
Ans: Base radius = 5/2 = 2.5 cm
Apparent capacity of glass = Volume of cylindrical portion
= πr2h
= 3.14 x (2.5)2 x 10
= 196.25 cm3
Actual capacity of the glass = Volume of cylinder - Volume of hemisphere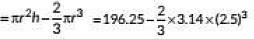
= 196.25 - 32.71
= 163.54 cm3
Q26: A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom of circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it. (Use π = 3.14) [CBSE 2019 (30/1/2)]
 View Answer
View Answer 
Ans: r = 12 cm, R = 20 cm, V = 12308.8 cm3
Volume of frustum = 13 πh (r2 + R2 + rR)
12308810 = 13 × 314100 × (144 + 400 + 240) × h
h = 123088 × 3 × 10314 × 784
h = 15 cm
l = √(h2 + r2) = √(225 + 64) = √289 = 17 cm
Area of metal sheet used = π(R + r)l + πr2
= π(20 + 12) x 17 + π x 144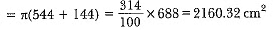
Hence, the height of the bucket is 15 cm and the area of the metal sheet used is 2160.32 cm2.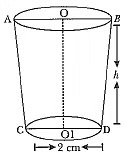
Q27: An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet (Fig). The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket, where we do not take into account the handle of the bucket. Also, find the volume of water the bucket can hold. 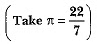 [CBSE 2019(30/5/1)]
[CBSE 2019(30/5/1)]
 View Answer
View Answer 
Ans: The total height of the bucket = 40 cm, which includes the height of the base. So, the height of the frustum of the cone = (40 - 6) cm = 34 cm.
Therefore, the slant height of the frustum,
l = √(R2 + (r1 - r2)2)
where, r1 = 452 cm = 22.5 cm
r2 = 252 cm = 12.5 cm and h = 34 cm
So, l = √(342 + (22.5 - 12.5)2) = √(342 + 102) = 35.44 cm
Area of the metallic sheet used
Curved surface area of frustum of cone + Area of circular base + Curved surface area of cylinder
= [π × 35.44 (22.5 + 12.5) + π × (12.5)2 + 2π × 12.5 × 6] cm2
= 227 × (1240.4 + 156.25 + 150) cm2
= 4860.9 cm2
Now, the volume of water that the bucket can hold (also, known as the capacity of the bucket)
Volume of frustum:
= 13 π × h (r12 + r22 + r1r2)
= 13 × 227 × 34 × (22.52 + 12.52 + 22.5 × 12.5) cm3
= 13 × 227 × 34 × 943.75 = 33615.48 cm3
= 33.62 litres (approx.)
Q28: A cylindrical bucket, 32 cm high and with a radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
OR
A girl empties a cylindrical bucket, full of sand, of base radius 18 cm and height 32 cm, on the floor to form a conical heap of sand. If the height of this conical heap is 24 cm, then find its slant height correct up to one place of decimal. [CBSE (E) 2014, 2019 (30/5/1)]
 View Answer
View Answer 
Ans: 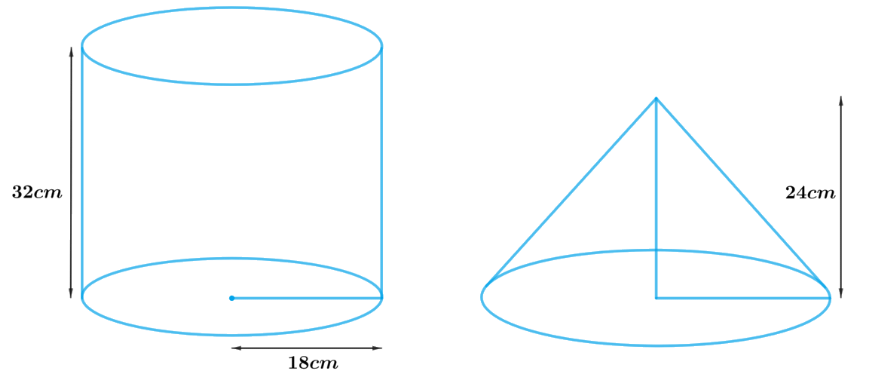 We have,
We have,
Radius of cylindrical bucket =18 cm
Height of cylindrical bucket = 32 cm
And the height of conical heap = 24 cm
Let the radius of the conical heap be r cm
Volume of the sand = volume of the cylindrical bucket
= πr2h = π x (18)2 x 32
Now, volume of conical heap 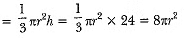
Here, volume of the conical heap will be equal to the volume of sand
∴ 8πr2 = π x (18)2 x 32
⇒ r2 = 18 x 18 x 4 = (18)2 x (2)2
⇒ r2 = (36)2 or r = 36 cm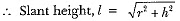
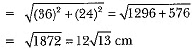
Previous Year Questions 2018
Q29: The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find the area of the metal sheet used to make the bucket. [Use π = 3.14] [CBSE 2018] View Answer
View Answer 
Ans: 
For bucket,
Upper diameter (D) = 30 cm
∴ Radius (R) = 302 = 15 cm
Lower diameter (d) = 10 cm
Radius (r) = 102 = 5 cm
Height of bucket (h) = 24 cm
The area of the metal sheet used = CSA of the frustum (bucket) + Area of bottom part (base)
= π(R + r)l + πr2
= π(R + r) × √(h2 + (R - r)2) + πr2
[∵ Slant height (l) = √(h2 + (R - r)2)]
= 3.14 × (15 + 5) × √(242 + (15 - 5)2) + 3.14 × (5)2
= 3.14 × 20 × √(576 + 100) + 3.14 × 25
= 62.8 × √676 + 78.5
= 62.8 × 26 + 78.5
= 1632.8 + 78.5 = 1711.3 cm2
Previous Year Questions 2017
Q30: A metallic right circular cone 20 cm high whose vertical angle is 60° which is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter 1/16 cm, find the length of the wire. [NCERT, CBSE (F) 2017] View Answer
View Answer 
Ans: Let VAB be the metallic right circular cone of height 20 cm. Suppose this cone is cut by a plane parallel to its base at a point O' such that VO' = O' O i.e., O' is the midpoint of VO.
Let r1 and r2 be the radii of circular ends of the frustum ABB' A'.
Now, in ΔVOA and VO' A', we have
⇒ tan 30° = OAVO and tan 30° = O'A'V'O'
⇒ 1√3 = r120 and 1√3 = r210
⇒ r1 = 20√3 and r2 = 10√3
∴ Volume of the frustum = 13 πh (r12 + r22 + r1r2)
= 13 × π × 10 × [ (20/√3)2 + (10/√3)2 + (20/√3 × 10/√3) ]
= 10π3 × [400/3 + 100/3 + 200/3]
= 10π3 × 7003 cm3
Let the length of wire of diameter 1/16 cm be l cm. Then,
Volume of metal used in wire
= π × (1/32)2× l = πl/1024 cm3
Since the frustum is recast into a wire of length l cm and diameter 1/16 cm,
∴ Volume of the metal used in wire = volume of the frustum
⇒ πl1024 = 7000π9
⇒ l = 7000 × 10249
= 796144.4 cm = 7964.444 m
Q31: A solid metallic cylinder of diameter 12 cm and height 15 cm is melted and recast into toys each in the shape of a cone of radius 3 cm and height 9 cm. Find the number of toys so formed. [AI 2017 (C)]
 View Answer
View Answer 
Ans: Diameter of metallic cylinder = 12 cm
∴ Radius of metallic cylinder (r) = 6 cm
Height (h) = 15 cm
Volume of cylinder = πr2h = π(6)2 x 15 cm3
Radius of cone = 3 cm
Height of cone = 9 cm
Volume of cone = 1/3 π(3)2 x 9 = 3 x 9π cm3
Number of toys so formed = 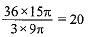
If the question is “A tent is in the form of a cylinder surmounted by a cone. Find the capacity of the tent and the cost of canvas for making the tent at Rs 100 per sq.m.”, then the solution is given as “Tent is a combination of a cylinder and a cone. For capacity
∴ Volume (capacity) of the tent = Volume of the cylindrical part + Volume of the conical part
For the cost of the canvas, we find the total surface area.
Total surface area = Curved area of the cylindrical part + Curved surface area of the conical part
Now, proceed to find its cost.”
Note: Don’t solve as “Total surface area of canvas = Total surface area of cylinder + Total surface area of a cone and proceed further"
This is the wrong solution.
Q32: The 3/4th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with an internal radius of 10 cm. Find the height of water in a cylindrical vessel. [Delhi 2017]
 View Answer
View Answer 
Ans: Radius of conical vessel (r) = 5 cm
Height of conical vessel (h) = 24 cm
Radius of cylindrical vessel (R) = 10 cm
Let H be the height of water in the cylindrical vessel.
Now, the total volume of the conical vessel
= 13 πr2h = 13 × 227 × (5)2 × 24 cm3
= 22 × 25 × 247 × 3 cm3
According to the question,
3/4 of the volume of water from the conical vessel is emptied into the cylindrical vessel.
⇒ 34 × Volume of conical vessel = Volume of water in the cylindrical vessel
⇒ 34 × 22 × 25 × 247 × 3 = πR2H
⇒ 3 × 22 × 25 × 244 × 7 × 3 = 227 × (10)2 × H
⇒ 25 × 6 = 10 × 10 × H
⇒ H1 = 25 × 610 × 10
⇒ H = 1.5 cm
∴ Height of water in the cylindrical vessel = 1.5 cm
Q33: In a rain-water harvesting system, the rainwater from a roof of 22 m x 20 m drains into a cylindrical tank having a diameter of base 2 m and height of 3.5 m. If the tank is full, find the rainfall in cm. [AI 2017]
 View Answer
View Answer 
Ans: 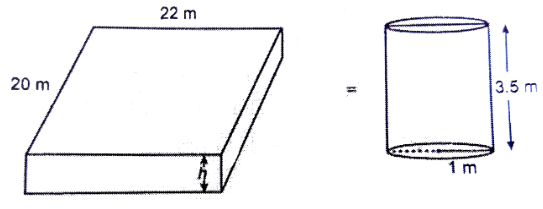 Length of roof (l) = 22 m
Length of roof (l) = 22 m
Breadth of roof (b) = 20 m
Let the height of water column collected on roof= hm
∴ Volume of standing water on rooftop = lbh
= (22 x 20 x h) m3
This water is taken into a cylindrical tank of diameter of base 2 m and height 3.5 m.
Tank gets completely filled with this amount of water.
⇒ Volume of water from roof-top = Volume of cylinder
Diameter of tank = 2 m
∴ Radius of tank = 2/2 = 1 m
⇒ Volume of tank = πr2h
= 227 × (1)2 × 3.5 m3
A.T.Q.
(22 × 20 × h) m3 = 227 × 1 × 3.5 m3
⇒ h = 22 × 3.57 × 22 × 20
⇒ h = 777 × 22 × 30
= 0.025 m = 2.5 cm
Hence rainfall is 2.5 cm.
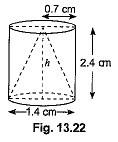
Q34: From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2. [CBSE (AI) 2017]
 View Answer
View Answer 
Ans: We have,
Radius of the cylinder = 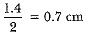 Height of the cylinder = 2.4 cm
Height of the cylinder = 2.4 cm
Also, radius of the cone = 0.7 cm and height of the cone = 2.4 cm
Now, slant height of the cone =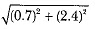
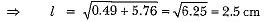
∴ Total surface area of the remaining solid
= curved surface area of cylinder + curved surface area of the cone + area of upper circular base of the cylinder.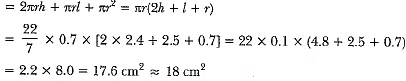
Q35: A circus tent is in the shape of a cylinder surmounted by a conical top of the same diameter. If their common diameter is 56 m, the height of the cylindrical part is 6 m and the total height of the tent above the ground is 27 m, find the area of canvas used in making the tent. (CBSE 2017)
 View Answer
View Answer 
Ans: 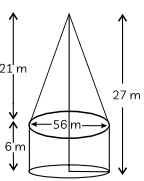
Total height of the tent above the ground = 27 m
Height of the cylindrical part,
h1 = 6 m
Height of the conical part,
h2 = 21 m
Diameter = 56 m
Radius = 28 m
Curved surface area of the cylinder, CSA1
= 2πrh = 2π × 28 × 6 = 336π
Curved surface area of the cone, CSA2
= πrl = π × 28 × √ h22 + r2
= π × 28 × √ 212 + 282
= 28π × √ 441 + 784
= 28π × 35
= 980π
Total curved surface area = CSA of cylinder + CSA of cone
= CSA1 + CSA2
= 336π + 980π
= 1316π
= 4136 m2
Previous Year Questions 2016
Q36: A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by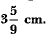 Find the diameter of the cylindrical vessel. [CBSE (AI) 2016]
Find the diameter of the cylindrical vessel. [CBSE (AI) 2016] View Answer
View Answer 
Ans: Volume of sphere = 43 π(6)3 cm3
Volume of water rise in cylinder
= πr2 329 cm3
∴ πr2 329 = 43 π(6)3
⇒ r2 = 4 × 2 × 36 × 932 = 81
⇒ r = 9 cm
Previous Year Questions 2015
Q37: Two spheres of the same metal weigh 1 kg and 7 kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the new sphere. [CBSE (F) 2015] View Answer
View Answer 
Ans: Volume of the smaller sphere
= 43 πr3 = 43 π(3)3 = 43 π(27) = 36π
Volume of smaller sphere × density = mass
∴ 36π (density of metal) = 1
Density of metal = 136π
∴ Volume of bigger sphere × density = mass
= 43 π (R)3 × 136π = 7
R3 = 7 × 36 × 34 = 7 × 9 × 3
(i) Volume of new sphere = volume of smaller sphere + volume of bigger sphere
= 43 π(R')3 = 43 πr3 + 43 πR3 (where R' is the radius of the new sphere)
= 43 π(3)3 + 43 π(7 × 9 × 3) [using (i)]
= 43 π [33 + 7 × 9 × 3]
(R')3 = [33 + 7 x 33]
(R')3 = 33(l + 7)
(R')3 = 33 x 8
(R')3 = 33 x 23
R' =3 x 2
R' = 6 cm
∴ Diameter of new sphere =12 cm.
Q38: A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of each bottle, if 10% liquid is wasted in this transfer. [CBSE (AI) 2015]
 View Answer
View Answer 
Ans: Radius of hemispherical bowl, R = 36/2 = 18 cm
Radius of cylindrical bottle, r = 6/2 = 3 cm
Let height of cylindrical bottle = h
Since 10% liquid is wasted, therefore only 90% liquid is filled into 72 cylindrical bottles.
∴ The volume of 72 cylindrical bottles = 90% of the volume in the bowl
⇒ 72 × πr2h = 90% of 23 πR3
72 × π × 3 × 3 × h = 90100 × 23 × π × 18 × 18 × 18
h = 90 × 2 × π × 18 × 18 × 18100 × 3 × π × 72 × 3 × 3
h = 275 = 5.4 cm
Q38: A cone with radius 10 cm is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base. Compare the volumes of the two parts. [CBSE (AI) 2015]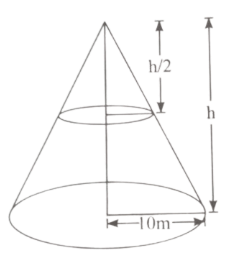
 View Answer
View Answer 
Ans: Let.BC = r cm, DE = 10 cm
Since B is the mid-point of AD and BC is parallel to DE, therefore C is the mid-point of AE.
∴ AC = CE
Also, ΔABC ~ ΔADE
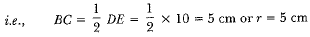
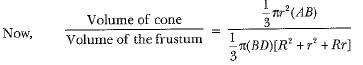
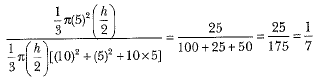
∴ The required ratio = 1 : 7.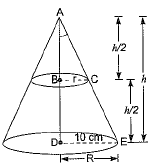
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 12 Previous Year Questions - Surface Area and Volumes
| 1. What are surface areas and volumes, and why are they important in mathematics? |  |
| 2. How do I calculate the surface area of a cube? |  |
| 3. What is the formula for the volume of a cylinder? |  |
| 4. Can you explain how to find the surface area of a sphere? |  |
| 5. What role do surface areas and volumes play in real-life applications? |  |

















