NEET Previous Year Questions (2014-2025): Mechanical Properties of Fluids | Physics Class 11 PDF Download
2025
Q1: Consider a water tank shown in the figure. It has one wall at x = L and can be taken to be very wide in the z direction. When filled with a liquid of surface tension S and density ρ, the liquid, surface makes angle θ0(θ0≪1) with the x - axis at x = L. If y (x) is the height of the surface then the equation for y (x) is: [2025]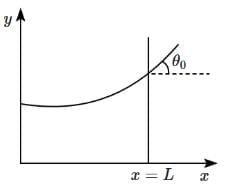
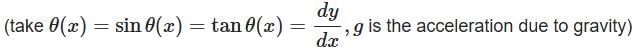
(a) 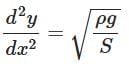
(b) 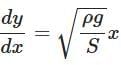
(c) 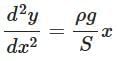
(d) 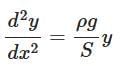
Ans: (d)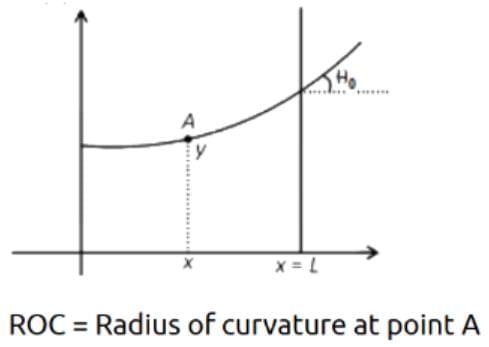
Curvature = 1 / ROC = |d2y/dx2| / (1 + (dy/dx)2)3/2 ≈ |d2y/dx2| / (1 + 0)3/2 = d2y/dx2
(dy/dx) ≈ tan θ ≈ 0 (small angle approximation)
Change in pressure, ΔP = S × curvature
ΔP = S × d2y/dx2
Also, ΔP = ρgy
⇒ ρgy = S × d2y/dx2
⇒ d2y/dx2 = (ρg / S) y
2024
Q1: A thin flat circular disc of radius 4.5 cm is placed gently over the surface of water. If the surface tension of water is 0.07 Nm−1, then the excess force required to take it away from the surface is: [2024]
(a) 198 N
(b) 1.98 mN
(c) 99 N
(d) 19.8 mN
Ans: (d)
The excess force required to remove a thin flat circular disc from the surface of water can be calculated using the formula for the force due to surface tension:
Force (F) = 2πr × T
Where:
- r is the radius of the disc,
- T is the surface tension of the water.
Given:
r = 4.5 cm = 0.045 m,
T = 0.07 N/m.
Now, substituting the values into the formula:
F = 2π × 0.045 × 0.07
F ≈ 2 × 3.1416 × 0.045 × 0.07
F ≈ 0.0198 N
Converting to milli Newtons (mN):
F ≈ 19.8 mN
So, the correct answer is:
(d) 19.8 mN.
Q2: A wire of length L and radius r ( r ≪ L ) is kept floating on the surface of a liquid of density ρ . The maximum radius of the wire for which it may not sink is: (the surface tension of liquid is T) [2024]
(a) √T/ρg
(b) √2T/ρg
(c) √2Tρ/π
(d) √2T/πρg
Ans: (d)
To determine the maximum radius of a wire floating on the surface of a liquid, we can use the concept of surface tension. The force due to surface tension must balance the weight of the wire in order to prevent it from sinking.
Surface Tension Force:
The total force due to surface tension F is given by:
F = 2πrL × T
Where:
- r is the radius of the wire,
- L is the length of the wire,
- T is the surface tension of the liquid.
Weight of the Wire:
The weight of the wire W is given by:
W = ρg V
Where:
- ρ is the density of the liquid,
- g is the acceleration due to gravity,
- V = πr²L is the volume of the wire.
So, the weight of the wire becomes:
W = ρg × πr²L
Condition for Floating:
For the wire to float without sinking, the surface tension force must be equal to the weight of the wire:
2πrL ×T = ρg × πr²L
Now, canceling out common terms:
2T = ρg × r
Solving for r:
r = 2T / (ρg)
Maximum Radius:
Thus, the maximum radius of the wire for which it may not sink is:
r = √(2T / (πρg))
So, the correct answer is: (d) √(2T / πρg).
Q3: The pressure experienced by a swimmer 20 m below the water surface in a lake is appropriately:
(Given density of water = 103 kgm−3, g = 10 ms−2 and 1 atm = 105 Pa) [2024]
(a) 1 atm
(b) 2 atm
(c) 3 atm m
(d) 4 atm
Ans: (c)
To calculate the pressure experienced by the swimmer at a depth of 20 m below the water surface, we need to use the formula for the pressure at a depth in a fluid:
P = P₀ + ρgh
Where:
- P is the total pressure at depth,
- P₀ is the atmospheric pressure at the surface (1 atm),
- ρ is the density of the water,
- g is the acceleration due to gravity,
- h is the depth below the surface.
Given:
- ρ = 10³ kg/m³ (density of water),
- g = 10 m/s² (acceleration due to gravity),
- h = 20 m (depth),
- P₀ = 1 atm = 10⁵ Pa (atmospheric pressure).
Now, we calculate the pressure at the depth:
First, calculate the hydrostatic pressure due to the water column:
ρgh = (10³ kg/m³) × (10 m/s²) × (20 m) = 2 × 10⁵ Pa
Total pressure at the depth is the sum of atmospheric pressure and the hydrostatic pressure:
P = 1 atm + 2 × 10⁵ Pa
Since 1 atm = 10⁵ Pa, we have:
P = 10⁵ Pa + 2 × 10⁵ Pa = 3 × 10⁵ Pa
Now, convert the pressure to atmospheres:
P = 3 × 10⁵ Pa / 10⁵ Pa = 3 atm
Thus, the correct answer is: (c) 3 atm.
Q4: An ideal fluid is flowing in a non-uniform cross-sectional tube XY (as shown in the figure) from end X to end Y. If K1 and K2 are the kinetic energies per unit volume of the fluid at X and Y respectively, the correct relationship between K1 and K2 is: [2024]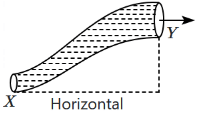 (a) K1 = K2
(a) K1 = K2
(b) 2K1 = K2
(c) K1 > K2
(d) K1 < K2
Ans: (c)
To solve this problem, we need to apply the principle of conservation of mechanical energy (also known as Bernoulli's theorem) and understand the relationship between velocity and kinetic energy in a fluid flow.
Bernoulli's Principle:
Bernoulli's equation states that for an ideal, incompressible fluid flowing through a non-uniform cross-sectional tube, the total mechanical energy (sum of pressure energy, kinetic energy, and potential energy) remains constant along a streamline.
The equation is given by:
P + ½ ρv² + ρgh = constant
Where:
- P is the pressure of the fluid,
- ρ is the density of the fluid,
- v is the velocity of the fluid,
- g is the acceleration due to gravity,
- h is the height of the fluid at a point (potential energy term).
In the given problem, K1 and K2 represent the kinetic energy per unit volume at points X and Y. The kinetic energy per unit volume is:
K = ½ ρv²
Now, we are given that the cross-section of the tube is non-uniform, which means the velocity of the fluid will change as it moves from one section to another.
Relationship Between Kinetic Energy and Velocity:
Since the tube is non-uniform, the velocity of the fluid will change based on the cross-sectional area. According to the continuity equation:
A₁v₁ = A₂v₂
Where:
- A₁ and A₂ are the cross-sectional areas at points X and Y,
- v₁ and v₂ are the velocities of the fluid at points X and Y.
If the cross-sectional area at point Y is smaller than at point X, the velocity of the fluid will increase at point Y (since the fluid must maintain the same flow rate). This implies that the kinetic energy at point Y (K2) will be higher than at point X (K1).
Therefore, based on the continuity equation and Bernoulli's principle, the correct relationship between the kinetic energy per unit volume at points X and Y is:
K1 > K2
This is because, at point X, the velocity is lower (due to a larger cross-sectional area), and at point Y, the velocity is higher (due to a smaller cross-sectional area), which leads to a greater kinetic energy at X.
Thus, the correct answer is: (c) K1 > K2.
2023
Q1: The venturi-meter works on [2023]
(a) Huygen’s principle
(b) Bernoulli’s principle
(c) The principle of parallel axes
(d) The principle of perpendicular axes
Ans: (b)
Venturi-meter works on the Bernoulli’s principle.
Q2: The amount of energy required to form a soap bubble of radius 2 cm from a soap solution is nearly: (the surface tension of soap solution 0.03 Nm− 1) [2023]
(a) 50.1 × 10−4 J
(b) 30.16 × 10−4 J
(c) 5.06 × 10−4 J
(d) 3.01 × 10−4 J
Ans: (d)
To calculate the energy required to form a soap bubble, we need to consider the work done to increase the surface area of the bubble.
When a soap bubble is formed, it has two surfaces (inner and outer) exposed to the air. The energy required is related to the surface area of the bubble and the surface tension of the soap solution.
Formula for Energy:
The energy required to form a soap bubble is given by the formula:
Energy (E) = 4πr² × T
Where:
- r is the radius of the bubble,
- T is the surface tension of the soap solution.
Since a soap bubble has two surfaces, the total surface area exposed is 2 * 4πr². The formula for the energy required to form a soap bubble is:
E = 8πr² × T
Given:
- r = 2 cm = 0.02 m,
- T = 0.03 N/m (surface tension).
Now, substituting the given values into the formula:
E = 8π × (0.02)² × 0.03
E = 8π × 0.0004 × 0.03
E = 8 × 3.1416 × 0.000012
E ≈ 3.01 × 10⁻⁴ J
Thus, the correct answer is: (d) 3.01 × 10⁻⁴ J.
Q3: Which of the following statements is not true? [2023]
(a) The coefficient of viscosity is a scalar quantity.
(b) Surface tension is a scalar quantity.
(c) Pressure is a vector quantity.
(d) Relative density is a scalar quantity.
Ans: (c)
(a) The coefficient of viscosity is a scalar quantity - TRUE
The coefficient of viscosity (η) represents the internal friction of a fluid and has only magnitude, no direction.
(b) Surface tension is a scalar quantity - TRUE
Surface tension is measured as energy per unit area or force per unit length, and it has only magnitude, no direction.
(c) Pressure is a vector quantity - FALSE
Pressure is defined as force per unit area. While force is a vector, when we calculate pressure, we consider only the magnitude of the force acting perpendicular to the surface area. Pressure at a point acts equally in all directions (Pascal's principle) and is characterized only by its magnitude, making it a scalar quantity.
(d) Relative density is a scalar quantity - TRUE
Relative density (or specific gravity) is the ratio of the density of a substance to a reference substance (usually water). Being a ratio of two scalar quantities, it is also a scalar quantity.
Therefore, option (c) is the incorrect statement, making it the correct answer to this question.
Q4: The viscous drag acting on a metal sphere of diameter 1 mm, falling through a fluid of viscosity 0.8 Pa-s with a velocity of 2 m s–1 is nearly equal to: [2023]
(a) 15 × 10−3 N
(b) 30 × 10−3 N
(c) 1.5 × 10−3 N
(d) 20 × 10−3 N
Ans: (a)
To calculate the viscous drag on a metal sphere falling through a fluid, we use Stokes' Law, which is given by the formula:
F = 6πηrv
Where:
- F is the viscous drag force (in N),
- η is the dynamic viscosity of the fluid (in Pa-s),
- r is the radius of the sphere (in m),
- v is the velocity of the sphere (in m/s).
Given:
- Diameter of the sphere = 1 mm = 1 × 10^-3 m
- Radius, r = (1 × 10^-3 m) / 2 = 0.5 × 10^-3 m = 5 × 10^-4 m
- Viscosity, η = 0.8 Pa-s
- Velocity, v = 2 m/s
Calculation:
Substitute the given values into the formula:
F = 6π × 0.8 × (5 × 10-4) × 2
F = 6 × 3.14 × 0.8 × 5 × 10-4 × 2
F = 15.072 × 10-3 N
Thus, the viscous drag is approximately 15 × 10-3 N.
Final Answer: (a) 15 × 10−3 N
2022
Q1: If a soap bubble expands, the pressure inside the bubble [2022]
(a) Increases
(b) Remains the same
(c) Is equal to the atmospheric pressure
(d) Decreases
Ans: (d)
Excess pressure inside the bubble =
P = P0 + 4T/R
as ‘R’ increases ‘P’ decreases
Q2: A spherical ball is dropped in a long column of a highly viscous liquid. The curve in the graph shown, which represents the speed of the ball (v) as a function of time (t) is [2022]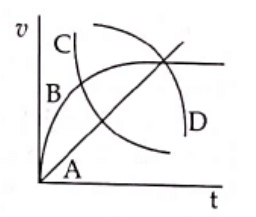
(a) B
(b) C
(c) D
(d) A
Ans: (a)
Initial speed of ball is zero and it finally attains terminal speed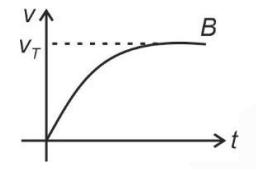
2021
Q1: The velocity of a small ball of mass M and density d, when dropped in a container filled with glycerine becomes constant after some time. If the density of glycerine is d/2, then the viscous force acting on the ball will be: [2021]
(a) 3/2Mg
(b) 2Mg
(c) Mg/2
(d) Mg
Ans: (c)
Mass = M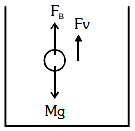
Density of ball = d
Density of glycerine = d/2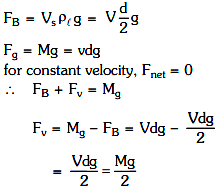
2020
Q1: A barometer is constructed using a liquid (density = 760 kg/m3 ). What would be the height of the liquid column, when a mercury barometer reads 76 cm? (Density of mercury = 13600 kg/m3 ) [2020]
(a) 1.36 m
(b) 13.6 m
(c) 136 m
(d) 0.76 m
Ans: (b)
Density of liquid, ρl = 760 kg /m3
Density of mercury, ρm = 13600 kg /m3
Height of liquid column in mercury barometer,
hm = 76 cm = 0.76 m
If height of liquid in liquid column be hl , then
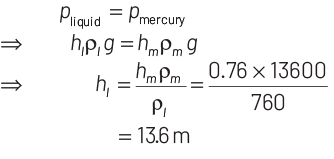
Q2: A liquid does not wet the solid surface if angle of contact is [2020]
(a) equal to 45°
(b) equal to 60°
(c) greater than 90°
D zero
Ans: (c)
A liquid does not wet the solid surface, if the angle of contact is obtuse i.e., θ > 90º.
2019
Q1: A soap bubble, having radius of 1 mm, is blown from a detergent solution having a surface tension of 2.5 × 10-2 N/m. The pressure inside the bubble equals at a point Z0 below the free surface of water in a container. Taking g = 10 m/s2, density of water = 103 kg/m3, the value of Z0 is [2019]
(a) 100 cm
(b) 10 cm
(c) 1 cm
(d) 0.5 cm
Ans: (c)
Excess pressure = 4T/R, Gauge pressure
Q2: A small hole with area area of cross-section 2 mm2 is present near the bottom of a fully filled open tank of height 2 m. Taking g = 10 m/s2, the rate of flow of water through the open hole would be nearly [2019]
(a) 12.6 × 10–6 m3/s
(b) 8.9 × 10–6 m3/s
(c) 2.23 × 10–6 m3/s
(d) 6.4 × 10–6 m3/s
Ans: (a)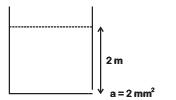
Rate of liquid flow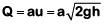
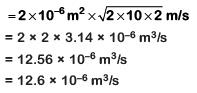
2018
Q1: A small sphere of radius 'r' falls from rest in a viscous liquid. As a result, heat is produced due to viscous force. The rate of production of heat when the sphere attains its terminal velocity, is proportional to:- [2018]
(a) r3
(b) r2
(c) r5
(d) r4
Ans: (c)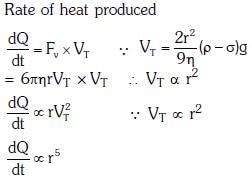
2017
Q1: A U tube with both ends open to the atmosphere, is partially filled with water. Oil, which is immiscible with water, is poured into one side until it stands at a distance of 10 mm above the water level on the other side. Meanwhile the water rises by 65 mm from its original level (see diagram). The density of the oil is:- [2017]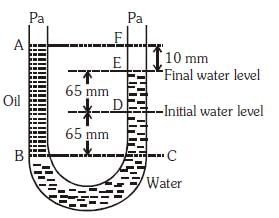
(a) 425 kg m–3
(b) 800 kg m–3
(c) 928 kg m–3
(d) 650 kg m–3
Ans: (c)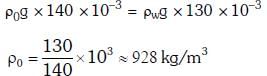
2016
Q1: Two non-mixing liquids of densities ρ and nρ (n > 1) are put in container. The height of each liquid is h. A solid cylinder of length L and density d is put in this container. The cylinder floats with its axis vertical and length pL (p < 1) in the denser liquid. The density d is equal to [2016]
(a) {1 + (n - 1)p}ρ
(b) {1 + (n + 1)p}ρ
(c) {2+(n + 1)p}ρ
(d) {2 + (n - 1)p}ρ
Ans: (a)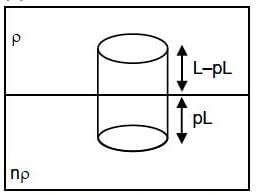
weight of body = upthrust by the two liquids
If A = Area of section then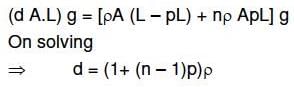
2015
Q1: The approximate depth of an ocean is 2700 m. The compressibility of water is 45.4 x 10-11 Pa-1 and density of water is 103 kg/m3. What fractional compression of water will be obtained at the bottom of the ocean? [2015]
(a) 1.4 x 10-2
(b) 0.8 x 10-2
(c) 1.0 x 10-2
(d) 1.2 x 10-2
Ans: (d)

Q2: A wind with speed 40 m/s blows parallel to the roof of a house. The area of the roof is 250 m2. Assuming that the pressure inside the house is atmospheric pressure, the force exerted by the wind on the roof and the direction of the force will be:
(Pair = 1.2 kg/m3) [2015]
(a) 2.4 x 105 N, downwards
(b) 4.8 x 105 N, downwards
(c) 4.8 x 105 N, upwards
(d) 2.4 x 105 N, upwards
Ans: (d)
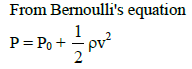
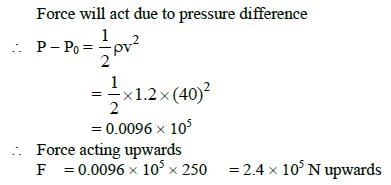
2014
Q1: A certain number of spherical drops of a liquid of radius ‘r’ coalesce to form a single drop of radius ‘R’ and volume ‘V’. If ‘T’ is the surface tension of the liquid, then: [2014]
(a) 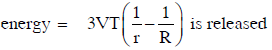
(b) energy is neither released nor absorbed
(c) 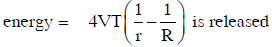
(d) 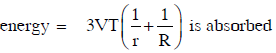
Ans: (a)
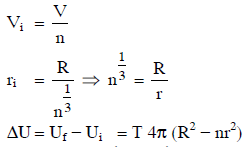
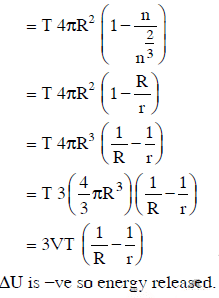
|
96 videos|367 docs|98 tests
|
FAQs on NEET Previous Year Questions (2014-2025): Mechanical Properties of Fluids - Physics Class 11
| 1. What are the different types of mechanical properties of fluids? |  |
| 2. How does viscosity affect the flow of fluids? |  |
| 3. What is the significance of surface tension in fluid mechanics? |  |
| 4. How does compressibility affect the behavior of fluids under pressure? |  |
| 5. What is the bulk modulus of a fluid and how does it relate to its compressibility? |  |

















