NEET Previous Year Questions (2014-2025): Waves | Physics Class 11 PDF Download
2025
Q1: A pipe open at both ends has a fundamental frequency f in air. The pipe is now dipped vertically in a water drum to half of its length. The fundamental of the air column is now equal to: (NEET 2025)
(a) 3f/2
(b) 2f
(c) f/2
(d) f
Ans: (d)
For a pipe of length L open at both ends, the fundamental frequency (f) in air is given by the equation:
f = v/λ = (v / 2L)
⇒ λ =2L
Now, when the pipe is dipped vertically in water and half of it is submerged, the length of the air column is halved.
⇒ L' = L/2
⇒ λ' =4L' = 2L
Hence, f' = v / λ' = v / 2L = f
2024
Q1: Given below are two statements: (NEET 2024)
Assertion (A): A glass tube partially filled with water represents an open organ pipe.
Reason (R): The open end corresponds to an antinode and the end in contact with water, to a node.
In the light of the above statements, choose the correct answer from the options given below:
(a) Both (A) and (R) are True and (R) is the correct explanation of (A).
(b) Both (A) and (R) are True and (R) is not the correct explanation of (A).
(c) (A) is True but (R) is False.
(d) (A) is False but (R) is True.
Ans: (d)
A glass tube partially filled with water represents a closed organ pipe because the water level acts as a closed end, creating a node, and the open end of the tube acts as an open end, creating an antinode. The open end corresponds to an antinode, and the closed end corresponds to a node.
The explanation for the answer is:
Assertion (A) is False: A glass tube partially filled with water is a closed organ pipe, not an open one. An open pipe would have two open ends.
Reason (R) is True: The open end of the glass tube will indeed correspond to an antinode and the end in contact with water will be a node, as that is the closed end.
Q2: The displacement of a traveling wave is given by y = C sin(2π / λ)(at − x) where t is time, x is distance, and λ is the wavelength, all in SI units. The frequency of the wave is: (NEET 2024)
(a) 2πλ / a
(b) 2πa / λ
(c) λ / a
(d) a / λ
Ans: (d)
The given displacement of a traveling wave is:
y = C sin( (2π / λ) (at − x) )
Here:
- C is the amplitude,
- t is time,
- x is distance,
- λ is the wavelength,
- a is a constant related to the velocity of the wave.
The general form of a traveling wave is:
y(x,t) = A sin(kx − ωt + φ)
Where:
- k = 2π / λ is the wave number,
- ω = 2πf is the angular frequency,
- f is the frequency.
From the equation, we can see that the wave is traveling with a velocity v = a.
This velocity is related to the wavelength and frequency by: v = λf
So, we can equate: a = λf
Solving for f, the frequency: f = a / λ
Correct Answer: (d) a / λ
2023
Q1: The ratio of frequencies of fundamental harmonic produced by an open pipe to that of closed pipe having the same length is [NEET 2023]
(a) 1 : 2
(b) 2 : 1
(c) 1 : 3
(d) 3 : 1
Ans: (b)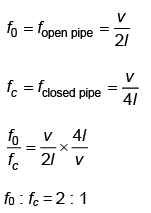
Q2: The 4th overtone of a closed organ pipe is the same as that of the 3rd overtone of an open pipe. The ratio of the length of the closed pipe to the length of the open pipe is: [NEET 2023]
(a) 8 : 9
(b) 9 : 7
(c) 9 : 8
(d) 7 : 9
Ans: (c)
Harmonics in a closed organ pipe:
For a closed organ pipe, the fundamental frequency is produced with a node at the closed end and an antinode at the open end. The harmonics are only odd-numbered (1st, 3rd, 5th, etc.).
- The 1st harmonic (fundamental) has the wavelength: λ₁ = 4L (where L is the length of the pipe).
- The 2nd harmonic is the 3rd overtone (and so on).
Harmonics in an open organ pipe:
For an open organ pipe, the fundamental frequency has antinodes at both ends. The harmonics are all integer multiples of the fundamental (1st, 2nd, 3rd, etc.).
- The 1st harmonic (fundamental) has the wavelength: λ₁ = 2L.
- The 2nd harmonic is the 1st overtone, the 3rd harmonic is the 2nd overtone, and so on.
Given:
- The 4th overtone of the closed pipe corresponds to the 3rd overtone of the open pipe.
- In a closed pipe, the 4th overtone corresponds to the 9th harmonic (because only odd harmonics are present).
- In an open pipe, the 3rd overtone corresponds to the 4th harmonic.
Now, let's use the fact that the frequency for both pipes should be the same for the given harmonics.
For a closed pipe (where only odd harmonics are present):
The 9th harmonic has a wavelength λ₉ = 4L/9.
For an open pipe:
The 4th harmonic has a wavelength λ₄ = 2L₁/4 = L₁/2.
Since the frequency is the same for both pipes, we set the wavelengths equal to each other:
λ₉ = λ₄
So, we have:
4L/9 = L₁/2
Solving for the ratio of the lengths:
L/L₁ = 9/8
Correct Answer: (c) 9 : 8
2022
Q1: If the initial tension on a stretched string is doubled, then the ratio of the initial and final speeds of a transverse wave along the string is [NEET 2022]
(a) 1:2
(b) 1:1
(c) √2:1
(d) 1:√2
Ans: (d)
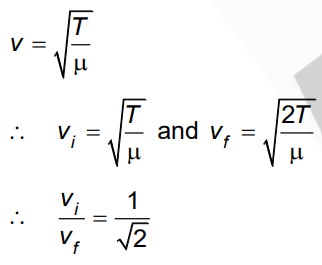
Q2: An organ pipe filled with a gas at 27∘C resonates at 400 Hz in its fundamental mode. If it is filled with the same gas at 90∘C, the resonance frequency at the same mode will be [NEET 2022]
(a) 512 Hz
(b) 480 Hz
(c) 440 Hz
(d) 484 Hz
Ans: (c)
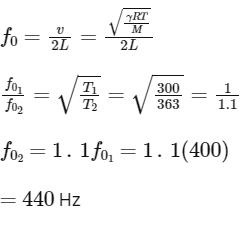
2020
Q1: In a guitar, two strings A and B made of same material are slightly out of tune and produce beats of frequency 6 Hz. When tension in B is slightly decreased, the beat frequency increases to 7 Hz. If the frequency of A is 530 Hz, the original frequency of B will be : [2020]
(a) 536 Hz
(b) 537 Hz
(c) 523 Hz
(d) 524 Hz
Ans: (d)
Frequency of A = fA = 530 Hz, fB = ?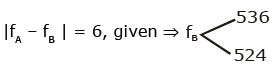
when Tension B ↓ then fB ↓, Beat Freq. ↑ to 7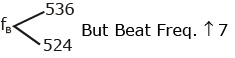
so if fB = 524 then Beat ↑ when fB ↓
So fB = 524 Hz
Q2: The phase difference between the displacement and acceleration of a particle in a simple harmonic motion is: [2020]
(a) π/2 rad
(b) zero
(c) π rad
(d) 3π/2 rad
Ans: (c)
for SHM acceleration and displacement both must have opposite direction
a = –ω2x ∴ phase diff. is π
∴ x = A sin (ωt), a = -Aω2sinωt
2018
Q1: A tuning fork is used to produce resonance in a glass tube. The length of the air column in this tube can be adjusted by a variable piston. At room temperature of 27°C two successive resonances are produced at 20 cm and 73 cm column length. If the frequency of the tuning fork is 320 Hz, the velocity of sound in air at 27°C is:- [2018]
(a) 330 m/s
(b) 339 m/s
(c) 350 m/s
(d) 300 m/s
Ans: (b)
Solution: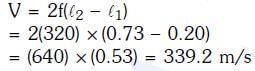
Q2: The fundamental frequency in an open organ pipe is equal to the third harmonic of a closed organ pipe. If the length of the closed organ pipe is 20cm, the length of the open organ pipe is:- [2018]
(a) 13.3 cm
(b) 8 cm
(c) 12.5 cm
(d) 16 cm
Ans: (a)
Solution: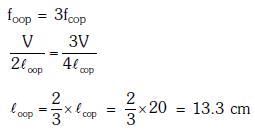
2017
Q1: The two nearest harmonics of a tube closed at one end and open at other end are 220 Hz and 260 Hz. What is the fundamental frequency of the system? [2017]
(a) 20 Hz
(b) 30 Hz
(c) 40 Hz
(d) 10 Hz
Ans: (a)
Solution:
Two successive frequencies of closed pipe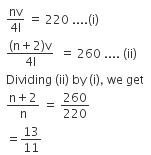
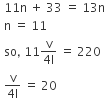
Q2: Two cars moving in opposite directions approach each other with speed of 22 m/s and 16.5 m/s respectively. The driver of the first car blows a horn having a a frequency 400 Hz. The frequency heard by the driver of the second car is [velocity of sound 340 m/s]:- [2017]
(a) 361 Hz
(b) 411 Hz
(c) 448 Hz
(d) 350 Hz
Ans: (c)
Solution: 
2016
Q1: A siren emitting a sound of frequency 800 Hz moves away from an observer towards a cliff at a speed of 15 ms-1. Then, the frequency of sound that the observer hears in the echo reflected from the cliff is : (Take velocity of sound in air = 330 ms-1) [2016]
(a) 885Hz
(b) 765 Hz
(c) 800 Hz
(d) 838 Hz
Ans: (d)
Solution: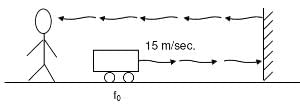

Since the observer and the wall are stationary so frequency of echo observed by the observer will also be 838 Hz.
Q2: An air column, closed at one end and open at the other, resonantes with a tuning fork when the smallest length of the column is 50 cm. The next larger length of the column resonating with the same tuning fork is: [2016]
(a) 200 cm
(b) 66.7 cm
(c) 100 cm
(d) 150 cm
Ans: (d)
Solution:
The smallest length of the air column is associated with the fundamental mode of vibration of the air column.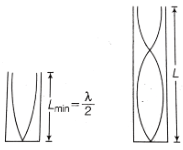
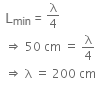
The next higher length of the air column is,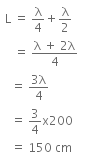
Q3: A uniform rope of length L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ1/λ2 is : [2016]
(a) 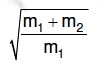
(b) 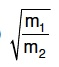
(c) 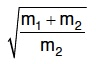
(d) 
Ans: (c)
Solution: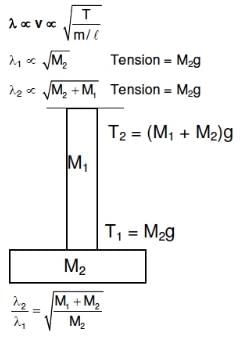
Q4: The second overtone of an open organ pipe has the same frequency as the first overtone of a closed pipe L metre long. The length of the open pipe will be [2016]
(a) L
(b) 2L
(c)L/2
(d) 4L
Ans: (b)
Second overtone of an open organ pipe

Q5: Three sound waves of equal amplitudes have frequencies (n − 1), n, (n + 1). They superimpose to give beats. The number of beats produced per second will be [2016]
(a) 1
(b) 4
(c) 3
(d) 2
Ans: (d)
(n – 1) and (n + 1) suppose to form frequency n
n and n will be at resonance
n – 1 and n produce 1 beat
n + 1 and n produce 1 beat
∴ Number of beats formed are ‘2’
2015
Q1: The fundamental frequency of a closed organ pipe of length 20 cm is equal to the second overtone of an organ pipe open at both the ends. The length of organ pipe open at both the ends is: [2015]
(a) 140 cm
(b) 80 cm
(c) 100 cm
(d) 120 cm
Ans: (d)
Solution:
For closed organ pipe fundamental frequency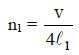
For open organ pipe fundamental frequency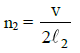
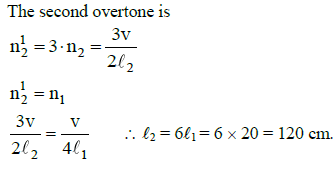
Q2: A string is stretched between fixed points separated by 75.0 cm. It is observed to have resonant frequencies of 420 Hz and 315 Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this string is [2015]
(a) 10.5 Hz
(b) 105 Hz
(c) 155 Hz
(d) 205 Hz
Ans: (b)
In a stretched string all multiples of frequencies can be obtained i.e., if fundamental frequency is n then higher frequencies will be 2n, 3n, 4n
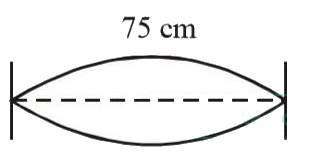
So, the difference between any two successive frequencies will be 'n'
According to question, n = 420 – 315 = 105Hz
So the lowest frequency of the string is 105 Hz.
Q3: 4.0 g of a gas occupies 22.4 litres at NTP. The specific heat capacity of the gas at constant volume is 5.0 J K
(Take gas constant R
(a) 7.0 J K
(b) 8.5 J K
(c) 8.0 J K
(d) 7.5 J K
Ans: (c)
Molar mass of the gas = 4g/mol
Speed of sound
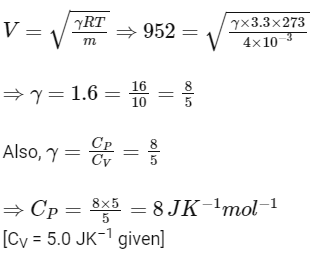
Q4: A source of sound S emitting waves of frequency 100 Hz and an observer O are located at some distance from each other. The source is moving with a speed of 19.4 m s
 (a) 106 Hz
(a) 106 Hz
(b) 97 Hz
(c)100 Hz
(d) 103 Hz
Ans: (d)
Here, original frequency of sound, f0 = 100 Hz
Speed of source Vs = 19.4 cos 60° = 9.7
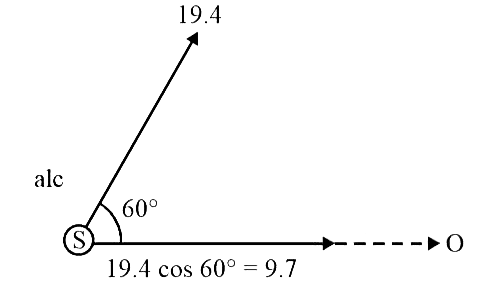
From Doppler's formula
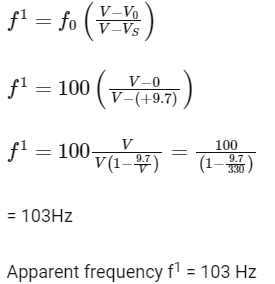
2014
Q1: If n1, n2, and n3 are the fundamental frequencies of three segments into which a string is divided, then the original fundamental frequency n of the string is given by: [2014]
(a) 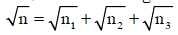
(b) n = n1 + n2 + n3
(c) 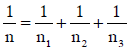
(d) 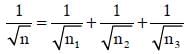
Ans: (c)
Solution: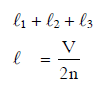
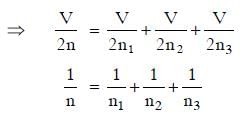
Q2: The number of possible natural oscillations of air column in a pipe closed at one end of length 85 cm whose frequencies lie below 1250 Hz are : (velocity of sound = 340 ms−1) [2014]
(a) 7
(b) 6
(c) 4
(d) 5
Ans: (b)
Solution: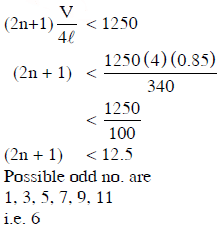
Q3: A speeding motorcyclist sees traffic jam ahead of him. He slows down to 36 km/hour. He finds that traffic has eased and a car moving ahead of him at 18 km/hour is honking at a frequency of 1392 Hz. If the speed of sound is 343 m/s, the frequency of the honk as heard by him will be: [2014]
(a) 1412 Hz
(b) 1454 Hz
(c) 1332 Hz
(d) 1372 Hz
Ans: (a)
Solution: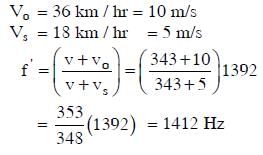
There is no Question for NEET 2021
|
94 videos|367 docs|98 tests
|
FAQs on NEET Previous Year Questions (2014-2025): Waves - Physics Class 11
| 1. What is the difference between transverse and longitudinal waves? |  |
| 2. How does frequency affect the properties of a wave? |  |
| 3. What is the relationship between wavelength and wave speed? |  |
| 4. How does amplitude impact the energy of a wave? |  |
| 5. How does the medium through which a wave travels affect its speed? |  |






















