JEE Main Previous Year Questions (2016- 2024): Work, Energy and Power | Physics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
Q 1. A particle (m = 1 kg) slides down a frictionless track (AOC) starting from rest at a point A (height 2 m). After reaching C, the particle continues to move freely in air as a projectile. When it reaches its highest point P (height 1 m), the kinetic energy of the particle (in J) is (Figure drawn is schematic and not to scale; take g = 10 m/s2) ______. [2020]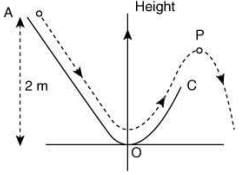
Ans: 10
Solution:
Given that m = 1 kg, g = 10 m/s2 , h1 = 2 m and h2 = 1 m.
According to law of conservation of energy, we have
Energy at point A = Energy at point P
⇒ (Potential energy + Kinetic energy)A = (Potential energy + Kinetic energy)P
⇒ mgh1 + K1 + mgh2 + K2
Since, K1 = 0. So,
2mg + 0 = mg + K2
⇒ K2 = mg
= 1 x 10 = 10 J
Q 2. An elevator in a building can carry a maximum of 10 persons, with the average mass of each person being 68 kg. The mass of the elevator itself is 920 kg and it moves with a constant speed of 3 m/s. The frictional force opposing the motion is 6000 N. If the elevator is moving up with its full capacity, the power delivered by the motor to the elevator (g = 10 m/s2 ) must be at least
(1) 56300 W
(2) 62360 W
(3) 48000 W
(4) 66000 W
Ans: (4)
Solution:
Given that
Capacity of elevator, C = 10 persons
Average mass of each person, mp = 68 kg
Mass of elevator, me = 920 kg
Speed of elevator, v = 3 m/s
Frictional force, f = 600 N
Force acting on motor is given by,
F = mtotal x g + f
= ( 10 x 68 + 920) x 10 + 6000
=16000 + 6000
= 22000
So, power delivered by motor is P = F x v
= 22000 x 3 = 66000 W
Therefore, power delivered by the motor to the elevator must be at least 66000 W.
Q 3. A body A, of mass m = 0.1 kg has an initial velocity of 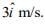 It collides elastically with another body, B of the same mass which has an initial velocity of
It collides elastically with another body, B of the same mass which has an initial velocity of 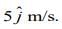 After collision, A moves with a velocity
After collision, A moves with a velocity 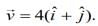 The energy of B after collision is written as (x/10) J. The value of x is ______.
The energy of B after collision is written as (x/10) J. The value of x is ______.
Ans: 1
Solution:
Given that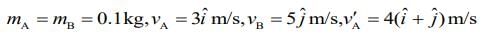
Since, collision is elastic so by the conservation of linear momentum
Initial momentum = Final momentum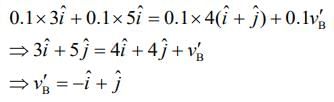
Kinetic energy of B after collision is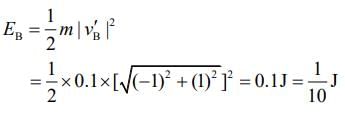
Therefore, x = 1
Q 4. A particle of mass m is dropped from a height h above the ground. At the same time, another particle of the same mass is thrown vertically upwards from the ground with a speed of 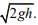 If they collide head-on completely inelastically, the time for the combined mass to reach the ground, in units of
If they collide head-on completely inelastically, the time for the combined mass to reach the ground, in units of 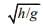 is [2020]
is [2020]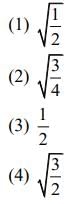
Ans: (4)
Solution:
Given that
mA = mB = m, v0,A = v0,B = 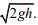
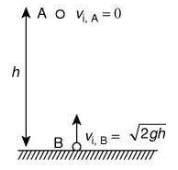
Time for collision is given by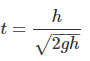
velocity before collision is
vi,A = gt, vi,B = V0,B - gt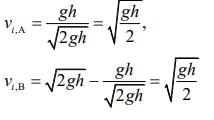
⇒ vi,A = -vi,B
From conservation of momentum, we have
mAvi.A + mBvi,B = mAvf,A + mBvf,B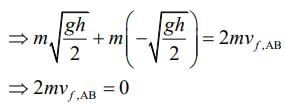
So, height from ground is given by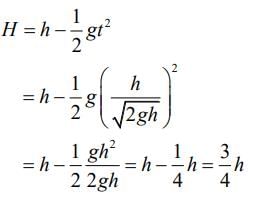
Q 5. Consider a force 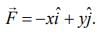 The work done (in J) by this force in moving a particle from point A(1, 0) to B(0, 1) along the line segment given in the fiigure is (all quantities are in SI units) [2020]
The work done (in J) by this force in moving a particle from point A(1, 0) to B(0, 1) along the line segment given in the fiigure is (all quantities are in SI units) [2020]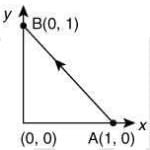
(1) 2
(2) 1/2
(3) 1
(4) 3/2
Ans: (3)
Solution:
Given that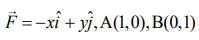
Work done by the force is given by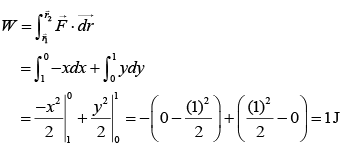
Q 6. Two particles of equal mass m have respective initial velocities 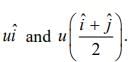 They collide completely inelastically. The energy lost in the process is [2020]
They collide completely inelastically. The energy lost in the process is [2020]
(1) 1/3 mμ2
(2) 1/8 mμ2
(3) 3/4 mμ2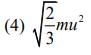
Ans: (2)
Solution:
Given that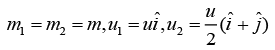
Since collision is inelastic only momentum is conserved. So,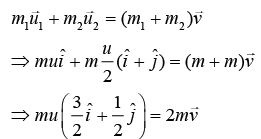
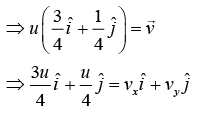
Change in kinetic energy is given by
ΔK = Kf - Ki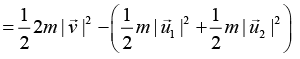
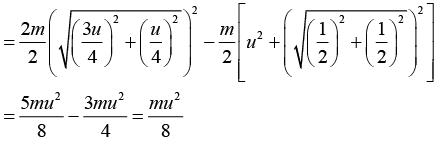
Q 7. A particle of mass m is projected with a speed u from the ground at an angle θ =π/3 w.r.t. horizontal (x-axis). When it has reached its maximum height, it collides completely inealstically with another particle of the same mass and velocity 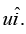 . The horizontal distance covered by the combined mass before reaching the ground is [2020]
. The horizontal distance covered by the combined mass before reaching the ground is [2020]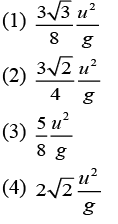
Ans: (1)
Solution:
Given that initial speed u, angle of projection from ground θ = π/3
Speed of particle at height point is given by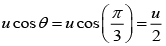
Applying conservation of momentum, we have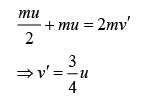
Time of flight after collision is given by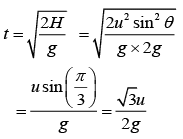
Range after collision is given by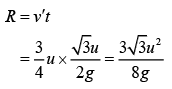
Q 8. A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initially at rest in its equilibrium position. If now the block is pulled with a constant force F, the maximum speed of the block is (2019)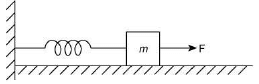
(1) 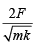
(2) 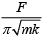
(3) 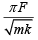
(4) 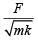
Ans: (4)
Solution:
The maximum speed of block is at mean position F = kx (equilibrium)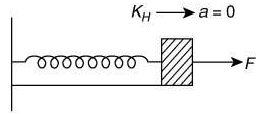
According to work energy theorem,
Work done by external force + work done by spring = Change in kinetic energy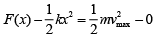
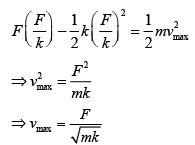
Q 9. Three blocks A, B and C are lying on a smooth horizontal surface, as shown in the figure. A and B have equal masses 'm', while C has mass 'M'. Block A is given an initial speed v toward B due to which it collides with B perfectly inelastically. The combined mass collides with C, also perfectly inelastically and 5/6th of the initial kinetic energy is lost in whole process. What is value of M/m? (2019)
(1) 5
(2) 2
(3) 4
(4) 3
Ans: (3)
Solution:
From the linear momentum, we have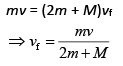
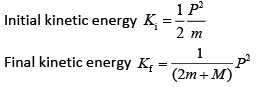
Now, according to the question,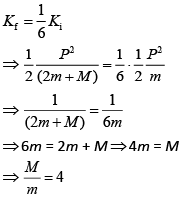
Q 10. A force acts on a 2 kg object so that its position is given as a function of time as x = 3t2 + 5. What is the work done by this force in first 5 s? (2019)
(1) 850 J
(2) 950 J
(3) 875 J
(4) 900 J
Ans: (4)
Solution:
The position of object as a function of time is given by
x = 3t2 + 5 -----(1)
We know that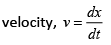
Differentiating w.r.t. Eq. (1) becomes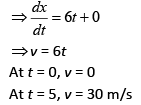
Therefore, work done by the force = change in K.E.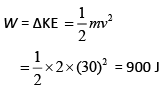
Q 11. A block of mass m is kept on a platform which starts from rest with constant acceleration g/2 upward, as shown in the figure. Work done by normal reaction on block in time t is (2019)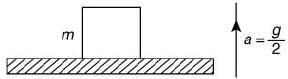
(1) 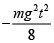
(2) 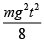
(3) 0
(4) 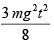
Ans: (4)
Solution:
According to the Newton second law
F = ma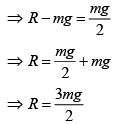
Work done is
Q 12. A piece of wood of mass 0.03 kg is dropped from the top of a 100 m height building. At the same time, a bullet of mass 0.02 kg is fired vertically upward, with a velocity 100 m/s, from the ground. The bullet gets embedded in the wood. Then the maximum height to which the combined system reaches above the top of the building before falling below is (g = 10 m/s2) (2019)
(1) 20 m
(2) 30 m
(3) 40 m
(4) 10 m
Ans: (3)
Solution:
Bullet will collide with piece of wood at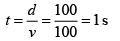
Velocity of piece of wood u = 0 + 10 × 1 = 10 m/s
Velocity of bullet v = 100 – 10 = 90 m/s
From conservation of linear momentum,
−(0.02) (1v) + (0.02) (9v) = (0.05)
⇒ 150 = 5v
⇒ v = 30 m/s
Maximum height reached by body is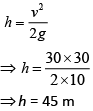
At time of collision system is h distance below top of tower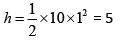
Therefore, height above tower = 45 – 5 = 40 m
Q 13. A particle which is experiencing a force, given by 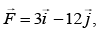 undergoes a displacement of
undergoes a displacement of 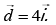 If the particle had a kinetic energy of 3 J at the beginning of the displacement, what is its kinetic energy at the end of the displacement? (2019)
If the particle had a kinetic energy of 3 J at the beginning of the displacement, what is its kinetic energy at the end of the displacement? (2019)
(1) 9 J
(2) 12 J
(3) 10 J
(4) 15 J
Ans: (4)
Solution: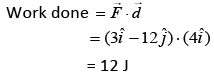
According to work-energy theorem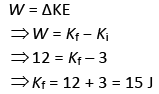
Q 14. A body of mass 1 kg falls freely from a height of 100 m on a platform of mass 3 kg which is mounted on a spring having spring constant k = 1.25 × 106 N/m. The body sticks to the platform and the spring’s maximum compression is found to be x. Given that g = 10 m/s2, the value of x will be close to (2019)
(1) 8 cm
(2) 4 cm
(3) 80 cm
(4) 40 cm
Ans: None of the above (*)
* None of the options is correct
Solution:
Initial compression is mg = kx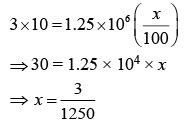
Velocity of 1 kg block just before it collides with 3 kg block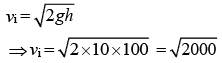
Applying momentum conversation just before and just after collision, we have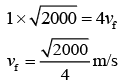
Now, applying work-energy theorem,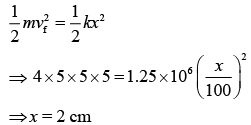
Q 15. An alpha-particle of mass m suffers one-dimensional elastic collision with a nucleus at rest of unknown mass. It is scattered directly backward losing, 64% of its initial kinetic energy. The mass of the nucleus is (2019)
(1) 2m
(2) 3.5m
(3) 1.5m
(4) 4m
Ans: (4)
Solution:
Applying law of conservation of momentum before collision,
mu1 + 0 = −mv1 + Mv2
⇒ mu1 = −mv1 + Mv2 (1)
Since, α-particle is scattered in backward thus, losing 64% of initial energy.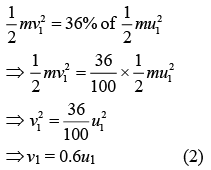
Now, coefficient of restitution
thus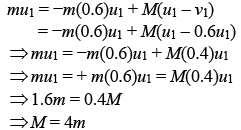
Q 16. A particle is moving in a circular path of radius 'a' under the action of an attractive potential 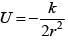 Its total energy is: (2018)
Its total energy is: (2018)
(1) 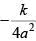
(2) 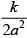
(3) Zero
(4) 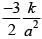
Ans: (3)
Solution:
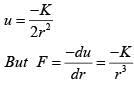
‘ – ‘ sign of force implies attractive force So,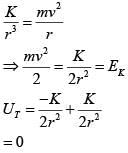
Q 17. In a collinear collision, a particle with an initial speed ν0 strikes a stationary particle of the same mass. If the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after collision, is: (2018)
(1) 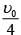
(2) 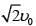
(3) 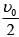
(4) 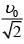
Ans: (2)
Solution:
By conservation of linear momentum,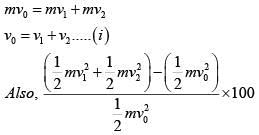
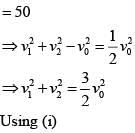
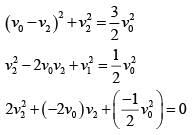
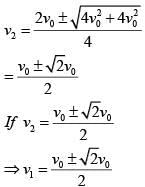
So relative velocity :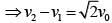
Hence the Solution is Option (2)
Q 18. A particle is moving with a uniform speed in a circular orbit of radius 'R' in a central force inversely proportional to the nth power of R. If the period of rotation of the particle is T, then: (2018)
(1) Tα R3/2 for any n.
(2) 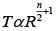
(3) Tα R(n+1)/2
(4) Tα Rn/2
Ans: (3)
Solution:
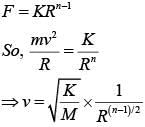
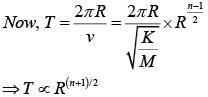
Q 19. A body of mass m starts moving from rest along x-axis so that its velocity varies as v = a√s where a is a constant and s is the distance covered by the body. The total work done by all the forces acting on the body in the first 't' seconds after the start of the motion is: (2018)
(1) (8) ma4t2
(2) (1/4) ma4t2
(3) (4) ma4t2
(4) (1/8) ma4t2
Ans: (4)
Solution: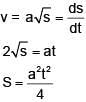
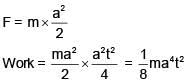
Q 20. Two particles of the same mass m are moving in circular orbits because of force given by 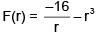 . The first particle is at distance r = 1 and the second at r = 4. The best estimate for the ratio of kinetic energies of the first and the second particle is closest to (2018)
. The first particle is at distance r = 1 and the second at r = 4. The best estimate for the ratio of kinetic energies of the first and the second particle is closest to (2018)
(1) 3 × 10–3
(2) 6 × 102
(3) 6 × 10–2
(4) 10–1
Ans: (3)
Solution: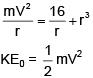
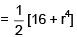
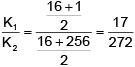
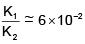
Q 21. A body of mass m = 10–2 kg is moving in a medium and experiences a frictional force F = –kv2. Its initial speed is v0 = 10 ms–1. If after 10 s, its energy is 1/8 mv02, the value of k will be (2017)
(1) 10–4 kg m–1
(2) 10-1 kg m–1 s-1
(3) 10-3 kg m-1
(4) 10-3 kg s-1
Ans: (1)
Solution: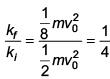
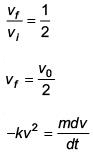

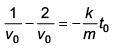
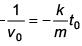
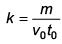
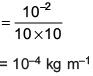
Q 22. A time dependent force F = 6t acts on a particle of mass 1 kg. If the particle starts from rest, the work done by the force during the first 1 second will be (2017)
(1) 9 J
(2) 18 J
(3) 4.5 J
(4) 22 J
Ans: (3)
Solution: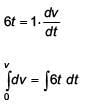
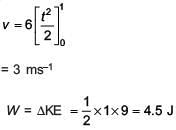
Q 23. An object is dropped from a height h from the ground. Every time it hits the ground it loses 50% of its kinetic energy. The total distance covered in t → ∞ is - (2017)
(1) 3h
(2) ∞
(3) 5/3h
(4) 8/3h
Ans: (1)
Solution: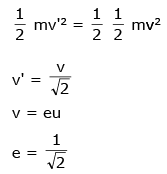
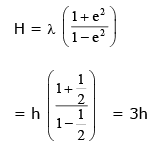
Q 24. Two particles A and B of equal mass M are moving with the same speed u as shown in the figure. They collide completely inelastically and move as a single particle C. The angle q that the path of C makes with the X-axis is given by- (2017)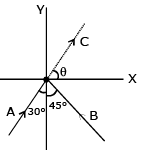
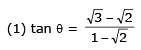
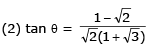

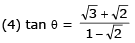
Ans: (4)
Solution:
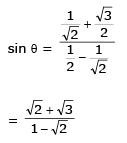
Q 25. A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up? Fat supplies 3.8 x 107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. (Take g = 9.8 ms-2): (2016)
A: 2.45 x 10-3 kg
B: 6.45 x 10-3 kg
C: 9.89 x 10-3 kg
D: 12.89 x 10-3 kg
Ans: D
Solution:
0.2 x 3.8 x 107 x m = 10 x g x 1 x 1000
m = 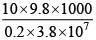
= 1.289 x 10-2 Kg
= 12.89 x 10-3 Kg
Q 26. Velocity- time graph for a body of mass 10 kg is shown in figure. Work- done on the body in first two seconds of the motion is: (2016)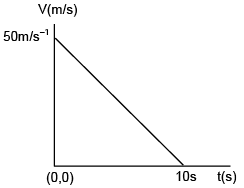
(1) 12000 J
(2) –12000 J
(3) –4500 J
(4) –9300 J
Ans: (3)
Solution: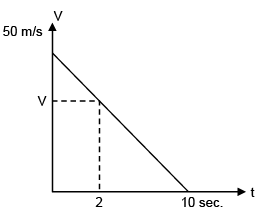
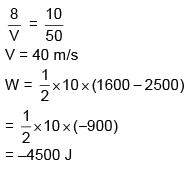
Q 27. A particle of mass m is acted upon by a force F given by the empirical law 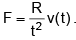 If this law is to be tested experimentally by observing the motion starting from rest, the best way is to plot: (2016)
If this law is to be tested experimentally by observing the motion starting from rest, the best way is to plot: (2016)
(1) log v(t) against t
(2) v(t) against t2
(3) log v(t) against 1/t2
(4) log v(t) against 1/t
Ans: (4)
Solution: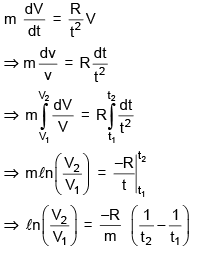
logV vs 1/t will be a st. line curve.
Q 28. A particle of mass M is moving in a circle of fixed radius R in such a way that its centripetal acceleration at time t is given by n2 R t2 where n is a constant. The power delivered to the particle by the force acting on it, is: (2016)
(1) M n R2 t2
(2) 1/2 Mn2R2t2
(3) Mn2R2t
(4) MnR2t
Ans: (3)
Solution: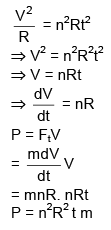
|
199 videos|422 docs|281 tests
|























