JEE Main Previous Year Questions (2016- 2025): Inverse Trigonometric Functions | Mathematics for GRE Paper II PDF Download
Q.1.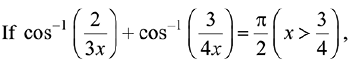 then x is equal to: (2019)
then x is equal to: (2019)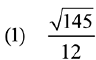
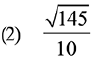
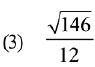
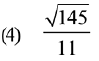
Ans. (1)
Solution.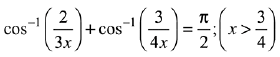
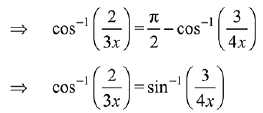

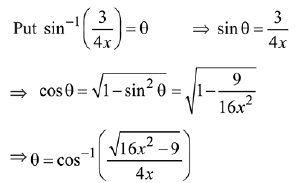
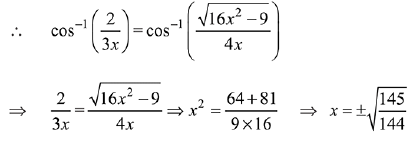
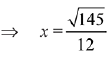
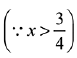
Q.2. If x = sin-1 (sin 10) and y = cos-1 (cos 10), then y - x is equal to: (2019)
(1) 0
(2) 10
(3) 7 π
(4) π
Ans. (4)
Solution.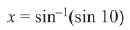
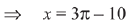
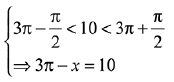
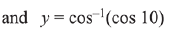
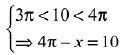

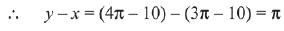
Q.3. 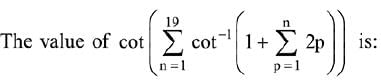 (2019)
(2019)
(1) 21/19
(2) 19/21
(3) 22/23
(4) 23/22
Ans. (1)
Solution.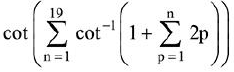
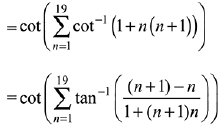
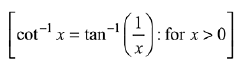
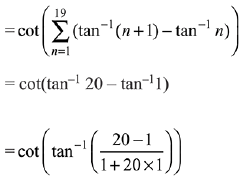
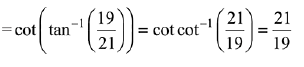
Q.4. All x-satisfying the inequality (cot-1 x)2 - 7(cot-1x)+ 10 > 0, lie in the interval: (2019)
(1) (-∞, cot 5) ∪ (cot 4, cot 2)
(2) (cot 2, ∞)
(3) (-∞, cot 5) ∪ (cot 2, ∞)
(4) (cot 5, cot 4)
Ans. (2)
Solution.
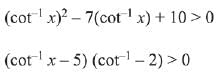
⇒ ...(1)
...(1)
But cot-1 x lies in (0, π)
Now, from equation (1)
cot-1x ∈ (0, 2)
Now, it is clear from the graph
x ∈ (cot 2, ∞)
Q.5. Considering only the principal values of inverse functions, the set 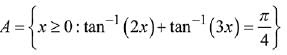 (2019)
(2019)
(1) contains two elements
(2) contains more than two elements
(3) is a singleton
(4) is an empty set
Ans. (3)
Solution.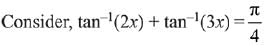
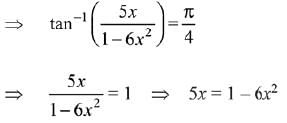
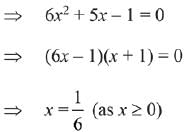
Therefore, A is a singleton set.
Q.6.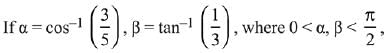 then α - β is equal to: (2019)
then α - β is equal to: (2019)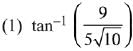
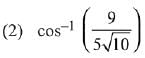
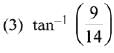
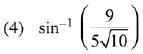
Ans. (4)
Solution.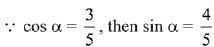
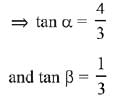
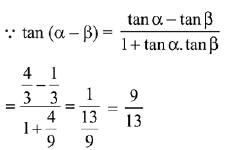
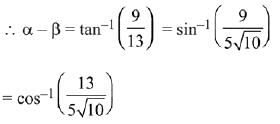
Q.7.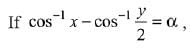 where -1 ≤ x ≤ 1, -2 ≤ y ≤ 2,
where -1 ≤ x ≤ 1, -2 ≤ y ≤ 2, 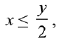 then for all x, y, 4x2 -4xy cosα +y2 is equal to: (2019)
then for all x, y, 4x2 -4xy cosα +y2 is equal to: (2019)
(1) 4 sin2α
(2) 2 sin2α
(3) 4 sin2α - 2x2y2
(d) 4 cos2 α + 2x2y2
Ans. (1)
Solution.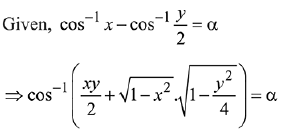
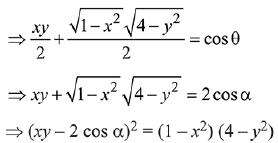
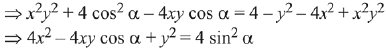
Q.8. The value of 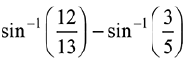 is equal to: (2019)
is equal to: (2019)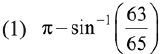
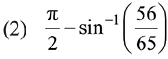
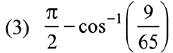
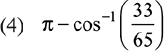
Ans. (2)
Solution.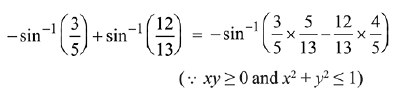
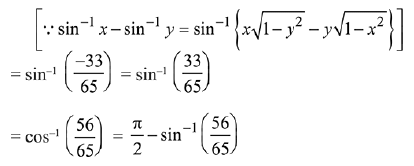
Q.9. If for x∈ 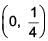 the derivative of tan-1
the derivative of tan-1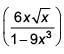 is √x × g(x) , then g(x) equals (2017)
is √x × g(x) , then g(x) equals (2017)
(1) 
(2) 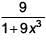
(3) 
(4)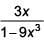
Ans. (2)
Solution.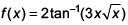
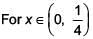
⇒ 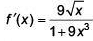
⇒ 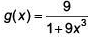
Q.10. The value of is equal to: (2017)
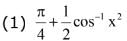
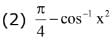

Ans. (1)
Solution.
x2 = cos2θ ; θ = 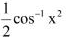
= 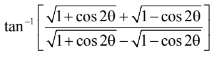
= 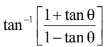
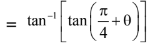
=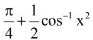
Q.11. A value of x satisfying the equation sin[cot-1(1+x)]=cos[tan-1x], is: (2017)
(1) 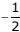
(2) 0
(3) -1
(4) 1/2
Ans. (1)
Solution.
Given that sin[cot-1 (x+1)] = cos (tan-1x) ......(i)
We know that,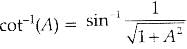
Here, A = x + 1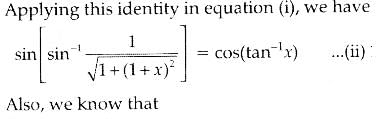
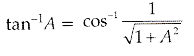
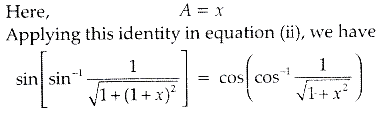
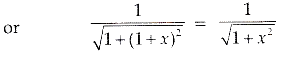
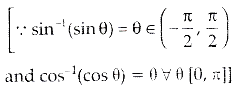
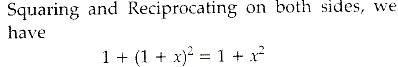
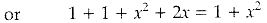
or 1 + 2x = 0
or 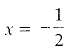
Q.12. Consider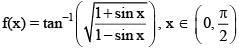
A normal to y = f(x) at x = π/6 also passes through the point: (2016)
(1) (0, 0)
(2) (0, 2π/3)
(3) (π/6, 0)
(4) (π/4, 0)
Ans. (2)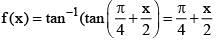
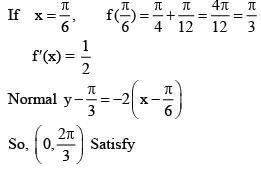
|
237 videos|197 docs|150 tests
|
















