NCERT Exemplar: Electromagnetic Waves | Physics for JEE Main & Advanced PDF Download
MULTIPLE CHOICE QUESTIONS I
Q.1. One requires 11eV of energy to dissociate a carbon monoxide molecule into carbon and oxygen atoms. The minimum frequency of the appropriate electromagnetic radiation to achieve the dissociation lies in
(a) Visible region.
(b) Infrared region.
(c) Ultraviolet region.
(d) Microwave region.
Ans. (c)
Solution.
E = 11 eV = 11×1.6×10-19 J
h = 6.62×10-34 J-S
E = hf
f = E/h =
= 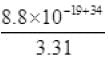
= 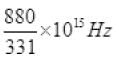
= 2.65 x 1015 Hz
This frequency radiation belongs to the ultraviolet region.
Q.2. A linearly polarized electromagnetic wave given as is incident normally on a perfectly reflecting infinite wall at z = a. Assuming that the material of the wall is optically inactive, the reflected wave will be given as
is incident normally on a perfectly reflecting infinite wall at z = a. Assuming that the material of the wall is optically inactive, the reflected wave will be given as
(a) Er = – Eo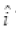 cos (kz-ωt)
cos (kz-ωt)
(b) Er = Eo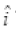 cos (kz +ωt)
cos (kz +ωt)
(c) Er = - Eo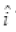 cos (kz+ωt)
cos (kz+ωt)
(d) Er = Eo sin(kz-ωt)
sin(kz-ωt)
Ans. (b)
Solution.
Key concept: When a wave is reflected from a denser medium or perfectly reflecting wall made with optically inactive material, then the type of wave doesn’t change but only its phase changes by 180° or π radian.
Q.3. Light with an energy flux of 20 W/cm2 falls on a non-reflecting surface at normal incidence. If the surface has an area of 30 cm2. the total momentum delivered (for complete absorption) during 30 minutes is
(a) 36 × 10–5 kg m/s.
(b) 36 × 10–4 kg m/s.
(c) 108 × 104 kg m/s.
(d) 1.08 × 107 kg m/s.
Ans. (b)
Solution.
Energy flux= ϕ =20 W/cm2
Area A= 30cm2, time t = 30×60 sec
U= total energy falling t sec= Energy flux * Area * time = ϕ At
U= 20×30×30×60 J
Momentum of the incident light =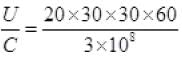
= 36×10-4 kg ms-1
As no reflection from the surface and for complete absorption so momentum of reflected radiation is zero.
Momentum delivered to surface= Change in momentum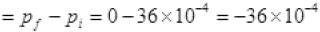 kg m/s
kg m/s
(-) sign shows the direction of momentum.
Q.4. The electric field intensity produced by the radiations coming from 100 W bulb at a 3 m distance is E. The electric field intensity produced by the radiations coming from 50 W bulb at the same distance is
(a) E/2
(b) 2E
(c) E/√2
(d) √2E
Ans. (c)
Solution.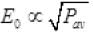
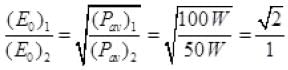
∴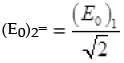
Q.5. If E and B represent electric and magnetic field vectors of the electromagnetic wave, the direction of propagation of electromagnetic wave is along
(a) E.
(b) B.
(c) B × E.
(d) E × B .
Ans.(d)
Solution.
A changing electric field produces a changing magnetic field and vice versa which gives rise to a transverse wave known as electromagnetic wave. The time varying electric and magnetic field are mutually perpendicular to each other and also perpendicular to the direction of propagation of this wave. The electric vector is responsible for the optical effects of an EM wave and is called the light vector.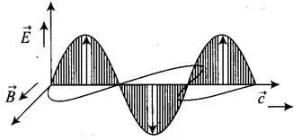 The direction of propagation of electromagnetic w ave is perpendicular to both electric field vector (
The direction of propagation of electromagnetic w ave is perpendicular to both electric field vector ( ) and
) and magnetic field vector B, i.e., in the direction of
magnetic field vector B, i.e., in the direction of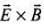 .
.
Here, electromagnetic wave is along the z-direction which is given by the cross product o f E and B.
Q.6. The ratio of contributions made by the electric field and magnetic field components to the intensity of an EM wave is
(a) c : 1
(b) c2 : 1
(c) 1 : 1
(d) √c :1
Ans. (c)
Solution.
The intensity of electromagnetic wave is given by, I = Uavc, where Uav =Average energy and c = speed of light
Intensity in relation with electric field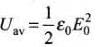
Intensity relation with magnetic field 
Now taking the intensity in terms of electric field,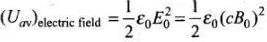
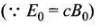
But,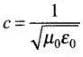
∴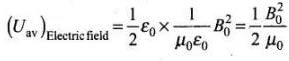
= (Uav)magnetic field
Q.7. An EM wave radiates outwards from a dipole antenna, with E0 as the amplitude of its electric field vector. The electric field E0 which transports significant energy from the source falls off as
(a) 1/r3
(b) 1/r2
(c) 1/r
(d) Remains constant.
Ans. (c)
Solution.
As we know that electromagnetic waves are radiated from dipole antenna and radiated energy E ∝ 1/r
Q.8. An electromagnetic wave travels in vacuum along z direction: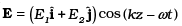 .
.
Choose the correct options from the following:
(a) The associated magnetic field is given as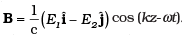
(b) The associated magnetic field is given as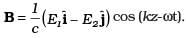
(c) The given electromagnetic field is circularly polarised.
(d) The given electromagnetic wave is plane polarised.
Ans. (a) and (d)
Solution.
Here, in electromagnetic wave, the electric field vector is given as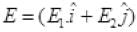 cos(kz-ωt). In electromagnetic wave the associated magnetic field Vector
cos(kz-ωt). In electromagnetic wave the associated magnetic field Vector 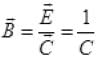 (E1i+E2j)cos(kz-ωt) verify option (a) and (b) as
(E1i+E2j)cos(kz-ωt) verify option (a) and (b) as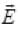 and
and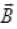 are long X- and Y-axis respectively so the direction of propagation is Z-axis and E.M. wave is plane polarized along X and Y direction
are long X- and Y-axis respectively so the direction of propagation is Z-axis and E.M. wave is plane polarized along X and Y direction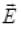 and
and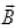 respectively verifies option (d).
respectively verifies option (d).
Q.9. An electromagnetic wave traveling along z-axis is given as E = E0 cos (kz - ωt).
Choose the correct options from the following:
(a) The associated magnetic field is given as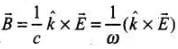
(b) The electromagnetic field can be written in terms of the associated magnetic field as 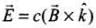
(c) kˆ.E = 0, kˆ.B= 0.
(d) kˆ×E= 0, kˆ× B = 0.
Ans. (a), (b) and (c)
Solution.
(a) The direction of propagation of an electromagnetic wave is always along the direction of vector product E x B. Refer to Figure.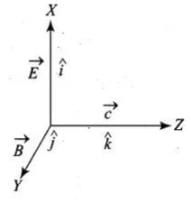
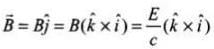

(b)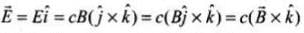
(c)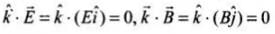
(d)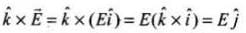
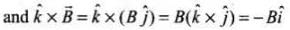
Q.10. A plane electromagnetic wave propagating along x direction can have the following pairs of E and B
(a) Ex, By.
(b) Ey, Bz.
(c) Bx, Ey.
(d) Ez, By.
Ans. (b) and (d)
Solution.
As the EM wave is plane polarized and its propagation is in +X direction. So direction of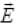 and
and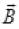 will be in either Y and Z direction or Z and Y direction. So verifies answers (b) and (d).
will be in either Y and Z direction or Z and Y direction. So verifies answers (b) and (d).
Q.11. A charged particle oscillates about its mean equilibrium position with a frequency of 109 Hz. The electromagnetic waves produced:
(a) Will have frequency of 109 Hz.
(b) Will have frequency of 2 × 109 Hz.
(c) Will have a wavelength of 0.3 m.
(d) Fall in the region of radio waves.
Ans. (a) (c) and (d)
Solution.
Vibrating particle produces electric and magnetic field, so will produce an E.M. wave of same frequency 109 Hz verifies answer (a).
∵ V= 109 Hz, c=3×108 m/s
So,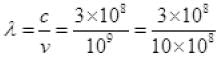
= 0.3 m
verifies answer (c)
As the range of radio waves are between 10 Hz to 1012 Hz and 109 Hz lies between this range verifies answer (d).
Q.12. The source of electromagnetic waves can be a charge
(a) Moving with a constant velocity.
(b) Moving in a circular orbit.
(c) At rest.
(d) Falling in an electric field.
Ans. (b, d)
Solution.
Key concept:
- An electromagnetic wave can be produced by accelerated or oscillating charge.
- An oscillating charge is accelerating continuously, it will radiate electromagnetic waves continuously.
- Electromagnetic waves are also produced when fast moving electrons are suddenly stopped by a metal target of high atomic number.
Here, in option (b) charge is moving in a circular orbit.
In circular motion, the direction of the motion of charge is changing continuously, thus it is an accelerated motion and this option is correct.
In option (d), the charge is falling in electric field. If a charged particle is moving in electric field it experiences a force or we can say it accelerates. We know an accelerating charge particle radiates electromagnetic waves. Hence option (d) is also correct.
Also, we know that a charge starts accelerating when it falls in an electric field.
Important points:
- In an atom an electron is circulating around the nucleus in a stable orbit, although accelerating does not emit electromagnetic waves; it does so only when it jumps from a higher energy orbit to a lower energy orbit.
- A simple LC oscillator and energy source can produce waves of desired frequency.
Q.13. An EM wave of intensity I falls on a surface kept in vacuum and exerts radiation pressure p on it. Which of the following are true?
(a) Radiation pressure is I/c if the wave is totally absorbed.
(b) Radiation pressure is I/c if the wave is totally reflected.
(c) Radiation pressure is 2I/c if the wave is totally reflected.
(d) Radiation pressure is in the range I/c < p < 2I/c for real surfaces.
Ans. (a) (c) and (d)
Solution.
Radiation pressure is the force exerted by particles (dual nature of particle) on unit area, due to the change in momentum of radiated particles per unit area per sec = 1/c.
I= intensity of radiation
C= velocity of radiation
Radiations are absorbed, so momentum per unit area per second verify the answer (a).
When radiation is reflected back, the momentum becomes double as in earlier case, so discards answer (b) and verifies answer (c).
So variation of radiation pressure p comes between the range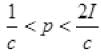 verifies answer (d).
verifies answer (d).
VERY SHORT ANSWER TYPE QUESTIONS
Q.14. Why is the orientation of the portable radio with respect to broadcasting station important?
Ans. Transmitted carrier wave signals are plane polarized and if the intensity of signal is poor then receiving antenna of radio must be parallel to the component of either electric or magnetic field. Because energy is only due to amplitudes of electric and magnetic components in EM wave, magnitude of amplitude is in particular direction perpendicular to each other and perpendicular to wave propagation.
Q.15. Why does microwave oven heats up a food item containing water molecules most efficiently?
Ans. In Microwave oven, molecules of food item starts to vibrate by driven force due to microwaves with the frequency of microwave. But the natural frequency of water molecules matches with microwave frequency which causes resonance (more amplitude) which further causes increase in temperature.
Q.16. The charge on a parallel plate capacitor varies as q = q0cos 2πνt. The plates are very large and close together (area = A, separation = d). Neglecting the edge effects, find the displacement current through the capacitor?
Ans. The displacement current Id in capacitor is Id=IC
= dq/dt, where q = q0 cos(2πvt) (Given)
Id=IC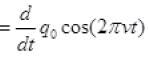
Id = -q0 2πv sin πvt
Id=-2πvq0πvt)
Q.17. A variable frequency a.c source is connected to a capacitor. How will the displacement current change with decrease in frequency?
Ans. As we know that Xc = 1/2πvC and I = V/Xc
So reactance of capacitor increases on decreasing frequency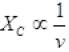
So I = 2πv CV
As reactance of capacitor increases, the current by Ohm’s law will decrease.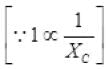
So the displacement current decreases frequency decreases when the conduction current is equal to displacement current.
Q.18. The magnetic field of a beam emerging from a filter facing a floodlight is given by B0 = 12 × 10–8sin (1.20 × 107z – 3.60 × 1015 t)T. What is the average intensity of the beam?
Ans. The standard equation of magnetic field can be expressed as B = B0 sinωt.
We are given equation
B = 12 x 10-8 sin (120 x 107z - 3.60 x 101/5t)T .......... (i)
On comparing this equation with standard equation, we get
B0= 12 x 10-8 T
The average intensity of the beam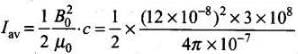
= 1.71 W/m2
Q.19. Poynting vectors S is defined as a vector whose magnitude is equal to the wave intensity and whose direction is along the direction of wave propagation. Mathematically, it is given by 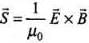 . Show the nature of S vs t graph.
. Show the nature of S vs t graph.
Ans. In an electromagnetic waves, let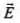 be varying along y-axis,
be varying along y-axis,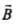 is along z-axis and propagation o f wave be along x-axis. Then
is along z-axis and propagation o f wave be along x-axis. Then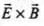 will tell the direction of propagation of energy flow in electromagnetic wave, along x-axis.
will tell the direction of propagation of energy flow in electromagnetic wave, along x-axis.
Let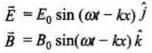

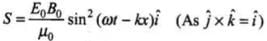
Since sin2(ωt - kx) is never negative,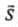 (x, t) always points in the positive A'-direction, i.e, in the direction of wave propagation.
(x, t) always points in the positive A'-direction, i.e, in the direction of wave propagation.
The variation of |S| with time T will be as given in the figure below: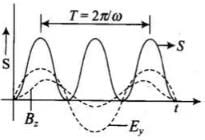
Q.20. Professor C.V Raman surprised his students by suspending freely a tiny light ball in a transparent vacuum chamber by shining a laser beam on it. Which property of EM waves was he exhibiting? Give one more example of this property.
Ans. The properties of an electromagnetic wave is same as other waves. Like other wave an electromagnetic wave also carries energy and momentum. Since, it carries momentum, an electromagnetic wave also exerts pressure called radiation pressure. This property of electromagnetic waves helped professor C V Raman surprised his students by suspending freely a tiny light ball in a transparent vacuum chamber by shining a laser beam on it.
SHORT ANSWER TYPE QUESTIONS
Q.21. Show that the magnetic field B at a point in between the plates of a parallel-plate capacitor during charging is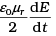 (symbols having usual meaning).
(symbols having usual meaning).
Ans. Let us assume Id be the displacement current in the region between two plates of parallel plate capacitor, in the figure.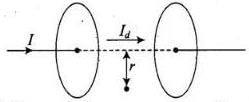 The magnetic field at a point between two plates of capacitor at a perpendicular distance r from the axis of plates is given by
The magnetic field at a point between two plates of capacitor at a perpendicular distance r from the axis of plates is given by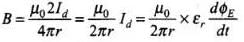
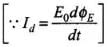
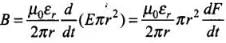
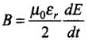
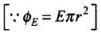
Q.22. Electromagnetic waves with wavelength
(i) λ1 is used in satellite communication.
(ii) λ2 is used to kill germs in water purifies.
(iii) λ3 is used to detect leakage of oil in underground pipelines.
(iv) λ4 is used to improve visibility in runways during fog and mist conditions.
(a) Identify and name the part of electromagnetic spectrum to which these radiations belong.
(b) Arrange these wavelengths in ascending order of their magnitude.
(c) Write one more application of each.
Ans. (a)
Solution.
(a) (i) In satellite communications, microwave is widely used. Hence λ1, is the wavelength of microwave.
(ii) In water purifier, ultraviolet rays are used to kill germs. So, λ2 is the wavelength of UV rays.
(iii) X-rays are used to detect leakage of oil in underground pipelines. So, λ3 is the wavelength of X-rays.
(iv) Infrared rays are used to improve visibility on runways during fog and mist conditions. So, it is the wavelength of infrared waves.
(b) Wavelength of X-rays < wavelength of UV < wavelength of infrared < wavelength of microwave.
=> λ3<λ2<λ4<λ1
(c)
| Radiation | Uses |
| γ - rays | Gives informations on nuclear structure , medical treatment etc. |
| X - rays | Medical diagnosis and treatment study of crystal structure , industrial radiograph . |
| UV - rays | Preserve food , sterilizing the surgical instruments, detecting the invisible writings, fingerprints etc. |
| Visible light | To see objects |
| Infrared rays | To treat, muscular strain for taking photography during the fog , haze etc. |
| Microwave and radio wave | In radar and telecommunication . |
Q.23. Show that average value of radiant flux density ‘S’ over a single period ‘T’ is given by S =  .
.
Solution.
Radiant flux density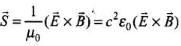
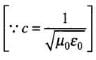
Let electromagnetic waves be propagating along x-axis. If electric field vector of electromagnetic wave be along y-axis, then magnetic field vector be along z-axis. Therefore,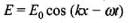
and B = B0 cos (kx - ωt)
E x B = (E0 x B0) cos2 (kx - ωt)
S = c2ε0(E x B)
= c2ε0(E0 x B0) cos2(kx - ωt)
Average value of the magnitude of radiant flux density over complete cycle is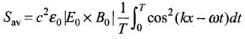
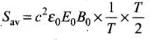
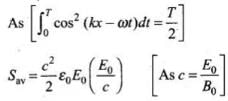
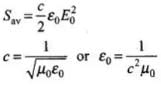
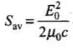 Hence Proved
Hence Proved
Q.24. You are given a 2µF parallel plate capacitor. How would you establish an instantaneous displacement current of 1mA in the space between its plates?
Ans. The capacitance of capacitor C = 2μF,
Displacement current Id = 1 mA
Charge in capacitor, q = CV
Iddt = CdV [∵ q = it]
or 
1 x 10-3 = 2 x 10-6 x dv/dt
or dv/dt = 1/2 x 103 = 500V/s
Hence by applying a varying potential difference of 500 V/s, we would produce a displacement current of desired value.
Q.25. Show that the radiation pressure exerted by an EM wave of intensity I on a surface kept in vacuum is I/C.
Ans. Let us consider a surface exposed to electromagnetic radiation. The radiation is falling normally on the surface. Further, intensity of radiation is I and area of surface exposed to radiation is A.
Ans. E - Energy received by surface per second = I. A
N = Number of photons received by surface per second.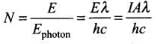
Let the surface is perfectly absorbing, 
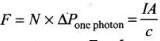
Also, Pressure P = F/A = 1/c
Q.26. What happens to the intensity of light from a bulb if the distance from the bulb is doubled? As a laser beam travels across the length of a room, its intensity essentially remains constant. What geometrical characteristic of LASER beam is responsible for the constant intensity which is missing in the case of light from the bulb?
Ans. We know intensity of light from a point source I α 1/r2, r is the distance from point source.
As the distance is doubled, so the intensity becomes one-fourth the initial value. But in case of laser it does not spread, so its intensity remain same.
Some geometrical characteristics of LASER beam which are responsible for the constant intensity is
(i) Unidirectional
(ii) Monochromatic
(iii) Coherent light
(iv) Highly collimated
These characteristics are missing in the case of normal light from the bulb.
Q.27. Even though an electric field E exerts a force qE on a charged particle yet the electric field of an EM wave does not contribute to the radiation pressure (but transfers energy). Explain.
Ans. The electric field of an electromagnetic wave is an oscillation field. It exerts electric force on a charged particle, but this electric force averaged over an integral number of cycles is zero, since its direction changes every half cycle. Hence, electric field is not responsible for radiation pressure though it transfer the energy. In fact, radiation pressure appears as a result of the action of the magnetic field of the wave on the electric currents induced by the electric field of the same wave.
LONG ANSWER TYPE QUESTIONS
Q.28. An infinitely long thin wire carrying a uniform linear static charge density λ is placed along the z-axis (Fig). The wire is set into motion along its length with a uniform velocity 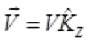 . Calculate the poynting vector
. Calculate the poynting vector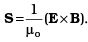
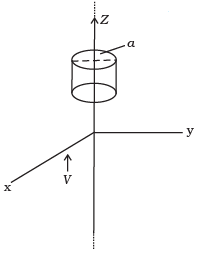
Ans. The electric field due to infinitely long thin wire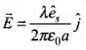
Magnetic field due to the wire,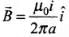
Equivalent current flowing through the wire, i = λv
Hence 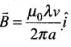
∴ 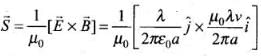
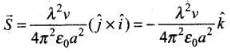
Q.29. Sea water at frequency ν = 4 × 108 Hz has permittivity ε ≈ 80 εo, permeability µ ≈ µo and resistivity ρ = 0.25 Ω–m. Imagine a parallel plate capacitor immersed in sea water and driven by an alternating voltage source V(t) = Vo sin (2π νt). What fraction of the conduction current density is the displacement current density?
Ans. Let the separation between the plates of capacitor immersed in sea water plates is d and applied voltage across the plates is V(t) = V0 sin (2πvt).
Thus, electric field, E = V(t)/d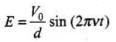
Now using Ohm's Law, the conduction current density 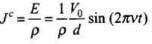
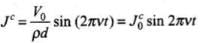
Here, 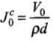
The displacement current density is given as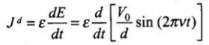
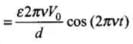
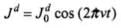
where, 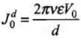
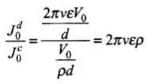
= 2π x 80εov x 0.25 = 4πε0v x 10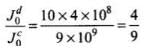
Q.30. A long straight cable of length l is placed symmetrically along z-axis and has radius a(<<l). The cable consists of a thin wire and a coaxial conducting tube. An alternating current I(t) = Io sin (2πνt) flows down the central thin wire and returns along the coaxial conducting tube. The induced electric field at a distance s from the wire inside the cable is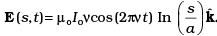
(i) Calculate the displacement current density inside the cable.
(ii) Integrate the displacement current density across the cross section of the cable to find the total displacement current Id.
(iii) Compare the conduction current I0 with the displacement current Iod .
Ans. We are given, the induced electric field at a distance r from the wire inside the cable.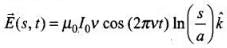
The displacement current density is given by
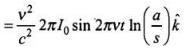
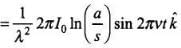
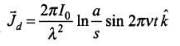
(ii) Total displacement current, Id =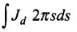
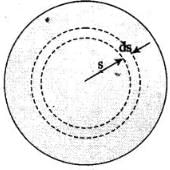
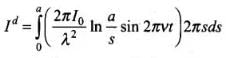
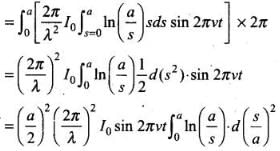
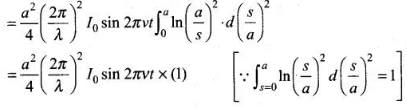
∴ 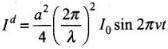
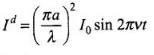
(iii) The displacement current,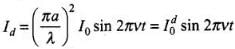
Here,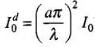
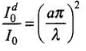
Q.31. A plane EM wave travelling in vacuum along z direction is given by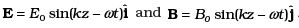
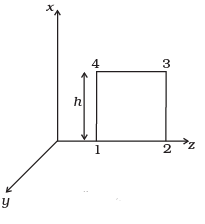
(i) Evaluate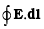 over the rectangular loop 1234 shown in Fig.
over the rectangular loop 1234 shown in Fig.
(ii) Evaluate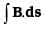 over the surface bounded by loop 1234.
over the surface bounded by loop 1234.
(iii) Use equation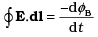 to prove Eo/B0 = c.
to prove Eo/B0 = c.
(iv) By using similar process and the equation 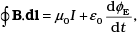
prove that c =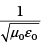
Ans. (i) Let electromagnetic wave is propagating along z-axis, in this case electric field vector (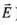 ) be along x-axis and magnetic field vector (
) be along x-axis and magnetic field vector (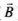 ) along y-axis, i.e.,
) along y-axis, i.e.,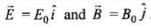 .
.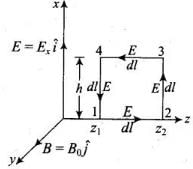
The line integral of E over the closed rectangular path 1234 in x-z plane of the figure is
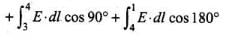
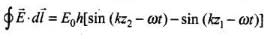 .......... (i)
.......... (i)
(ii) Now let us evaluate let us consider the rectangle 1234 to be made of strips of are ds = hdz each.
let us consider the rectangle 1234 to be made of strips of are ds = hdz each.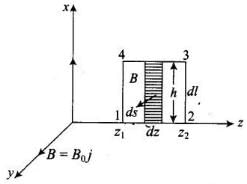
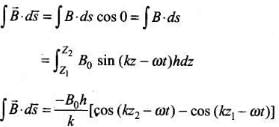 ................(ii)
................(ii)
(iii) We are given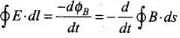
Substituting the values from Eqs. (i) and (ii), we get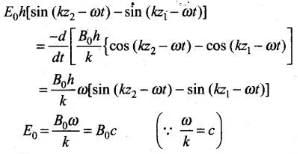
Eo/B0 = C
(iv) For evaluating 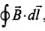 let us consider a loop 1234 in y-z plane as shown in figure given below.
let us consider a loop 1234 in y-z plane as shown in figure given below.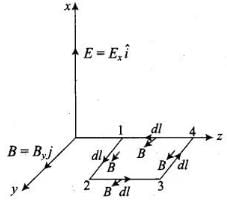
 .............. (iii)
.............. (iii)
Now to evaluate 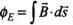 let us consider the rectangle 1234 to be made of strips of area hds each.
let us consider the rectangle 1234 to be made of strips of area hds each.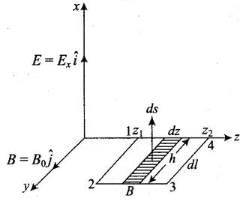
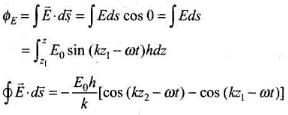
∴ 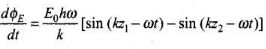 ........... (iv)
........... (iv)
Let  where I = conduction current
where I = conduction current
= 0 in vacuum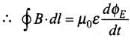
Using relations obtained in Eqs. (iii) and (iv) and simplifying, we get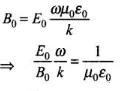
But E0/Bo = c and
therefore c =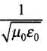
Q.32. A plane EM wave travelling along z direction is described by E = E0 sin(kz – ωt )ˆi and B = B0 sin(kz – ωt )ˆj . Show that
(i) The average energy density of the wave is given by 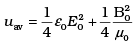
(ii) The time averaged intensity of the wave is given by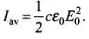
Ans. (i) Total energy carried by electromagnetic wave is due to electric field vector and magnetic field vector. In electromagnetic wave, E and B vary from point to point and from moment to moment.
The energy density due to electric field E is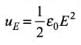
The energy density due to magnetic field B is 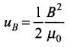
Total energy density of electromagnetic wave 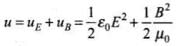
Let the HM wave be propagating along z-direction. The electric field vector and magnetic field vector be represented by
E = E0 sin (kz - ωt)
B = Bo sin (kz - ωt)
The values of E2 and B2 vary from point to point and from moment to moment. Hence, the effective values of E2 and B2 are their time averages over complete cycle.
We know,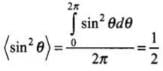
and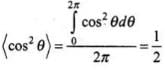
Hence, the time average value of E2 over complete cycle,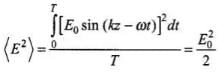
And, the time average value of B2 over complete cycle,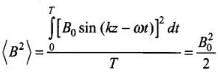
The time average of energy density over complete cycle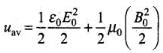
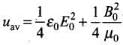
(ii) We know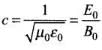
where μ0 = Absolute permeability, εo = Absolute permittivity, E0 and B0 = Amplitudes of electric field and magnetic field vectors.
The time average of energy density due to magnetic field B is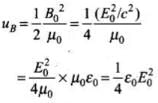
Hence, uB = uE; the time average of energy density due to magnetic field is equal to the time average of energy density due to electric field.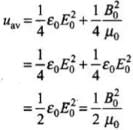
Time average intensity of the wave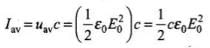
|
268 videos|780 docs|209 tests
|
FAQs on NCERT Exemplar: Electromagnetic Waves - Physics for JEE Main & Advanced
| 1. What are electromagnetic waves? |  |
| 2. How do electromagnetic waves propagate? |  |
| 3. What is the relationship between frequency and wavelength of electromagnetic waves? |  |
| 4. How do electromagnetic waves interact with matter? |  |
| 5. What are the applications of electromagnetic waves in our daily lives? |  |
















