Scientific Notation, Precision & Accuracy | Additional Study Material for NEET PDF Download
UNCERTAINTY IN MEASUREMENT
Many a times in the study of chemistry, one has to deal with experimental data as well as theoretical calculations. There are meaningful ways to handle the numbers conveniently and present the data realistically with certainty to the extent possible.
1. Scientific Notation
2. Significant Figures
3. Dimension Analysis
1. Scientific Notation
Scientific Notation is a way of expressing numbers that are too big or too small to be conveniently written in decimal form.
In which any number can be represented in the form N × 10n
(Where n is an exponent having positive or negative values and N can vary between 1 to 10).
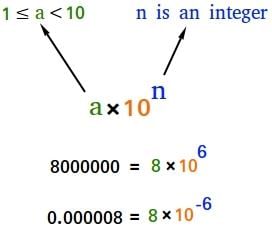 Scientific notation
Scientific notation
Example
- We can write 232.508 as 2.32508 × 102 in scientific notation. Similarly, 0.00016 can be written as 1.6 × 10–4.
- Thus, we can write 232.508 as 2.32508 × 102 in scientific notation. Note that while writing it, the decimal had to be moved to the left by two places and same is the exponent (2) of 10 in the scientific notation.
- Similarly, 0.00016 can be written as 1.6 × 10–4. Here the decimal has to be moved four places to the right and (– 4) is the exponent in the scientific notation.
MULTIPLICATION AND DIVISION FOR EXPONENTIAL NUMBERS
These two operations follow the same rules which are there for exponential numbers, i.e.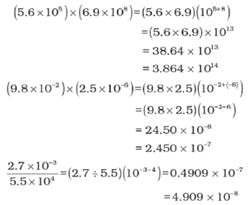
ADDITION AND SUBTRACTION FOR EXPONENTIAL NUMBERS
For these two operations, first the numbers are written in such a way that they have the same exponent. After that, the coefficients (digit terms) are added or subtracted as the case may be.
Thus, for adding 6.65 × 104 and 8.95 × 103, exponent is made same for both the numbers.
Thus, we get (6.65 × 104) + (0.895 × 104)
PRECISION AND ACCURACY
Every experimental measurement has some amount of uncertainty associated with it. However, one would always like the results to be precise and accurate. Precision and accuracy are often referred to while we talk about the measurement.
Precision and accuracy are often referred to while we talk about the measurement.
Accuracy refers to the closeness of a measured value to a standard or known value
Example: if in lab you obtain a weight measurement of 3.2 kg for a given substance, but the actual or known weight is 10 kg, then your measurement is not accurate. In this case, your measurement is not close to the known value.
Precision refers to the closeness of two or more measurements to each other.
Using the example above, if you weigh a given substance five times, and get 3.2 kg each time, then your measurement is very precise. Precision is independent of accuracy. You can be very precise but inaccurate, as described above. You can also be accurate but imprecise.
Example: If on average, your measurements for a given substance are close to the known value, but the measurements are far from each other, then you have accuracy without precision.
Example
If the true value for a result is 2.00 g.
(a) Student ‘A’ takes two measurements and reports the results as 1.95 g and 1.93 g.
- These values are precise as they are close to each other but are not accurate.
(b) Another student repeats the experiment and obtains 1.94 g and 2.05 g as the results for two measurements.
- These observations are neither precise nor accurate.
(c) When a third student repeats these measurements and reports 2.01g and 1.99 g as the result.
- These values are both precise and accurate.

Examples:
Q.1. Which of the following options is not correct?
(a) 8008 = 8.008 x 103
(b) 208 = 3
(c) 5000 = 5.0 x 103
(d) 2.0034 = 4
Ans: (d)
Solution:
2.0034 = 4
Q.2. Exponential notation in which any number can be represented in the form, Nx 10n here N is termed as
(a) non –digit term
(b) digit term
(c) numeral
(d) base term
Ans: (b)
Solution:
In exponential notation N × 10n, N is a number called digit term which varies between 1.000 and 9.000….
Q.3. In scientific notation,0.00016 can be written as
(a) 1.6 x 10-4
(b) 1.6 x 10-3
(c) 1.6 x 10-2
(d) 1.6 x 10-1
Ans: (a)
Solution:
0.00016 can be written as 1.6 × 10-4 in scientific notation
4. Addition of 6.65 x 104 and 8.95 x 103, in terms of scientific notation will be
(a) 7.545 104
(b) 75.45 10 3
(c) 754.5 102
(d) 75.45 100
Ans: (a)
Solution:
6.65 × 104 + 8.95 × 103
= (6.65 + 0.895) × 104 = 7.545 × 104
Q.5. The substraction of two numbers
2.5 x 10-2 -4.8 x 10 -3 gives the following value.
(a) 2.02 x 10-3
(b) 2.02 x 10-2
(c) 2.02 x 10-1
(d) 2.02 x 100
Ans: (b)
Solution:
2.5 × 10-2 - 4.8 × 10-3
= 2.5 × 10-2 — (0.48 × 10-2) = 2.02 × 10-2
Q.6. A refers to the closeness of various measurements for the same quantity. B is the agreement of a particular value to the true value of the result. A and B respective are
(a) A → Significant figures, B → accuracy
(b) A → accuracy, B → precision
(c) A → Precision, B → accuracy
(d) A → significant figures, → precision
Ans: (c)
Q.7. Which of the following statement is/are true?
(a) Every experimental measurement has zero amount of uncertainty associated with it
(b) One would always like the result to be precise and accurate
(c) Precision and accuracy are often referred to while we talk about the measurement
(d) Both (b) and (c)
Ans: (d)
Solution:
Every experimental measurement has some amount of uncertainty associated with it.
Try Yourself!
|
26 videos|312 docs|64 tests
|
FAQs on Scientific Notation, Precision & Accuracy - Additional Study Material for NEET
| 1. What is scientific notation and why is it important in scientific calculations? |  |
| 2. How can precision and accuracy be differentiated in scientific measurements? |  |
| 3. What are some common sources of error in scientific measurements and how can they be minimized? |  |
| 4. How is scientific notation used in representing physical constants and measurements? |  |
| 5. How can scientific notation be converted to decimal form and vice versa? |  |
















