Concept of Successive division & Remainder problems on different models of HCF and LCM - Quant PDF Download
SUCCESSIVE DIVISION
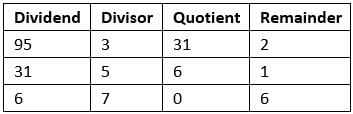
If we divide a number by a particular number then again divide the resulting quotient by a number, and again… this is called Successive division. Let us try to understand the concept through an example.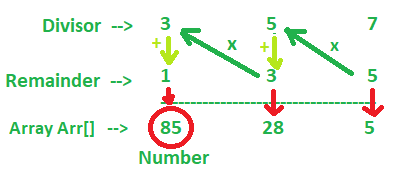
The next step is to divide the quotient obtained in this division with 5, i.e. 58/5, which will give a quotient of 11 and a remainder of 3. And now again we have to divide the quotient obtained in the last division with 3, 11/3, which will give a quotient of 3 and a remainder of 2.
So, when 352 is divided by 6, 5, and 3 successively we obtained a remainder of 4, 3, and 2 respectively. This is called successive division.
So, from the concept we saw above a question can be framed that, If a number when successively divided by 6, 5, and 3 leaves the remainders 4, 3, and 2 respectively. Find the number.
The number can be calculated as follows:
According to the concept explained below:
Step 1: Write the divisors of the division along a horizontal line.
Step 2: Write the respective remainders under the divisors.
Divisors → 6 5 3
Remainder → 4 3 2
Now, the last remainder has to be multiplied by the second divisor and then added to the second remainder, the result obtained is again multiplies by the first divisor and then added to the first remainder.
The result of the above calculation will be:
{(2 * 5) + 3} * 6 + 4 = 82
82 will be the smallest number, when successively divided by 6, 5, and 3 to leave the remainders 4, 3, and 2 respectively.
⇒ Now, the other numbers which give the same remainders when successively divided by 6,5, and 3 will be of the form.
(6 * 5 * 3) k + 82, or 90k + 82.
Step 1: Write the divisors of the division along a horizontal line.
Step 2: Write the respective remainders under the divisors.
So. the arrangement of numbers is as below, when 247 is successively divided by 7,3 and 2.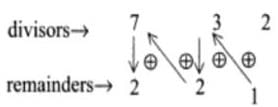
Step 3: Starting from the last remainder, multiply the number along the inclined line, then add the number along the vertical line.
Repeat the process until the first remainder is reached.
The result of the above calculation is :
[(1 × 3) + 2 ] × 7 + 2 = 5 × 7 + 2 = 37
37 is the lowest number that leaves the remainders 2, 2 and 1 when successively divided by 7 , 3 and 2.
Other numbers that have the same remainders are given by the form (7 × 3 × 2)k + 37 or 42k + 37.
Note: Where 4 = 5, value of 42k + 37 = 247, which is the number shown in the example.
The above is generalized and written as:
N = (d1, d2, d3 . . . . . . . )k + (least value).
where d1 d2, d3} etc., are the divisors of the successive division and least value is the value which is calculated as shown above.
Sample problem
1. If a number when successively divided by 7, 5, and 3 leaves the remainders 4, 2, and 1 respectively. Find the smallest such number.
(a) 42
(b) 53
(c) 67
(d) 73
Solution.
This is a problem of successive division.
Divisors 7 5 3
Remainders 4 2 1
REMAINDER PROBLEMS on different models of HCF and LCM
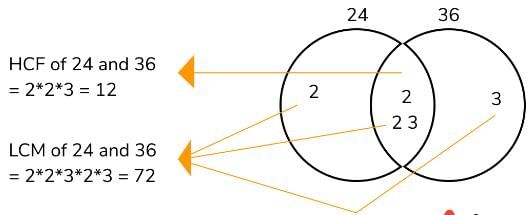
- The greatest number that will exactly divide by x, y, and z will be the Highest common factor of x, y, and z which is HCF (x, y, z).
- The least number that will be exactly divisible by x, y, and z will be the Least common multiple of x, y, and z which is LCM (x, y, z).
- A number N when divided by positive integers a, b and c leaves different remainders p, q and r such that the difference between the divisors and their respective remainders are equal then the smallest value of N = LCM (a, b, c) – d.
- A number N when divided by positive integers a, b and c leaves same remainder r in each case, then the number will be N = K * LCM (p, q, and r) + r
- The greatest number when divided by x, y and z leaving different remainders a, b, and c respectively = HCF (x - a, y - b, z - c).
- The greatest number when divided by x, y and z leaving the same remainder will be HCF ((x - y), (y - z), (z - x))
LCM Models

HCF Models
Sample Problems
Q.1. What is the greatest number that will exactly divide 841, 348, and 638 leaving no remainder?
(a) 9
(b) 29
(c) 58
(d) 87
Ans. (b)
Solution.
The greatest number that will be exactly divide by 841, 348, and 638 will be the Highest common factor of 841, 348, and 638 i.e. HCF (841, 348, and 638)
The HCF of the three numbers will be 29.
∴ 29 is the greatest number that will exactly divide 841, 348, and 638 leaving no remainder.
FAQs on Concept of Successive division & Remainder problems on different models of HCF and LCM - Quant
| 1. What is the concept of successive division and remainder problems in HCF and LCM? |  |
| 2. How can we solve HCF and LCM problems using the concept of successive division and remainder? |  |
| 3. Can you explain the different models of HCF and LCM in successive division and remainder problems? |  |
| 4. What are some tips to solve successive division and remainder problems on different models of HCF and LCM? |  |
| 5. How does understanding successive division and remainder problems in HCF and LCM help in competitive exams? |  |