NCERT Exemplar - Determinants(Part-2) | Mathematics (Maths) Class 12 - JEE PDF Download
Objective Type Questions (M.C.Q.)
Q.24. If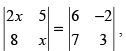 then value of x is
then value of x is
(a) 3
(b) ± 3
(c) ± 6
(d) 6
Ans. (c)
Solution.
Given that
⇒ 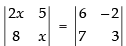
⇒ 2x2 – 40 = 18 + 14 ⇒ 2x2 = 32 + 40
⇒ 2x2 = 72 ⇒ x2 = 36
∴ x = ± 6
Hence, the correct option is (c).
Q.25. The value of determinant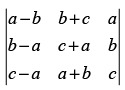
(a) a3 + b3 + c3
(b) 3bc
(c) a3 + b3 + c3 – 3abc
(d) None of these
Ans. (d)
Solution.
Here, we have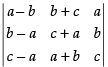
C2 → C2 + C3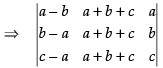
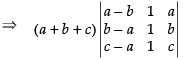
(Taking a + b + c common from C2)
R1 → R1 - R2, R2 → R2 - R3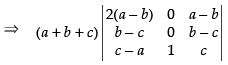
Expanding along C2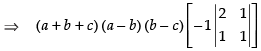
⇒ (a + b + c) (a - b) (b - c) (- 1)
⇒ (a + b + c) (a - b) (c - b)
Hence, the correct option is (d).
Q.26. The area of a triangle with vertices (–3, 0), (3, 0) and (0, k) is 9 sq. units. The value of k will be
(a) 9
(b) 3
(c) – 9
(d) 6
Ans. (b)
Solution.
Area of triangle with vertices (x1 y1), (x2 y2) and (x3, y3) will be: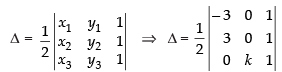
⇒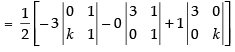
⇒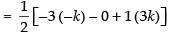
⇒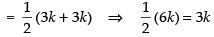
3k = 9 ⇒ k = 3
Hence, the correct option is (b).
Q.27. The determinant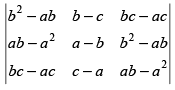 equals
equals
(a) abc (b – c) (c – a) (a – b)
(b) (b – c) (c – a) (a – b)
(c) (a + b + c) (b – c) (c – a) (a – b)
(d) None of these
Ans. (d)
Solution.
Let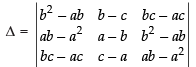
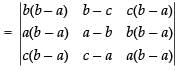
(Taking (b – a) common from C1 and C3)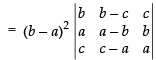
C1 → C1 - C3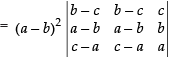
(C1 and C2 are identical columns.)
= (a – b)2 × 0
= 0
Hence, the correct option is (d).
Q.28. The number of distinct real roots of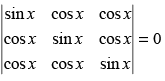 in the interval
in the interval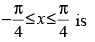
(a) 0
(b) 2
(c) 1
(d) 3
Ans. (c)
Solution.
Given that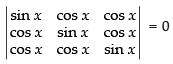
C1 → C1 + C2 + C3
⇒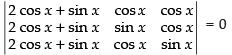
Taking 2 cos x + sin x common from C1
⇒
R1 → R1 - R2, R2 → R2 - R3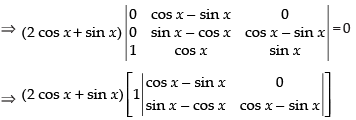
⇒ (2 cos x + sin x) (cos x – sin x)2 = 0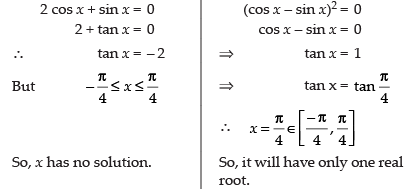
Hence, the correct option is (c).
Q.29. If A, B and C are angles of a triangle, then the determinant is equal to
is equal to
(a) 0
(b) – 1
(c) 1
(d) None of these
Ans. (a)
Solution.
Let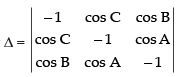
C1 → aC1 + bC2 + cC3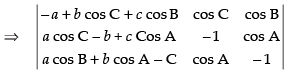
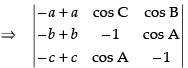
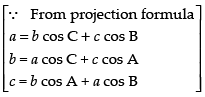
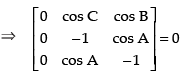
Hence, the correct option is (a).
Q.30. Let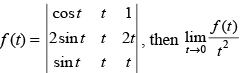 is equal to
is equal to
(a) 0
(b) – 1
(c) 2
(d) 3
Ans. (a)
Solution.
We have f(t) =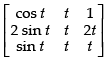
Expanding along R1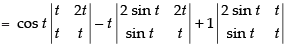
= cos t(t2 - 2t2 ) - t( 2t sint - 2t sint )+ ( 2t sint- t sint )
= -t2 cos t+ t sin t
∴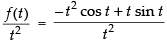
⇒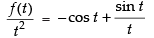
⇒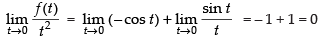
Hence, the correct option is (a).
Q.31. The maximum value of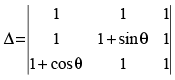 is (θ is real number)
is (θ is real number)
(a) 1/2
(b) √3/2
(c) √2
(d) 2√3/4
Ans. (a)
Solution.
Given that: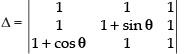
C1 → C1 - C2, C2 → C2 - C3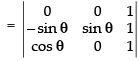
Expanding along R1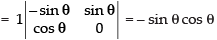
⇒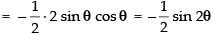
but maximum value of sin 2θ = 1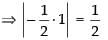
Hence, the correct option is (a).
Q.32. If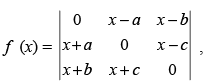 then
then
(a) f (a) = 0
(b) f (b) = 0
(c) f (0) = 0
(d) f (1) = 0
Ans. (c)
Solution.
Given that: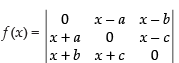
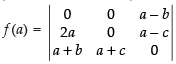
Expanding along R1 =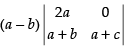
= (a – b) [2a(a + c)] = (a – b) × 2a × (a + c) ≠ 0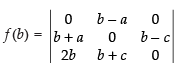
Expanding along R1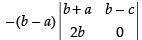
= - (b - a) [( - 2b) (b - c)] = 2b(b – a) (b – c) ≠ 0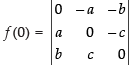
Expanding along R1 =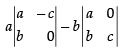
= a(bc) – b(ac)= abc – abc = 0
Hence, the correct option is (c).
Q.33. If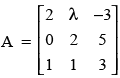 , then A–1 exists if
, then A–1 exists if
(a) λ = 2
(b) λ ≠ 2
(c) λ ≠ – 2
(d) None of these
Ans. (d)
Solution.
We have,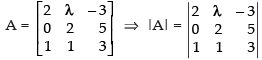
Expanding along R1 =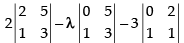
= 2(6 – 5) – λ(0 – 5) – 3(0 – 2)
= 2 + 5λ + 6 = 8 + 5λ
If A–1 exists then |A| ≠ 0
∴ 8 + 5λ ≠ 0 so λ ≠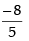
Hence, the correct option is (d).
Q.34. If A and B are invertible matrices, then which of the following is not correct?
(a) adj A = |A| × A-1
(b) det (A)-1 = [det(A)]-1
(c) (AB)-1 = B-1A-1
(d) (A + B)-1 = B-1 + A-1
Ans. (d)
Solution.
If A and B are two invertible matrices then
(a) adj A = |A| × A-1 is correct
(b) det (A)–1 = [det(A)]–1 =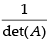 is correct
is correct
(c) Also, (AB)–1 = B–1A–1 is correct
(d) (A + B)-1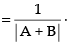 adj (A + B)
adj (A + B)
∴ (A + B)-1 ≠ B-1+ A-1
Hence, the correct option is (d).
Q.35. If x, y, z are all different from zero and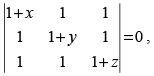 then value of x–1 + y–1 + z–1 is
then value of x–1 + y–1 + z–1 is
(a) xyz
(b) x–1y–1z–1
(c) – x – y – z
(d) –1
Ans. (d)
Solution.
Given that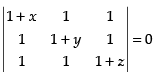
Taking x, y and z common from R1, R2 and R3 respectively.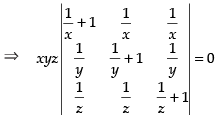
R1 → R1 + R2 + R3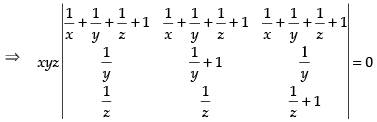
Taking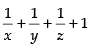 common from R1
common from R1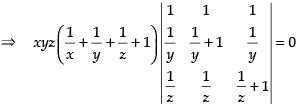
C1 → C1 - C2, C2 → C2 - C3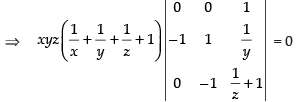
Expanding along R1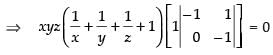
⇒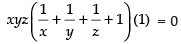
⇒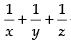 + 1 = 0 and xyz ≠ 0 (x ≠ y ≠ z ≠ 0)
+ 1 = 0 and xyz ≠ 0 (x ≠ y ≠ z ≠ 0)
∴ x–1 + y–1 + z–1 = – 1
Hence, the correct option is (d).
Q.36. The value of the determinant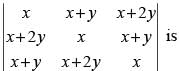
(a) 9x2(x + y)
(b) 9y2(x + y)
(c) 3y2(x + y)
(d) 7x2(x + y)
Ans. (b)
Solution.
Let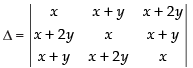
C1 → C1 + C2 + C3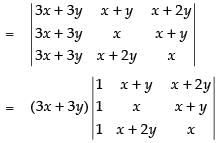
[Taking (3x + 3y) common from C1]
R1 → R1 - R2, R2 → R2 - R3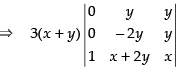
Expanding along C1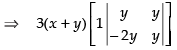
⇒ 3(x + y) (y2 + 2y2) ⇒ 3(x + y) (3y2) ⇒ 9y2(x + y)
Hence, the correct option is (b).
Q.37. There are two values of a which makes determinant,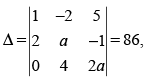 then sum of these number is
then sum of these number is
(a) 4
(b) 5
(c) – 4
(d) 9
Ans. (c)
Solution.
Given that,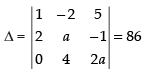
Expanding along C1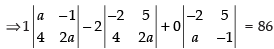
⇒ (2a2 + 4) – 2(– 4a – 20) = 86
⇒ 2a2 + 4 + 8a + 40 = 86
⇒ 2a2 + 8a + 4 + 40 – 86 = 0
⇒ 2a2 + 8a – 42 = 0
⇒ a2 + 4a – 21 = 0
⇒ a2 + 7a – 3a – 21 = 0
⇒ a(a + 7) – 3(a + 7) = 0
⇒ (a – 3) (a + 7) = 0
∴ a = 3, – 7
Required sum of the two numbers = 3 – 7 = – 4.
Hence, the correct option is (c).
Fill in the blanks
Q.38. If A is a matrix of order 3 × 3, then |3A| = _______ .
Ans.
We know that for a matrix of order 3 × 3,
|KA| = K3 |A|
∴ 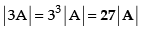
Q.39. If A is invertible matrix of order 3 × 3, then |A –1 | _______ .
Ans.
We know that for an invertible matrix A of any order,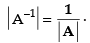
Q.40. If x, y, z ∈ R, then the value of determinant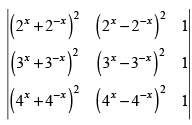 is equal to _______.
is equal to _______.
Ans.
We have,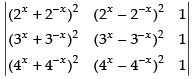
C1 → C1 - C2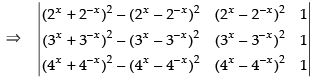
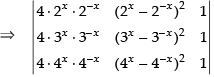 [applying (a + b)2 – (a – b)2 = 4ab]
[applying (a + b)2 – (a – b)2 = 4ab]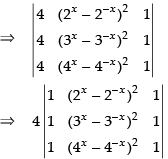
(Taking 4 common from C1)
⇒ 4 × 0 = 0 (∵ C1 and C3 are identical columns)
Q.41. If cos 2θ = 0,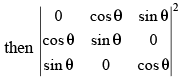 =_______ .
=_______ .
Ans.
Given that: cos 2θ = 0
⇒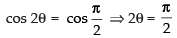
∴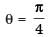
The determinant can be written as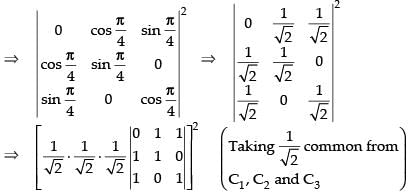
Expanding along C1,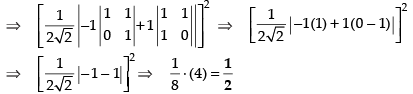
Q.42. If A is a matrix of order 3 × 3, then (A 2)–1 = ________.
Ans.
For any square matrix A, (A2)–1 = (A–1)2.
Q.43. If A is a matrix of order 3 × 3, then number of minors in determinant of A are ________.
Ans.
The order of a matrix is 3 × 3
∴ Total number of elements = 3 × 3 = 9
Hence, the number of minors in the determinant is 9.
Q.44. The sum of the products of elements of any row with the co-factors of corresponding elements is equal to _________.
Ans.
The sum of the products of elements of any row with the co-factors of corresponding elements is equal to the value of the determinant of the given matrix.
Let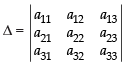
Expanding along R1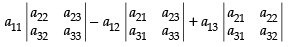
⇒ a11M11 + a12M12 + a13M13
(where M11, M12 and M13 are the minors of the corresponding elements)
Q.45. If x = – 9 is a root of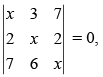 then other two roots are __________.
then other two roots are __________.
Ans.
We have,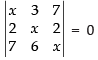
Expanding along R1
⇒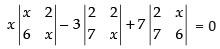
⇒ x(x2 – 12) – 3(2x – 14) + 7(12 – 7x) = 0
⇒ x3 – 12x –6x + 42 + 84 – 49x = 0
x3 – 67x + 126 = 0 ...(1)
The roots of the equation may be the factors of 126 i.e., 2 × 7 × 9
9 is given the root of the determinant put x = 2 in eq. (1)
(2)3 – 67 × 2 + 126 ⇒ 8 - 134 + 126 = 0
Hence, x = 2 is the other root.
Now, put x = 7 in eq. (1)
(7)3 – 67(7) + 126 ⇒ 343 - 469 + 126 = 0
Hence, x = 7 is also the other root of the determinant.
Q.46. 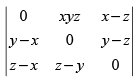 = _______.
= _______.
Ans.
Let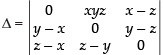
C1 → C1 – C3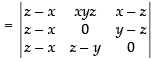
Taking (z – x) common from C1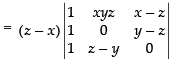
R1 → R1 - R2, R2 → R2 - R3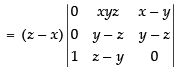
Taking (y – z) common from R2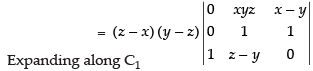
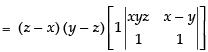
= (z – x) (y – z) (xyz – x + y) = (y – z) (z – x) (y – x + xyz)
Q.47. If f(x) =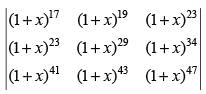 = A + Bx + Cx2 + ..., then A = ________.
= A + Bx + Cx2 + ..., then A = ________.
Ans.
Given that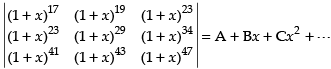
Taking (1 + x)17, (1 + x)23 and (1 + x)41 common from R1, R2 and R3 respectively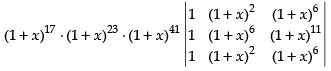
⇒ (1 + x)17 . (1+x)23 . (1+x)41 . 0 (R1 and R3 are identical)
∴ 0 = A + Bx + Cx2 + &
By comparing the like terms, we get A = 0.
State True or False for the statements of the following Exercises:
Q.48. ( A3 ) –1 = ( A −1 )3 , where A is a square matrix and |A| ≠ 0.
Ans.
Since (AK)–1 = (A–1)K where K ∈ N
So, (A3)-1 = (A-1)3 is true
Q.49. 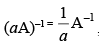 , where a is any real number and A is a square matrix.
, where a is any real number and A is a square matrix.
Ans.
If A is a non-singular square matrix, then for any non-zero
scalar ‘a‘, aA is invertible.
∴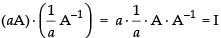
So, (aA) is inverse of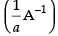
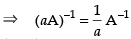 is true.
is true.
Q.50. |A–1| ≠ |A|–1 , where A is non-singular matrix.
Ans.
False.
Since 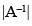 =
= 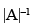 for a non-singular matrix.
for a non-singular matrix.
Q.51. If A and B are matrices of order 3 and |A| = 5 , |B| = 3 , then |3AB| = 27 × 5 × 3 = 405.
Ans.
True.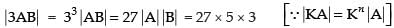
Q.52. If the value of a third order determinant is 12, then the value of the determinant formed by replacing each element by its co-factor will be 144.
Ans.
True.
Since 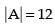
If A is a square matrix of order n
then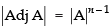
∴ 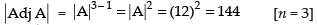
Q.53. 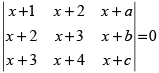 , where a, b, c are in A.P.
, where a, b, c are in A.P.
Ans.
True.
Let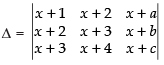
R2 → 2R2 - (R1 + R3)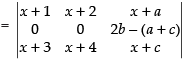
a, b, c are in A.P.
∴ b – a = c – b ⇒ 2b = a + c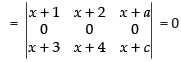
Q.54. |adj. A| = |A|2 , where A is a square matrix of order two.
Ans.
False.
Since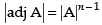 where n is the order of the square matrix.
where n is the order of the square matrix.
Q.55. The determinant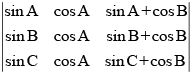 is equal to zero.
is equal to zero.
Ans.
True.
Let
Splitting up C3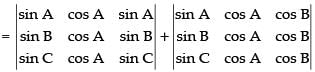
 [∵ C1 and C3 are identical]
[∵ C1 and C3 are identical]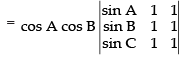
[Taking cos A and cos B common from C2 and C3 respectively]
= cos A cos B (0) [∵ C2 and C3 are identical]
= 0
Q.56. If the determinant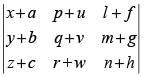 splits into exactly K determinants of order 3, each element of which contains only one term, then the value of K is 8.
splits into exactly K determinants of order 3, each element of which contains only one term, then the value of K is 8.
Ans.
True.
Let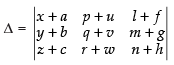
Splitting up C1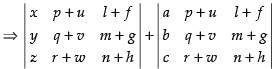
Splitting up C2 in both determinants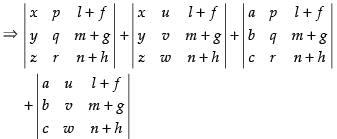
Similarly by splitting C3 in each determinant, we will get 8 determinants.
Q.57. Let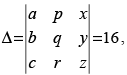 then
then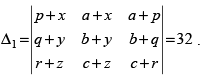
Ans. True.
Given that:
L.H.S.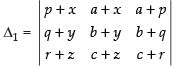
C1 → C1 + C2 + C3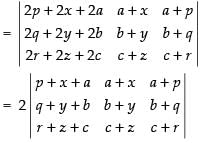
[Taking 2 common from C1]
C1 → C1 - C2 =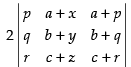
C3 → C3 - C1d =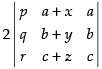
Splitting up C2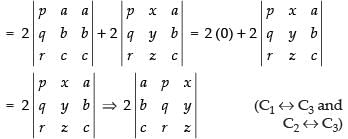
= 2 × 16 = 32
Q.58. The maximum value of
Ans.
True.
Let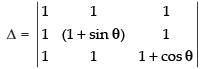
C1 → C1 - C2, C2 → C2 - C3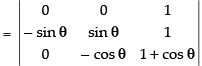
Expanding along C3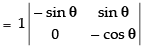 = sin θ cos θ – 0 = sin θ cos θ
= sin θ cos θ – 0 = sin θ cos θ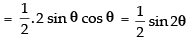
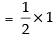 [Maximum value of sin 2θ = 1]
[Maximum value of sin 2θ = 1]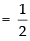
|
223 videos|377 docs|167 tests
|
FAQs on NCERT Exemplar - Determinants(Part-2) - Mathematics (Maths) Class 12 - JEE
| 1. What are the properties of determinants? |  |
| 2. How can we find the determinant of a 2x2 matrix? |  |
| 3. Can a determinant have a negative value? |  |
| 4. What is the significance of determinants in linear algebra? |  |
| 5. Is it possible to have a zero determinant for a non-zero matrix? |  |





















