Class 9 Maths - Number System CBSE Worksheets- 1
Q.1. Which of the following is an irrational number?
(a) 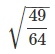
(b) √3
(c) 1/2
(d) 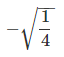
Ans.
An irrational number is a number that cannot be expressed as a fraction of two integers and has an infinite non-repeating decimal representation. Let's evaluate the options:
(a) √49/64: This is a rational number because both the numerator and denominator are perfect squares, and their square root can be expressed as a fraction of integers. √49/64 = 7/8.
(b) √3: This is an irrational number because the square root of 3 cannot be expressed as a fraction of integers, and its decimal representation goes on infinitely without repeating.
(c) 1/2: This is a rational number because it can be expressed as a fraction of integers.
(d) -√1/4: This is a rational number because √1/4 = 1/2, and the negative sign only changes the sign of the rational number.
So, the irrational number among the given options is: (b) √3
Q.2. The number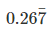 in p/q form is
in p/q form is
(a) 267/1000
(b) 26/10
(c) 241/900
(d) 241/999
Ans. (c)
Solution:
let x be the p/q form, x =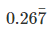
multiply both side by 100,
100 x = 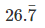 ...(i)
...(i)
multiply both side by 10
1000 x = 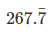 ....(ii)
....(ii)
Subtract (ii) - (i)
1000 x - 100 x = 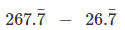
900 x = 241
⇒ x = 241/900
Hence, option (c) is correct
Q.4. The decimal representation of a rational number is either:
(a) Terminating or repeating
(b) Non-terminating and non-repeating
(c) Only terminating
(d) Only repeating
Ans: (a) Terminating or repeating
- A rational number is any number that can be expressed as a fraction , where p and q are integers and
A terminating decimal is one that has a finite number of digits after the decimal point.
A repeating decimal is one where a block of digits repeats infinitely.
Q.5. Insert 3 irrational number between 2.6 and 3.8
Ans. 2.6 and 3.8
Irrational numbers are non repeating non - terminating
2.61010010001.....
2.802002000200002......
3.604004000400004.......
Q.6. What is the decimal form of the following no's.
(a) 18/11
(b) 3/26
(c) 1/17
(d) 2/13
Ans.
(a) 18/11 = 1.63636363...
(b) 3/26 = 0.11538461538
(c) 1/17 = 0.05882352941
(d) 2/13 = 0.15384615384
Q.8. Simplify: 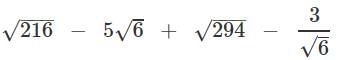
Ans.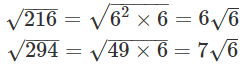
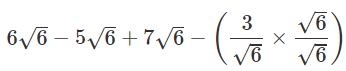
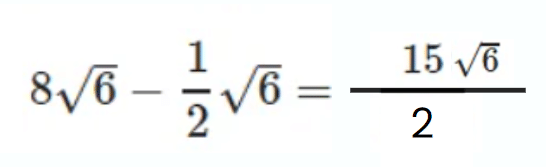
Q.9. Rationalise: 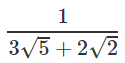
Ans.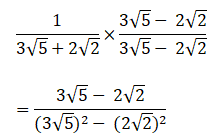
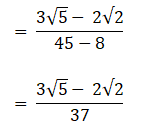
Q.10. Find the value of 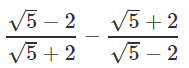
Ans.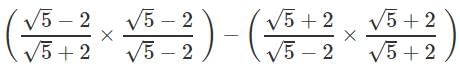
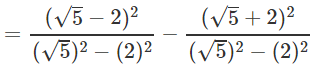
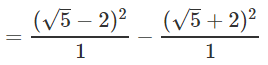
= 5+4 - 4√5 - 5 - 4 - 4√5 = -8√5
Q.11. If 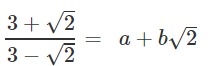 ,
,
find the value of a & b.
Ans.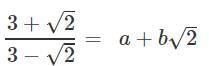
Rationalising LHS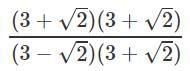
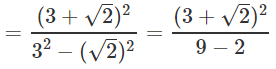
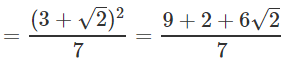
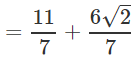
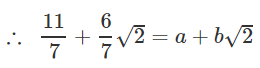
∴ a = 11/7 and b = 6/7
Q.12. Evaluate: 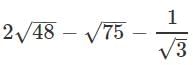
Ans.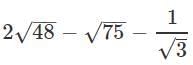
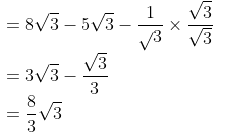
Q.13. Write the value of 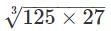
Ans.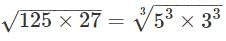
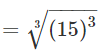
= 15
Q.14. Express 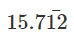 in p/q form.
in p/q form.
Ans.
let x be the p/q form,
so, x = 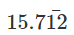
10x = 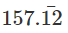
1000x = 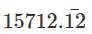
1000x - 10x = 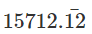 -
- 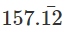
990x = 15555
x= 15555/990
= 1037/66
Q.15. Insert five rational no's between 3/5 and 4/5.
Ans.
3/5 and 4/5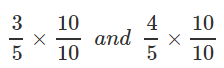
30/50 and 40/50
∴ pick any five number between 30 and 40
31/50, 32/50, 36/50, 37/50, 39/50
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths - Number System CBSE Worksheets- 1
| 1. What is the definition of a number system in mathematics? |  |
| 2. What are the different types of number systems taught in Grade 9? |  |
| 3. How do you convert a fraction into a decimal? |  |
| 4. What is the difference between rational and irrational numbers? |  |
| 5. How can I determine if a number is rational or irrational? |  |






















