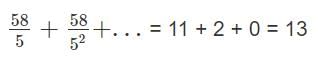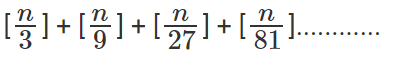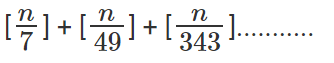Important Concepts: Number System - 2 | General Test Preparation for CUET UG - CUET Commerce PDF Download
| Table of contents |

|
| Unit Digit |

|
| Cyclicity Table |

|
| Number of Zeroes |

|
| Solved Examples |

|
This document covers unit digits and their repeating patterns when raised to powers (cyclicity), explaining how certain digits have fixed or cyclic unit digits. It also discusses how to determine the number of trailing zeros in expressions and factorials, focusing on the role of factors 2 and 5. Examples and solutions are provided to illustrate these concepts.
Unit Digit
- To understand the concept of the unit digit, we must know the concept of cyclicity. This concept is mainly about the unit digit of a number and its repetitive pattern of being divided by a certain number.

- The concept of the unit digit can be learned by figuring out the unit digits of all the single-digit numbers from 0 - 9 when raised to certain powers.
- These numbers can be broadly classified into three categories for this purpose:
1. Digits 0, 1, 5, & 6:
When we observe the behaviour of these digits, they all have the same unit's digit as the number itself when raised to any power, i.e. 0n = 0, 1n =1, 5n = 5, 6n = 6.
5 2 = 25: Unit digit is 5, the number itself.
16 = 1: Unit digit is 1, the number itself.
04 = 0: Unit digit is 0, the number itself.
63 = 216: Unit digit is 6, the number itself.
Let's apply this concept to the following example.
Example: Find the unit digit of the following numbers:
- 185563
Answer= 5 - 2716987
Answer= 1 - 15625369
Answer= 6 - 190654789321
Answer= 0
2. Digits 4 & 9:
Both these numbers have a cyclicity of only two different digits as their unit's digit.
42 = 16: Unit digit is 6.
43 = 64: Unit digit is 4.
44 = 256: Unit digit is 6.
45 = 1024: Unit digit is 4.
92 = 81: Unit digit is 1.
93 = 729: Unit digit is 9.
It can be observed that the unit digits 6 and 4 are repeating in an odd-even order. So, 4 has a cyclicity of 2. Similar is the case with 9.
It can be generalized as follows:
 Example: Find the unit digit of following numbers:
Example: Find the unit digit of following numbers:
- 189562589743
Answer = 9 (since power is odd) - 279698745832
Answer = 1(since power is even) - 154258741369
Answer = 4 (since power is odd) - 19465478932
Answer = 6 (since power is even)
3. Digits 2, 3, 7, & 8:
These numbers have a power cycle of 4 different numbers.
21 = 2, 22 = 4, 23 = 8 & 24 = 16 and after that it starts repeating.
So, the cyclicity of 2 has 4 different numbers 2, 4, 8, 6.
31 = 3, 32 = 9, 33 = 27 & 34 = 81 and after that it starts repeating.
So, the cyclicity of 3 has 4 different numbers 3, 9, 7, 1.
7 and 8 follow similar logic.
So these four digits, i.e. 2, 3, 7 and 8 have a unit digit cyclicity of four steps.
Cyclicity Table
The concepts discussed above are summarized in the given table.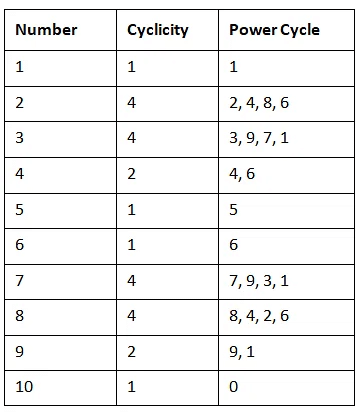
The power concept or cyclicity of a number helps us figure out the last digit of a number raised to a large power without actually calculating the whole thing. It's based on a repeating pattern that depends on the last digit of the number. A table helps us predict this last digit. Also, digits that appear once or twice repeat every four times. So, each digit repeats every four times.
Number of Zeroes
1. Number Of Zeros in An Expression
Step 1
- Suppose you have to find the number of zeroes in a product: 24 × 32 × 17 × 23 × 19.
- We first get the series in terms of its prime factors i.e. 23∗31∗25∗171∗19∗23.
- As you can notice, this product will have no zeroes because it has no 5 in it.
- However, if you have an expression like: 8 × 15 × 23 × 17 × 25 × 22
- The above expression can be rewritten in the standard form as: 23∗31∗51∗23∗17∗52∗21∗111
Step 2
- Zeroes are formed by a combination of 2 × 5.
- Hence, the number of zeroes will depend on the number of pairs of 2’s and 5’s that can be formed.
- In the above product, there are four twos and three fives. Hence, we shall be able to form only three pairs of (2 × 5).
- Hence, there will be 3 zeroes in the product.
2. Finding the Number of Zeros in a Factorial Value
- Method 1: Suppose you had to find the number of zeroes in 6!. 6! = 6 × 5 × 4 × 3 × 2 × 1 = (3 × 2) × (5) × (2 × 2) × (3) × (2) × (1).
Counting the number of 5 will give the answer. - Method 2 : For finding the zeroes in 6! we use
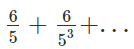 So we get 1 as the answer as all divisions after the first term in the series are in decimals, which we ignore.
So we get 1 as the answer as all divisions after the first term in the series are in decimals, which we ignore.
Example: Finding the Number of Zeros in 12 × 15 × 5 × 24 × 13 × 17
(a) 0
(b) 1
(c) 2
(d) 3
Ans: (c)
Sol: To find the number of zeros in the product, we look for pairs of factors 2 and 5, as each pair forms a trailing zero.Prime factorization:
12 = 2² × 3 ,15 = 3 × 5, 5 = 5, 24 = 2³ × 3, 13 = 13, 17 = 17
Now, count the factors of 2 and 5:
Factors of 2: 2 (from 12) + 3 (from 24) = 5 factors of 2
Factors of 5: 1 (from 15) + 1 (from 5) = 2 factors of 5
The number of zeros is determined by the smaller number of factors of 2 and 5, which is 2.
3. A Special Implication
- While solving 45!, 46!, 47!, 48!, 49!. Notice the number of zeroes in each of the cases will be equal to 10.
- It is not difficult to understand that the number of fives in any of these factorials is equal to 10. The number of zeroes will only change at 50! (It will become 12).
- In fact, this will be true for all factorial values between two consecutive products of 5.
- Thus, 50!, 51!, 52!, 53! And 54! will have 12 zeroes (since they all have 12 fives). Similarly, 55!, 56!, 57!, 58! And 59! will each have 13 zeroes.
- While there are 10 zeroes in 49! There are 12 zeroes directly in 50!. This means that there is no value of a factorial which will give 11 zeroes. This occurs because to get 50! we multiply the value of 49! by 50. When you do so, the result is that we introduce two 5’s in the product. Hence, the number of zeroes jumps by two.
- Note: at 124! you will get 24 + 4 fi 28 zeroes. At 125! you will get 25 + 5 + 1 = 31 zeroes. (A jump of 3 zeroes.)
For example, n! has 13 zeroes. The highest and least values of n are?
(a) 57 and 58
(b) 59 and 55
(c) 59 and 6
(d) 79 and 55
Ans: (b)
Sol: For 13 trailing zeros, we find n! where the number of 5s (and multiples of 5) is 13.Using the formula:
The number of 5s is calculated by the sum: n/5 + n/25 + n/125 + ... (where we take integer parts).
For n = 55:
55/5 = 11 (multiples of 5)
55/25 = 2 (multiples of 25)
Total = 11 + 2 = 13 trailing zeros
Since we know that 50! is 12 zeroes so till 54! we will have 12 zeroes. Thus, 55 to 59! will have 13 zeroes.
Find the number of zeroes in the product 11x 22 x 33 x ...x 4949
Solved Examples
Q1: Find the last digit of 55552345 + 66665678
(a) 1
(b) 3
(c) 5
(d) 7
Ans: a
Sol: As the last digit depends only on last digits, consider the powers only for last digits, that is 52345 + 65678 .
As we know, any power of 5 ends only with 5 and any power of 6 ends only with 6.
The last digit of 52345 + 65678 = 5 + 6 = 11 = 1
Hence, option (A) is the correct answer.
Q2: If in a two digit number, the digit at the unit place is z and the digit at the tens place is 8, then the number is
(a) 80z + z
(b) 80 + z
(c) 8z + 8
(d) 80z + 1
Ans: (b)
Sol: Digit at unit’s place = z
The digit at ten’s place = 8
= 2-digit number = (10×8)+(1×z)
= 80 + z
Q3: How many trailing zeroes (zeroes at the end of the number) does 60! have?
(a) 14
(b) 12
(c) 10
(d) 8
Ans: (a)
Sol: The number of trailing zeroes in the decimal representation of a number = highest power of 10 that can divide the number.
For instance,
3600 = 36 * 102
45000 = 45 * 103In order to approach this question, let us first see the smallest factorial that ends in a zero.
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
Now, 5! ends in a zero as we have get a product of 10 when we compute 1 * 2 * 3 * 4 * 5.
10 is 2 * 5, so we get a factor of 10 every time we get a 2 and a 5 in the factorial.
So, 5! has 1 zero. The factorial that ends with 2 zeroes is 10!
15! has 3 zeroes.
20! has 4 zeroes and so on.
An extra zero is created every time a 2 and 5 combine. Every even number gives a two, while every fifth number gives us a 5.Now, the critical point here is that since every even number contributes at least a 2 to the factorial, 2 occurs way more frequently than 5. So, in order to find the highest power of 10 that can divide a number, we need to count the highest power of 5 that can divide that number. We do not need to count the number of 2’s in the system as there will be more than 2’s than 5’s in any factorial.
Now, every multiple of 5 will add a zero to the factorial. 1 * 2 * 3 *.......59 * 60 has twelve multiples of 5. So, it looks like 60! will end in 12 zeroes. But we need to make one more adjustment here.
25 is 52, so 25 alone will contribute two 5’s, and therefore add two zeroes to the system. Likewise, any multiple of 25 will contribute an additional zero.
So, 20! has 4 zeroes, 25! has 6 zeroes.
60! will have [60/5] zeroes arising due to the multiples of and an additional [60/25] due to the presence of 25 and 50.
{We retain only the integer component of [60/25] as the decimal part has no value}So, 60! will end with 12 + 2 zeros. = 14 zeros.
In general, any n! will end with
zeroes.
Generalizing further, in case we want to find the highest power of 3 that divides n!, this is nothing but
The highest power of 7 that divides n! is
In case of a composite number, we need to break into the constituent primes and compute the highest power that divides the number.
For instance, if we want to find the largest power of 15 that divides n!, this will be driven by the highest powers of 3 and 5 that divide n!. Similar to the scenario we saw with trailing zeroes, we can observe that there will definitely be at least as many 3’s than 5’s in any factorial. So, the highest power of 15 that divides n! is simply [n/5] + [n/25] + [n/125] + [n/625]............
Hence the answer is "14"
Q4: The number of zeros at the end of the product of 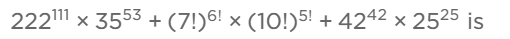
(a) 42
(b) 53
(c) 1055
(d) None of these
Ans: (a)
Sol: The number of zeros at the end of 222111 × 35 53 is 53.
The number of zeros at the end of (7!)6!×(10!)5! is 960.
The number of zeros at the end of 4242×2525 is 42.
Thus the number of zeros at the end of the whole expression is 42.
|
164 videos|630 docs|1142 tests
|
FAQs on Important Concepts: Number System - 2 - General Test Preparation for CUET UG - CUET Commerce
| 1. What is the unit digit of a number and how is it determined? |  |
| 2. What is the cyclicity table and how is it used in determining unit digits? |  |
| 3. How can the number of zeroes in a number be determined? |  |
| 4. Can the unit digit of a number be determined without calculating the entire number? |  |
| 5. Why is it important to understand the concept of unit digits in number systems? |  |