Chapter 4 - Quadratic Equations, RD Sharma Solutions - (Part-2) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Q.36. Solve the following quadratic equations by factorization:
x2−(√3+1)x+√3=0
Ans.
Consider the equation
x2−(√3+1)x+√3 = 0
⇒x2−(√3+1)x+√3 = 0
⇒x2−√3x−x+√3 = 0
⇒x(x−√3)−1(x−√3) = 0
⇒(x−√3)(x−1) = 0
⇒(x−√3)=0 or (x−1) = 0
⇒x = √3 or x = 1
Q.37. Solve the following quadratic equations by factorization:
3√5x2+25x−10√5=0
Ans.
Consider the equation
3√5x2+25x−10√5=0
⇒ 3√5x2+30x−5x−10√5 = 0
⇒ 3√5x(x+2√5)−5(x+2√5)=0
⇒ (3√5x−5)(x+2√5)=0
⇒ (3√5x−5)=0 or (x+2√5)=0
⇒ x=√5/3 or x=−2√5
Q.38. Solve the following quadratic equations by factorization:
√3x2−2√2x−2√3=0
Ans.
√3x2−2√2x−2√3=0
⇒√3x2−3√2x+√2x−2√3=0
⇒√3x(x−√6)+√2(x−√6)=0
⇒(√3x+√2)(x−√6)=0
⇒√3x+√2=0 or x−√6=0
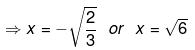
Hence, the factors are 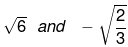
Q.39. Solve the following quadratic equations by factorization:
4√3x2+5x−2√3 = 0
Ans.
4√3x2+5x−2√3 = 0
4√3x2 + 8x - 3x - 2√3 = 0
4x(√3x+2) - √3(√3x+2) = 0
(√3x+2) (4x - √3) = 0
Therefore,
√3x + 2 = 0
√3x = -2
x = -2/√3
or,
4x - √3 = 0
4x = √3
x = √3/4
Hence
x = -2/√3 or x = √3/4
Q.40. Solve the following quadratic equations by factorization:
√2x2−3x−2√2=0
Ans.
We have been given
√2x2−3x−2√2 = 0
√2x2-4x+x- 2√2 = 0
√2x(x - 2√2) +1(x - 2√2) = 0
(x - 2√2)(√2x +1) = 0
Therefore,
x - 2√2 = 0
x = 2√2
or,
√2x+1 = 0
√2x = -1
x = -1/√2
Hence,
x = 2√2 or x = -1/√2
Q.41. Solve the following quadratic equations by factorization:
x2−(√2+1)x+√2=0
Ans.
Consider the equation
x2−(√2+1)x+√2 = 0
⇒ x2−√2x−x+√2 = 0
⇒ x(x−√2)−1(x−√2) = 0
⇒ (x−1)(x−√2) = 0
⇒ x−1=0 or x−√2 = 0
⇒ x=1 or x=√2
Q.42. Solve the following quadratic equations by factorization:
3x2−2√6x+2 = 0
Ans.
We have been given
3x2−2√6x+2 = 0
3x2 - √6x - √6x + 2 = 0
√3x(√3x - √2) - √2(√3x - √2) = 0
(√3x - √2)(√3x - √2) = 0
Therefore,
√3x - √2 = 0
√3x = √2
x = √2/√3
or,
√3x - √2 = 0
√3x = √2
x = √2/√3
Hence
x = √2/√3
Q.43. Find the roots of the quadratic equation √2x2+7x+5√2=0
Ans.
We write, 7x=5x+2x as √2x2×5√2=10x2=5x × 2x
∴ √2x2+7x+5√2 = 0
⇒ √2x2+5x+2x+5√2 = 0
⇒ x(√2x+5)+√2(√2x+5) = 0
⇒ (√2x+5)(x+√2) = 0
⇒ x+√2=0 or √2x+5 = 0
⇒ x = - √2 or x = -5/√2 = -5√2/√2
Hence, the roots of the given equation are - √2 and -5√2/√2.
Q.44. Solve the following quadratic equations by factorization: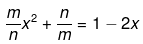
Ans.
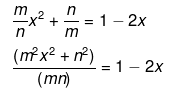
m2x2 + 2mnx + (n2 - mx) = 0
m2x2+mnx+mnx+[n2−(√mn)2] = 0
m2x2+mnx+mnx+(n+√mn)(n−√nm)+(m√mnx − m√mnx) = 0
[m2x2 + mnx + m√mn] + [mnx - m√mnx + (n + √mn)(n-√mn)] = 0
[m2x2 + mnx + m√mnx] +[(ms)(n - √mn)+(n+√mn)(n-√mn)] = 0
(mx) (mx +n+√mn) + (n-√mn)(mx+n+√mn) = 0
(mx+n+√mn)(mx+n-√mn) = 0
Therefore,
mx+n+√mn = 0
mx = -n -√mn
x - (-n -√mn)/m
or,
mx+n-√mn = 0
mx = -n+√mn
x = (-n+√mn)/m
Hence,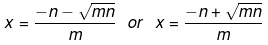
Q.45. Solve the following quadratic equations by factorization: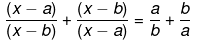
Ans.
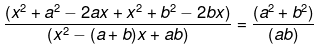
2abx2 - 2(ab)(a+b)x + ab(a2+b2) = (a2 + b2)x2 - (a+b) (a2+b2)x+ab(a2+b2)
(a-b)2x2 - (a+b)(a-b)2x = 0
x(a-b)2(x-(a+b)) = 0
Therefore,
x(a-b)2 = 0
x = 0
or,
x- (a-b) = 0
x = a+b
Hence, x = 0 or x = a+b
Page No 4.21
Q.46. Solve the following quadratic equations by factorization: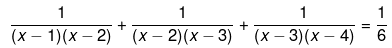
Ans.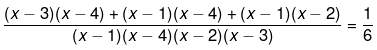
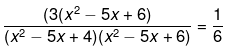
18 = x2 - 5x + 4
x2 - 5x - 14 = 0
x2 - 7x + 2x - 14 = 0
x(x - 7) + 2(x - 7) = 0
(x + 2)(x - 7) = 0
Therefore,
x + 2 = 0
x = -2
or,
x - 7 = 0
x = 7
Hence, x = -2 or x = 7.
Q.47. Solve the following quadratic equation by factorization: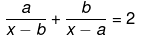
Ans.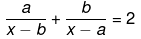
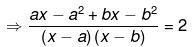
⇒ ax−a2+bx−b2 = 2x2−2bx−2ax+2ab
⇒ 2x2−2bx−2ax+2ab−ax+a2−bx+b2=0
⇒ 2x2+x[−2b−2a−a−b]+a2+b2+2ab=0
⇒ 2x2−3x[a+b]+(a+b)2=0
⇒ 2x2−2(a+b)x−(a+b)x+(a+b)2=0
⇒ 2x[x−(a+b)]−(a+b)[x−(a+b)]=0
⇒ [2x−(a+b)][x−(a+b)]=0
So, the value of x will be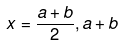
Q.48. Solve the following quadratic equations by factorization: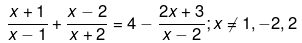
Ans.

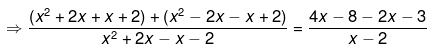
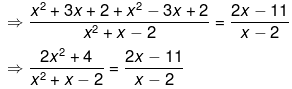
⇒ (2x2 + 4)(x - 2) = (2x - 11)( x2 + x - 2)
⇒ 2x3 - 4x2 + 4x - 8 = 2 x3 + 2x2 - 4x - 11x2 - 11x + 22
⇒ 2x3 - 4x2 + 4x - 8 = 2x3 - 9x2 - 15x + 22
⇒ 2x3 - 2x3 - 4x2 + 9x2 + 4x + 15x - 8 - 22 = 0
⇒ 5x2 + 19x - 30 = 0
⇒ 5x2 + 25x - 6x - 30 = 0
⇒ 5x(x + 5) - 6(x + 5) = 0
⇒ (5x - 6)(x + 5) = 0
⇒ 5x - 6 = 0, x + 5 = 0
⇒ x = 6/5 or x = -5
Q.49. Solve the following quadratic equations by factorization: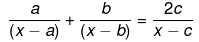
Ans.
We have been given,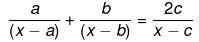
a(x - b)(x - c) + b(x - a)(x - c) = 2c(x - a)(x - b)
a(x2-(b + c)x + bc) + b(x2 - (a + c)x + ac) = 2c(x2 - (a + b)x + ab)
(a + b - 2c)x2 - (2ab - ac - bc)x = 0
x[(a + b - 2c)x - (2ab - ac - bc)] = 0
Therefore,
x = 0
or,
(a + b - 2c)x - (2ab - ac - bc) = 0
(a + b - 2c)x = (2ab - ac - bc)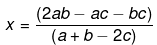
Hence,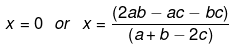
Q.50. Solve the following quadratic equations by factorization:
x2 + 2ab = (2a + b)x
Ans.
We have been given
x2 + 2ab = (2a + b)x
x2 - (2a + b)x + 2ab = 0
x2 - 2ax - bx + 2ab = 0
x(x - 2a) - b(x - 2a) = 0
(x - 2a)(x - b) = 0
Therefore,
x - 2a = 0
x = 2a
or,
x - b = 0
x = b
Hence,
x = 2a or x = b
Q.51. Solve the following quadratic equations by factorization:
a+b)2 x2-4abx-(a-b)2 = 0
Ans.
We have been given
(a + b)2x2 - 4abx - (a - b)2 = 0
(a + b)2x2 - (a + b)2x + (a - b)2x - (a - b)2 = 0
(a + b)2x(x - 1) + (a - b)2(x - 1) = 0
((a + b)2x + (a - b)2)(x - 1) = 0
Therefore,
(a + b)2x + (a - b)2 = 0
(a + b)2x = - (a - b)2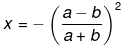
or,
x-1= 0
x = 1
Hence,
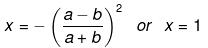
Q.52. Solve the following quadratic equations by factorization:
a(x2+1)−x(a2+1)=0
Ans.
We have been given
a(x2 + 1) - x(a2 + 1) = 0
ax2 - (a2 + 1)x + a = 0
ax2 - a2x - x + a = 0
ax(x - a) - 1(x - a) = 0
(ax - 1)(x - a) = 0
Therefore,
ax - 1 = 0
ax = 1
x = 1/a
or,
x - a = 0
x = a
Hence, x = 1/a or x = a
Q.53. Solve the following quadratic equations by factorization:
x2 − x − a(a + 1) = 0
Ans.
We have been given
x2 - x - a(a + 1) = 0
x2 + ax - (a + 1)x - a(a + 1) = 0
x(x + a) - (a + 1)(x + a) = 0
(x - (a + 1))(x + a) = 0
Therefore,
x - (a + 1) = 0
x = (a + 1)
or,
x + a = 0
x = -a
Hence,
x = a + 1 or x = -a
Q.54. Solve the following quadratic equations by factorization:
Ans.
We have been given
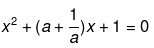
Therefore,
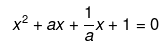
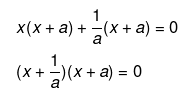
Therefore,
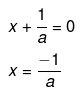
or,
x+a = 0
x = -a
Hence,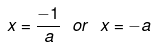
Q.55. Solve the following quadratic equations by factorization:
abx2+(b2−ac)x−bc=0
Ans.
We have been given
abx2 + (b2 - ac)x - bc = 0
abx2 + b2x - acx - bc = 0
bx(ax + b) - c(ax + b) = 0
(ax + b)(bx - c) = 0
Therefore,
ax + b = 0
ax = -b
x = -b/a
or,
bx-c = 0
bx = c
x = c/b
Hence,
x = -b/a or x = c/b
Q.56. Solve the following quadratic equations by factorization:
a2b2x2 + b2x - a2x - 1 = 0
Ans.
We have been given
a2b2x2 + b2x - a2x - 1 = 0
b2x(a2x + 1) - 1(a2x + 1) = 0
(b2x - 1)(a2x + 1) = 0
Therefore,
b2x - 1 = 0
b2x = 1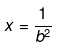
or,
a2x + 1 = 0
a2x = -1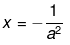
Hence,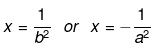
Q.57. Solve the following quadratic equations by factorization: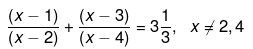
Ans.
We have been give
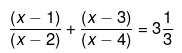
3(x2 - 5x + 4 + x2 - 5x + 6) = 10(x2 - 6x + 8)
4x2 - 30x + 50 = 0
2x2 - 15x + 25 = 0
2x2 - 10x - 5x + 25 = 0
2x(x - 5) - 5(x - 5) = 0
(2x - 5)(x - 5) = 0
Therefore,
2x - 5 = 0
2x = 5
x = 5/2
or,
x - 5 = 0
x = 5
Hence,
x = 5/2 or x = 5
Q.58. Solve the following quadratic equations by factorization: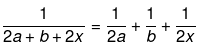
Ans.
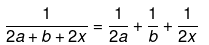
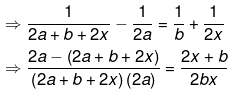
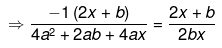
⇒ −2bx(2x+b)=(4a2+2ab+4ax)(2x+b)
⇒ (4a2+2ab+4ax)(2x+b)+2bx(2x+b) = 0
⇒ (2x+b)(4a2+2ab+4ax+2bx) = 0
⇒ 2x+b=0 or 4a2+2ab+(4a+2b)x = 0

Hence, the factors are x = -a or x = -b/2
Q.59. Solve the following quadratic equations by factorization: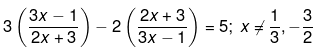
Ans.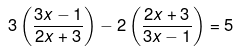
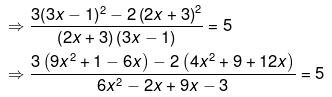
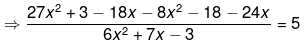
⇒19x2−42x−15=5(6x2+7x−3)
⇒19x2−42x−15=30x2+35x−15
⇒30x2−19x2+35x+42x−15+15 = 0
⇒11x2+77x = 0
⇒x2+7x = 0
⇒x(x+7) = 0
⇒x = 0 or x+7 = 0
⇒x = 0 or x = −7
Hence, the factors are 0 and −7.
Q.60. Solve the following quadratic equations by factorization: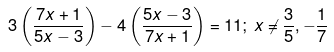
Ans.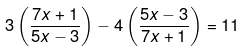
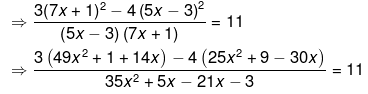
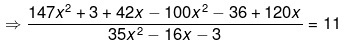
⇒ 47x2+162x−33 = 11(35x2−16x−3)
⇒ 47x2+162x−33 = 385x2−176x−33
⇒ 385x2−47x2−176x−162x−33+33 = 0
⇒ 338x2−338x=0
⇒ x2−x=0
⇒ x(x−1)=0
⇒ x = 0 or x−1 = 0
⇒ x = 0 or x = 1
Hence, the factors are 0 and 1.
Q.61. Solve the following quadratic equations by factorization: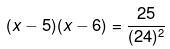
Ans.
We have been given that,
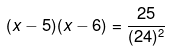
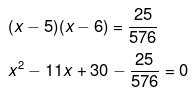
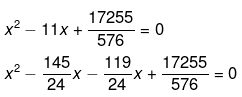
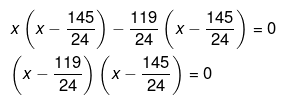
Therefore,
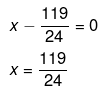
or
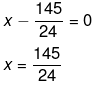
Hence,
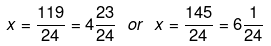
Q.62. Solve the following quadratic equations by factorization: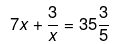
Ans.
We have been given,
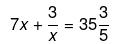
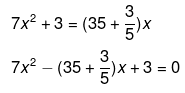
Therefore,

or,
x - 5 = 0
x = 5
Hence,
x = 3/35 or x = 5
Page No 4.26
Q.1. Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
x2−4√2x+6=0
Ans.
We have been given that,
x2−4√2x+6=0
Now we take the constant term to the right hand side and we get
x2−4√2x = −6
Now add square of half of co-efficient of ‘x’ on both the sides. We have,
2−4√2x+(2√2)2=(2√2)2−6
x2+(2√2)2−2(2√2)x=2
(x−2√2)2=2
Since right hand side is a positive number, the roots of the equation exist.
So, now take the square root on both the sides and we get
x−2√2=±√2
x=2√2 ± √2
Now, we have the values of ‘x’ as
x=2√2+√2
=3√2
Also we have,
x=2√2−√2
=√2
Therefore the roots of the equation are 3√2 and √2.
Q.2. Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
2x2 − 7x + 3 = 0
Ans.
We have to find the roots of given quadratic equation by the method of completing the square. We have,
2x2 − 7x + 3 = 0
We should make the coefficient of x2 unity. So,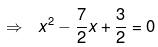
Now shift the constant to the right hand side,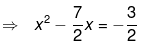
Now add square of half of coefficient of x on both the sides,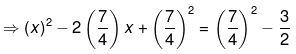
We can now write it in the form of perfect square as,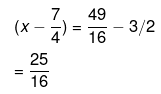
Taking square root on both sides,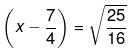
So the required solution of,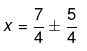
= 3, 1/2
Q.3. Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
3x2 + 11x + 10 = 0
Ans.
We have been given that,
3x2 + 11x + 10 = 0
Now divide throughout by 3. We get,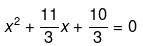
Now add square of half of co-efficient of ‘x’ on both the sides. We have,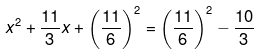
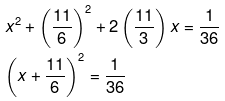
Since RHS is a positive number, therefore the roots of the equation exist.
So, now take the square root on both the sides and we get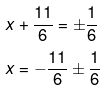
Now, we have the values of ‘x’ as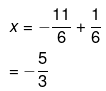
Also we have,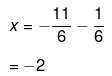
Therefore the roots of the equation are -2 and -5/3.
Q.4. Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
2x2 + x − 4 = 0
Ans.
We have been given that,
2x2 + x − 4 = 0
Now divide throughout by 2. We get,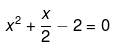
Now take the constant term to the RHS and we get 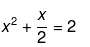
Now add square of half of co-efficient of ‘x’ on both the sides. We have,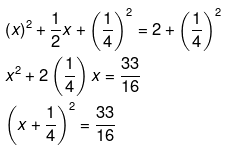
Since RHS is a positive number, therefore the roots of the equation exist.
So, now take the square root on both the sides and we get
Now, we have the values of ‘x’ as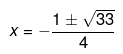
Also we have,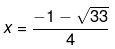
Therefore the roots of the equation are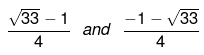
FAQs on Chapter 4 - Quadratic Equations, RD Sharma Solutions - (Part-2) - RD Sharma Solutions for Class 10 Mathematics
| 1. How to solve quadratic equations using the quadratic formula? |  |
| 2. What are the different methods to solve quadratic equations? |  |
| 3. How can we determine the nature of roots of a quadratic equation without solving it? |  |
| 4. What is the relationship between the coefficients of a quadratic equation and the sum and product of its roots? |  |
| 5. Can a quadratic equation have no real roots? |  |






















