Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-13) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 3.45
Q.27. Solve the following systems of equations: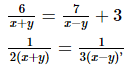
where x + y ≠ 0 and x − y ≠ 0
Ans. The given equations are: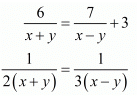
Let 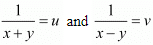 then equations are
then equations are
6u = 7v + 3 ...(i)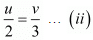
Multiply equation (ii) b 12 and subtract (ii) from (i), we get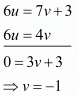
Put the value of v in equation (i), we get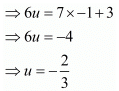
Then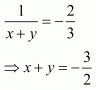
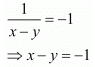
Add both equations, we get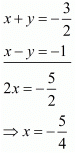
Put the value of x in second equation, we get
6 x 2 + 6y = 5 x 2y
⇒ 12 = 4y
Hence the value of 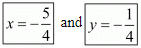
Q.28. Solve the following systems of equations: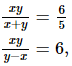
where x + y ≠ 0, y − x ≠ 0
Ans. The given equations are: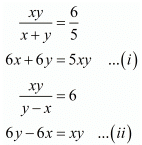
Add both equations, we get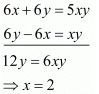
Put the value of x in equation (i), we get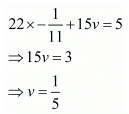
Hence the value of x = 2 and y = 3
Q.29. Solve the following systems of equations: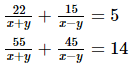
Ans. The given equations are: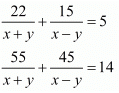
Let 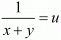 and
and 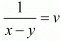 then equations are
then equations are
22u + 15v = 5 ...(i)
55u + 45v = 14 ...(ii)
Multiply equation (i) by 3 and subtracting (ii) from (i), we get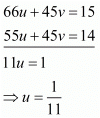
Put the value of u in equation (i), we get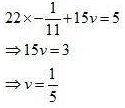
Then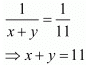
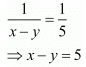
Add both equations, we get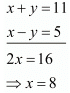
Put the value of x in second equation, we get
8 - y = 5
⇒ - y = -3
Hence the value of x = 8 and y = 3
Q.30. Solve the following systems of equations: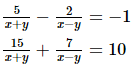
Ans. The given equations are: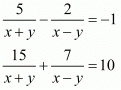
Let 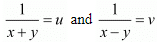 then equations are
then equations are
5u - 2v = - 1 ...(i)
15u + 7v = 10 ...(ii)
Multiply equation (i) by 7 and equation (ii) by 2 and add both equations, we get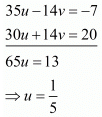
Put the value of u in equation (i), we get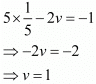
Then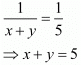

Add both equations, we get
Put the value of x in first equation, we get
3 + y = 5
⇒ y = 2
⇒ y = 2
Hence the value of x = 3 and y = 2.
Q.31. Solve the following systems of equations: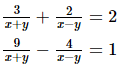
Ans. The given equations are: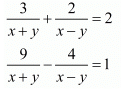
Let 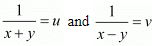 then equations are
then equations are
3u + 2v = 2 ...(i)
9u - 4v = 1 ...(ii)
Multiply equation (i) by 2 and add both equations, we get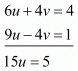
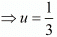
Put the value of u in equation (i), we get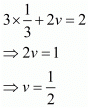
Then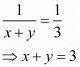
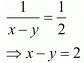
Add both equations, we get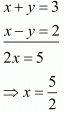
Put the value of x in first equation, we get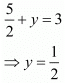
Hence the value of 
Q.32. Solve the following systems of equations: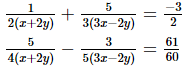
Ans. The given equations are: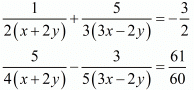
Let 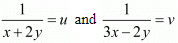 then equations are
then equations are
Multiply equation (i) by 3/5 and equation (ii) by 5/3 add both equations, we get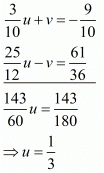
Put the value of u in equation (i), we get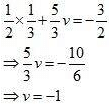
Then
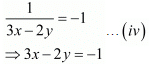
Add both equations, we get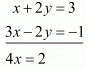
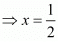
Put the value of x in equation (iii) we get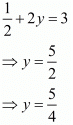
Hence the value of 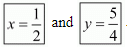
Page No 3.46
Q.33. Solve the following systems of equations: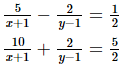
where x ≠ −1 and y ≠ 1
Ans. The given equations are: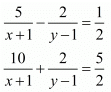
Let 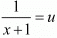 and
and  then equations are
then equations are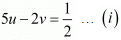
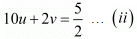
Add both equations, we get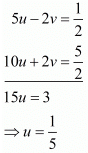
Put the value of u in equation (i), we get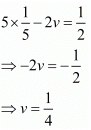
Then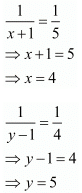
Hence the value of x = 4 and y = 5.
Q.34. Solve the following systems of equations:
x + y = 5xy
3x + 2y = 13xy,
x ≠ 0, y ≠ 0
Ans. The given equations are:
x + y = 5 xy ...(i)
3x + 2y = 13xy ...(ii)
Multiply equation (i) by 2 and subtract (ii) from (i), we get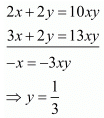
Put the value of y in equation (i), we get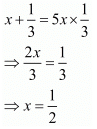
Hence the value of 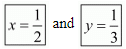
Q.35. Solve the following systems of equations: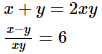
x ≠ 0, y ≠ 0
Ans. The given equations are:
x + y = 2xy ...(i)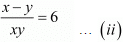
x - y = 6xy
Add both equations we get
Put the value of y in equation (i), we get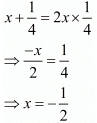
Hence the value of 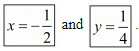
Q.36. Solve the following systems of equations:
2(3u − ν) = 5uν
2(u + 3ν) = 5uν
Ans. The given equations are: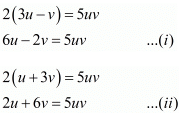
Multiply equation (i) by 3 and add both equations, we get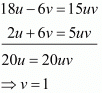
Put the value of v in equation (i), we get
6u - 2 x 1 = 5u x 1
⇒ u = 2
Hence the value of u = 2 and v = 1.
Q.37. Solve the following systems of equations: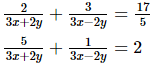
Ans. The given equations are: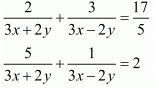
Let 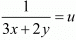 and
and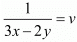 then equations are
then equations are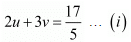
5u + v = 2 ...(ii)
Multiply equation (ii) by 3 and subtract (ii) from (i), we get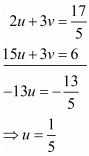
Put the value of u in equation (i), we get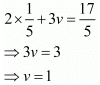
Then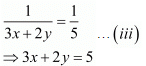
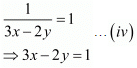
Add both equations, we get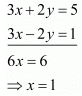
Put the value of x in equation (iii) we get
3 x 1 + 2y = 5
⇒ 2y = 2
⇒ y = 1
Hence the value of x = 1 and y = 1
Q.38. Solve the following systems of equations: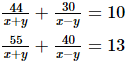
Ans. The given equations are: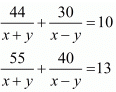
Let 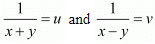 then equations are
then equations are
44u + 30v = 10 ...(i)
55u + 40v = 13 ...(ii)
Multiply equation (i) by 4 and equation (i) by 3 add both equations, we get
Put the value of u in equation (i), we get
Then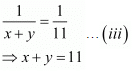
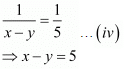
Add both equations, we get
Put the value of x in equation (iii) we get
8 x 1 + y = 11
⇒ y = 3
Hence the value of x = 8 and y = 3
Q.39. Solve the following systems of equations: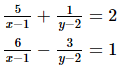
Ans. The given equations are: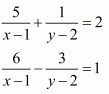
Let 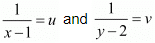 then equations are
then equations are
5u + v = 2 ...(i)
6u - 3v = 1 ...(ii)
Multiply equation (i) by 3 and add both equations, we get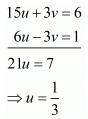
Put the value of u in equation (i), we get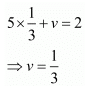
Then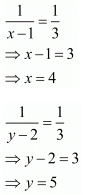
Hence the value of x = 4 and y = 5.
Page No 3.46
Q.40. Solve the following systems of equations: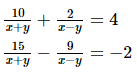
Ans. The given equations are: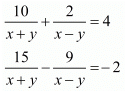
Let 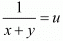 and
and 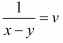 then equations are
then equations are
10u + 2v = 4 ...(i)
15u - 9v = - 2 ...(ii)
Multiply equation (i) by 9 and equation (ii) by 2 and add both equations, we get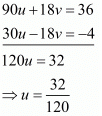
Put the value of u in equation (i), we get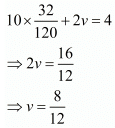
Then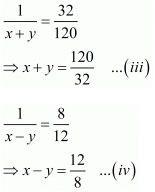
Add both equations, we get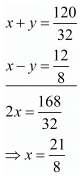
Put the value of x in equation (iii) we get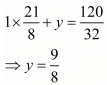
Hence the value of 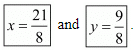
Q.41. Solve the following systems of equations: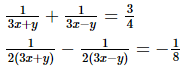
Ans. The given equations are: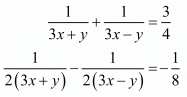
Let  and
and 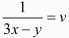 then equations are
then equations are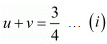
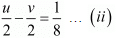
Multiply equation (ii) by 2 and add both equations, we get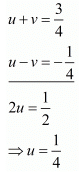
Put the value of u in equation (i), we get
Then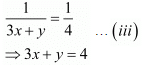
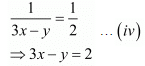
Add both equations, we get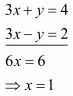
Put the value of x in equation (iii) we get
3 x 1 + y = 4
⇒ y = 1
Hence the value of x = 1 and y = 1
Q.42. Solve the following systems of equations: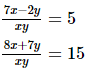
Ans. The given equations are: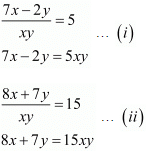
Multiply equation (i) by 7 and equation (ii) by 2, add both equations we get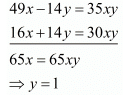
Put the value of y in equation (i), we get
7x - 2 x 1 = 5x x 1
⇒ 2x = 2
⇒ x = 1
Hence the value of x = 1 and y = 1
Q.43. Solve the following systems of equations:
152x − 378y = −74
−378x + 152y = −604
Ans. The given equations are:
152x − 378y = −74 ...(i)
−378x + 152y = −604 ...(ii)
Multiply equation (i) by 152 and equation (ii) by 378 and add both equations we get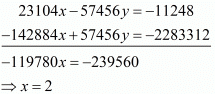
Put the value of x in equation (i), we get
152 x 2 - 378y = -74
⇒ - 378y = - 378
⇒ y = 1
Hence the value of x = 2 and y = 1
Q.44. Solve the following systems of equations:
99x + 101y = 499
101x + 99y = 501
Ans. The given equations are:
99x + 101y = 499 ...(i)
101x + 99y = 501 ...(ii)
Multiply equation (i) by 99 and equation (ii) by, and subtract (ii) from (i) we get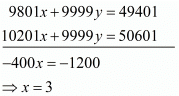
Put the value of x in equation (i), we get
99 x 3 + 101y = 499
⇒ 101y = 202
⇒ y = 2
Hence the value of x = 3 and y = 2
Q.45. Solve the following systems of equations:
23x − 29y = 98
29x − 23y = 110
Ans. The given equations are:
23x − 29y = 98 ...(i)
29x − 23y = 110 ...(ii)
Multiply equation (i) by 23 and equation (ii) by 29 and subtract (ii) from (i) we get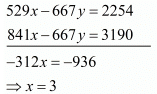
Put the value of x in equation (i), we get
23 x 3 - 29y = 98
⇒ - 29y = 29
⇒ y = - 1
Hence the value of x = 3 and y = - 1
Q.46. Solve the following systems of equations:
x − y + z = 4
x − 2y − 2z = 9
2x + y + 3z = 1
Ans. The given equations are:
x - y + z = 4 ...(i)
x − 2y − 2z = 9 ...(ii)
2x + y + 3z = 1 ...(iii)
First of all we find the value of x
x = 4 + y - z
Put the value of x in equation (ii), we get
4 + y - z - 2y - 2z = 9
⇒ - 3z - y = 5 ...(iv)
Put the value of x and y in equation in (iii) we get
2(4 + y - z) + y + 3z = 1
⇒ 8 + 2y - 2z + y + 3z = 1
⇒ 3y + z = - 7 ...(v)
Multiply equation (iv) by and add equations (iv) and (v), we get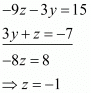
Put the value of z in equation (v), we get
3y - 1 = - 7
⇒ 3y = -6
⇒ y = - 2
Put the value of y and z in equation (i) we get
x - (-2) - 1 = 4
⇒ x = 3
Hence the value of x = 3, y = - 2 and z = - 1.
Q.47. Solve the following systems of equations:
x − y + z = 4
x + y + z = 2
2x + y − 3z = 0
Ans. The given equations are:
x - y + z = 4 ...(i)
x + y + z = 2 ...(ii)
2x + y - 3z = 0 ...(iii)
First of all we find the value of x
x = 4 + y- z
Put the value of x in equation (i), we get
4 + y - z + y + z = 2
⇒ 2y = - 2
⇒ y = - 1
Put the value of x and y in equation in (iii) we get
2(4 + y - z) + y - 3z = 0
⇒ 8 - 2 - 2z - 1 - 3z = 0
⇒ - 5z = -5
⇒ z = 1
Put the value of y and z in equation (i), we get
x - (-1) + 1 = 4
⇒ x = 2
Hence the value of x = 2, y = - 1 and z = 1
Q.48.
21x + 47y = 110
47x + 21y = 162
Ans.
21x + 47y = 110 .....(i)
47x + 21y = 162 .....(ii)
Adding (i) and (ii), we get
68x + 68y = 272
⇒x + y = 4 .....(iii)
Subtracting (i) from (ii), we get
26x −26y = 52
⇒ x − y = 2 .....(iv)
Adding (iii) and (iv), we get
2x = 6 ⇒ x = 3
Putting x = 3 in (iv), we get
3 − y = 2
⇒ y = 1
Q.49. If (x + 1) is a factor of 2x3 + ax2 + 2bx + 1, then find the values of a and b given that 2a − 3b = 4.
Ans. Since (x + 1) is a factor of 2x3 + ax2 + 2bx + 1, so
2(−1)3 + a(−1)2+2b(−1)+1=0
⇒ −2 + a −2b + 1 = 0
⇒ a − 2b − 1 = 0
⇒a − 2b = 1 .....(i)
Also, we are given
2a − 3b = 4 .....(ii)
From (i) and (ii) we get
a = 1 + 2b .....(iii)
Substituting the value of a in (ii), we get
2(1 + 2b) − 3b = 4
⇒2 + 4b − 3b = 4
⇒ b = 2
Putting b = 2 in (iii), we get
a = 1 + 2 × 2 = 5
Thus, the value of a = 5 and b = 2.
Q.50. Find the solution of the pair of equations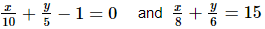 .
.
Hence , find λ, if y = λx + 5.
Ans. The given equations are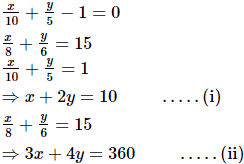
Multiplying (i) by 2, we get
2x + 4y = 20 .....(iii)
Subtracting (ii) from (iii), we get
x = 340
Putting x = 340 in (i), we get
340 + 2y = 10
⇒ 2y = 10 − 340 = −330
⇒ y = −165
Now, in order to find the value of λ, we simply put the value of x and y in the equation y = λx + 5.
∴ −165 = λ (340) + 5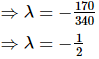
Thus, the value of λ =
Page No 3.47
Q.51. Find the values of x and y in the following rectangle.
Ans.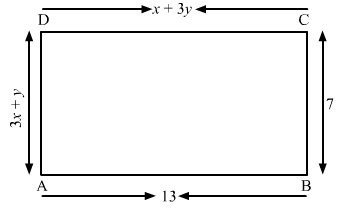
ABCD is the given rectangle. So, AB = CD and AD = BC.
Thus,
x + 3y = 13 .....(i)
3x + y = 7 .....(ii)
Adding (i) and (ii), we get
4x + 4y = 20
⇒x + y = 5 .....(iii)
Subtracting (i) from (ii), we get
2x − 2y = −6
⇒x − y = −3 .....(iv)
Adding (iii) and (iv), we get
2x = 2
⇒ x = 1
Putting x = 1 in (iii), we get
1 + y = 5
⇒ y = 4
Thus, x = 1 and y = 4.
Q.52. Write an equation of a line passing through the point representing solution of the pair of linear equations x + y =2 and 2x − y = 1 . How many such lines can we find ?
Ans. The given equations are
x + y = 2 .....(i)
2x − y = 1 .....(ii)
Adding (i) and (ii), we get
3x = 3
⇒ x = 1
Putting x = 1 in (i), we get
1 + y = 2
⇒ y = 1
Thus, the solution of the given equations is (1, 1).
We know that, infinitely many straight lines pass through a single point.
So, the equation of one such line can be 3x + 2y = 5 or 2x + 3y = 5.
FAQs on Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-13) - RD Sharma Solutions for Class 10 Mathematics
| 1. How can we solve a pair of linear equations in two variables using the elimination method? |  |
| 2. Can a pair of linear equations in two variables have infinitely many solutions? |  |
| 3. How can we determine if a pair of linear equations in two variables has a unique solution? |  |
| 4. What is the graphical method of solving a pair of linear equations in two variables? |  |
| 5. When can a pair of linear equations in two variables have no solution? |  |






















