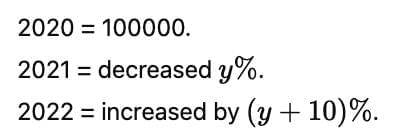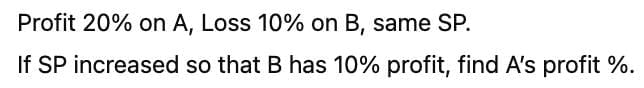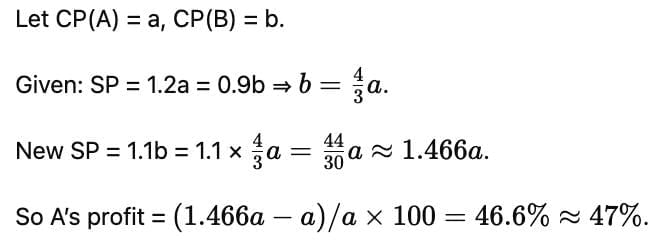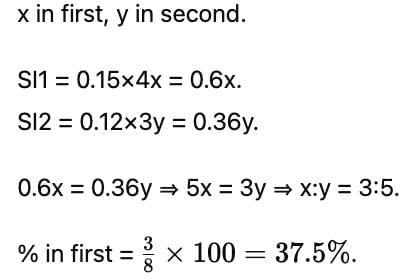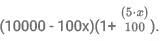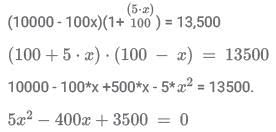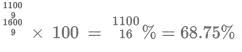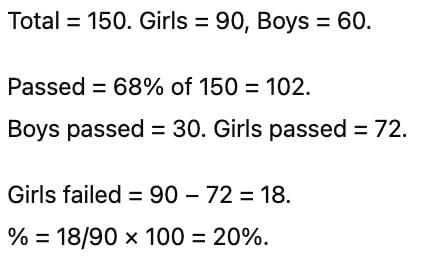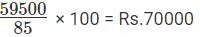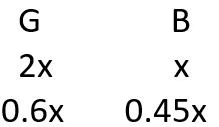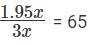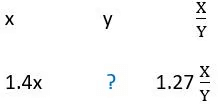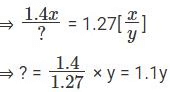Percentages CAT Previous Year Questions with Answer PDF
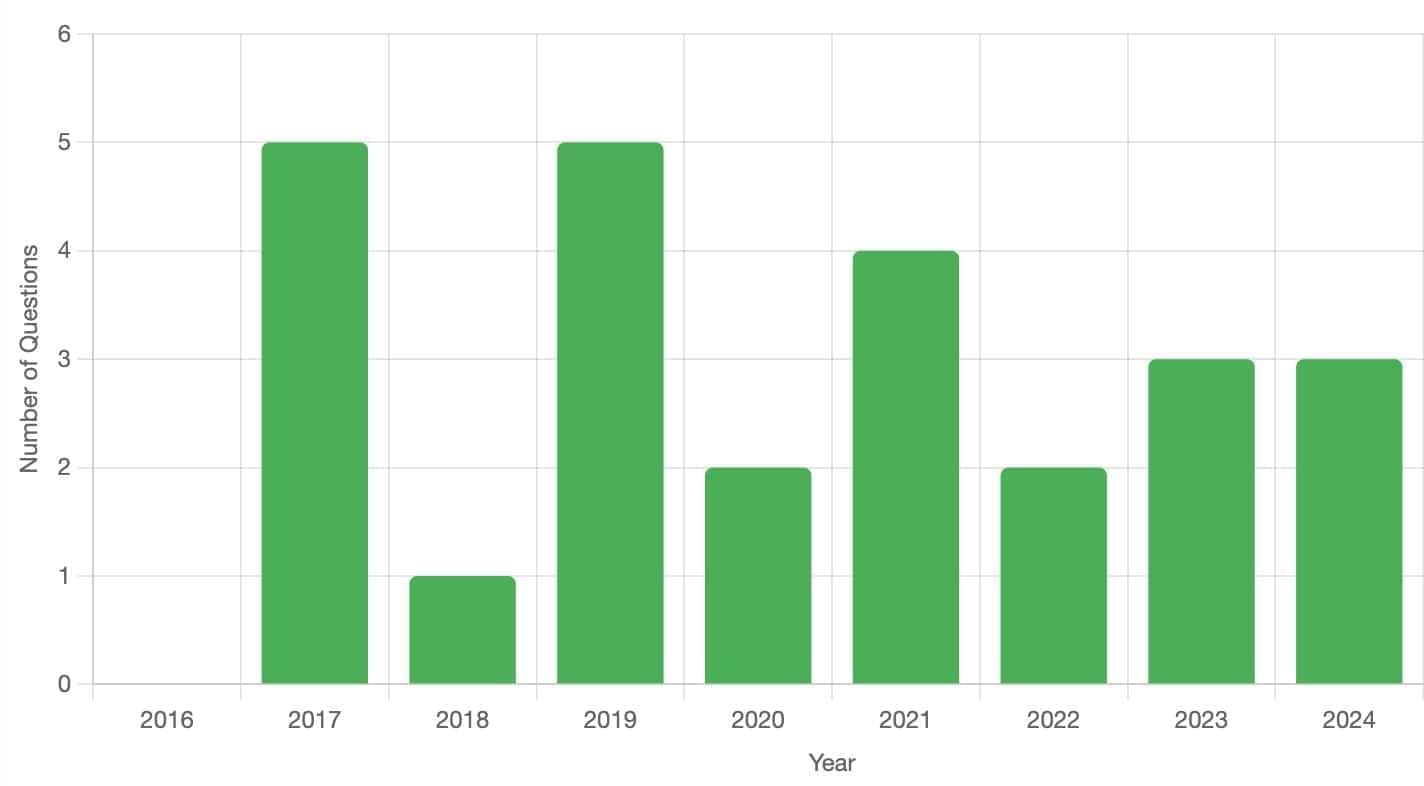
From 2016 to 2024, 25 percentage-based questions appeared in CAT Quant, usually 1–5 questions per year. They covered successive changes, profit/loss, population or salary hikes, and ratio derivations via alligation or algebra. Most were moderately difficult, focusing on multi-step calculations involving growth rates, scores, defects, exports, and investments.
2024
Q1: A fruit seller has a stock of mangoes, bananas and apples with at least one fruit of each type. At the beginning of a day, the number of mangoes make up 40% of his stock. That day, he sells half of the mangoes, 96 bananas and 40% of the apples. At the end of the day, he ends up selling 50% of the fruits. The smallest possible total number of fruits in the stock at the beginning of the day is
Ans: 340
Sol: Assume the total number of fruits = 5n.
So, the number of mangoes = (40/100)*5n = 2n.
Assume the number of apples = 5m.
He sold n mangoes, 96 bananas and 2m apples, which is equal to 50% of the total fruits.
n + 96 + 2m = 2.5n
2n + 192 + 4m = 5n
192 + 4m = 3n
The smallest value of m that will satisfy the equation is m = 3.
192 + 12 = 204 = 3n
n = 68
The smallest possible total number of fruits in the stock at the beginning of the day is 5n = 5*68 = 340.
Hence, 340 is the required answer
Q2: In a group of 250 students, the percentage of girls was at least 44% and at most 60%. The rest of the students were boys. Each student opted for either swimming or running or both. If 50% of the boys and 80% of the girls opted for swimming while 70% of the boys and 60% of the girls opted for running, then the minimum and maximum possible number of students who opted for both swimming and running, are
(a) 75 and 90, respectively
(b) 72 and 80, respectively
(c) 75 and 96, respectively
(d) 72 and 88, respectively
Ans: b
Sol: Total students = 250
Let’s take minimum Case-
The number of girls will be 44%
So Girls = 250 x 44/100 = 110
Boys = 140
In Girls 80% opted for swimming (S) and 60% for running (R)
Min number of girls doing both = 44
In Boys 50% opted for swimming (S) and 70% for running (R)
Min number of boys doing both = 28
So min number of students doing both activities = 44 + 28 = 72
Let’s take maximum Case-
The number of girls will be 60%
So Girls = 250 x 60/100 = 150
Boys = 100
In Girls 80% opted for swimming (S) and 60% for running (R)
Max number of girls doing both = 60In Boys 50% opted for swimming (S) and 70% for running (R)
Max number of boys doing both = 20
So max number of students doing both activities = 60 + 20 = 80
Hence, the minimum and maximum possible number of students who opted for both swimming and running, are 72 and 80, respectively.
Q3: After two successive increments, Gopal's salary became 187.5% of his initial salary. If the percentage of salary increase in the second increment was twice of that in the first increment, then the percentage of salary increase in the first increment was
(a) 30
(b) 25
(c) 27.5
(d) 20
Ans: b
Sol:
2023
Q1: The salaries of three friends Sita, Gita and Mita are initially in the ratio 5 : 6 : 7, respectively. In the first year, they get salary hikes of 20%, 25% and 20%, respectively. In the second year, Sita and Mita get salary hikes of 40% and 25%, respectively, and the salary of Gita becomes equal to the mean salary of the three friends. The salary hike of Gita in the second year is [2023]
(a) 26%
(b) 28%
(c) 25%
(d) 30%
Ans: a
Sol:Initial ratio = 5:6:7.
Year 1 hikes: S=20%, G=25%, M=20%.
Year 2: S +40%, M +25%, G’s salary = mean of three.
Q2: The population of a town in 2020 was 100000. The population decreased by y% from the year 2020 to 2021, and increased by x% from the year 2021 to 2022, where x and y are two natural numbers. If population in 2022 was greater than the population in 2020 and the difference between x and y is 10, then the lowest possible population of the town in 2021 was [2023]
(a) 74000
(b) 75000
(c) 72000
(d) 73000
Ans: d
Sol:
Q3: Gita sells two objects A and B at the same price such that she makes a profit of 20% on object A and a loss of 10% on object B. If she increases the selling price such that objects A and B are still sold at an equal price and a profit of 10% is made on object B, then the profit made on object A will be nearest to
(a) 42%
(b) 47%
(c) 45%
(d) 49%
Ans: b
Sol:
2022
Q1: In an election, there were four candidates and 80% of the registered voters casted their votes. One of the candidates received 30% of the casted votes while the other three candidates received the remaining casted votes in the proportion 1 : 2 : 3. If the winner of the election received 2512 votes more than the candidate with the second highest votes, then the number of registered voters was: [2022]
(a) 60288
(b) 50240
(c) 40192
(d) 62800
Ans: d
Sol:
Let the total number of registered voters be 100x.
Number of votes casted = 80xVotes for Candidate 1 = 30% of 80x = 24x
∴ Remaining three candidates will recieve = 80x - 24x = 56x votes.Remaining 3 candidates get votes in the ratio of 1 : 2 : 3 of the remaining 56x votes.
⇒ Votes of Candidate 2 = 1/6 × 56x = 28x/3
⇒ Votes of Candidate 3 = 2/6 × 56x = 56x/3
⇒ Votes of Candidate 4 = 3/6 × 56x = 28xHighest number of votes is received by Candidate 4 while second highest is by Candidate 1.
⇒ 28x – 24x = 2512
⇒ x = 2512/4 = 628∴ total number of registered votes = 100x = 62800
Hence, option (d).
Q2: Alex invested his savings in two parts. The simple interest earned on the first part at 15% per annum for 4 years is the same as the simple interest earned on the second part at 12% per annum for 3 years. Then, the percentage of his savings invested in the first part is
(a) 37.5%
(b) 60%
(c) 62.5%
(d) 40%
Ans: a
Sol:
2021
Q1: Raj invested ₹ 10000 in a fund. At the end of first year, he incurred a loss but his balance was more than ₹ 5000. This balance, when invested for another year, grew and the percentage of growth in the second year was five times the percentage of loss in the first year. If the gain of Raj from the initial investment over the two year period is 35%, then the percentage of loss in the first year is
(a) 5
(b) 15
(c) 17
(d) 10
Ans: d
Sol: Raj invested Rs 10000 in the first year. Assuming the loss he faced was x%.
The amount after 1 year is 10,000*(1 - x/100). = 10000 - 100*x.
Given the balance was greater than Rs 5000 and hence x < 50 percent.
When Raj invested this amount in the second year he earned a profit which is five times that of the first-year percentage.
Hence the amount after the second year is :Raj gained a total of 35 percent over the period of two years and hence the 35 percent is Rs 3500.
Hence the final amount is Rs 13,500.Solving the equation the roots are :
x = 10, x = 70.
Since x < 50, x = 10 percent.
Q2: Identical chocolate pieces are sold in boxes of two sizes, small and large. The large box is sold for twice the price of the small box. If the selling price per gram of chocolate in the large box is 12% less than that in the small box, then the percentage by which the weight of chocolate in the large box exceeds that in the small box is nearest to [2021]
(a) 144
(b) 127
(c) 135
(d) 124
Ans: b
Sol:
Q3: In a tournament, a team has played 40 matches so far and won 30% of them. If they win 60% of the remaining matches, their overall win percentage will be 50%. Suppose they win 90% of the remaining matches, then the total number of matches won by the team in the tournament will be
(a) 80
(b) 78
(c) 84
(d) 86
Ans: c
Sol:
Q4: The total of male and female populations in a city increased by 25% from 1970 to 1980. During the same period, the male population increased by 40% while the female population increased by 20%. From 1980 to 1990, the female population increased by 25%. In 1990, if the female population is twice the male population, then the percentage increase in the total of male and female populations in the city from 1970 to 1990 is
(a) 68.25
(b) 68.75
(c) 68.50
(d) 69.25
Ans: b
Sol: Let us solve this question by assuming values(multiples of 100) and not variables(x).
Since we know that the female population was twice the male population in 1990, let us assume their respective values as 200 and 100.
Note that while assuming numbers, some of the population values might come out as a fraction(which is not possible, since the population needs to be a natural number). However, this would not affect our answer, since the calculations are in ratios and percentages and not real values of the population in any given year.Now, we know that the female population became 1.25 times itself in 1990 from what it was in 1980.
Hence, the female population in 1980 = 200/1.25 = 160
Also, the female population became 1.2 times itself in 1980 from what it was in 1970.
Hence, the female population in 1970 = 160/1.2 = 1600/12 = 400/3Let the male population in 1970 be x. Hence, the male population in 1980 is 1.4x.
Now, the total population in 1980 = 1.25 times the total population in 1970.
Hence, 1.25 (x + 400/3) = 1.4x + 160
Hence, x = 400/9.
Population change = 300 - 400/9 - 400/3 = 300 - 1600/9 = 1100/9
percentage change =
2020
Q1: In a group of people, 28% of the members are young while the rest are old. If 65% of the members are literates, and 25% of the literates are young, then the percentage of old people among the illiterates is nearest to [2020]
(a) 62
(b) 55
(c) 66
(d) 59
Ans: c
Sol:
Q2: In May, John bought the same amount of rice and the same amount of wheat as he had bought in April, but spent ₹ 150 more due to price increase of rice and wheat by 20% and 12%, respectively. If John had spent ₹ 450 on rice in April, then how much did he spend on wheat in May? [2020]
(a) ₹ 580
(b) ₹ 570
(c) ₹ 560
(d) ₹ 590
Ans: c
Sol:
Amount spent on rice in May = 450 x 1.2 = ₹ 540.
If the amount spent on wheat in April is w, then in May it would be 1.12w.
Given, (1.12w + 540) - (w + 450) = 150
⇒ 12w = 60
⇒ w = 500
∴ The amount spent on wheat in May = 1.12w i.e., 560
2019
Q1: The income of Amala is 20% more than that of Bimala and 20% less than that of Kamala. If Kamala's income goes down by 4% and Bimala's goes up by 10%, then the percentage by which Kamala's income would exceed Bimala's is nearest to [2019]
(a) 28
(b) 29
(c) 31
(d) 32
Ans: c
Sol:
Q2: Meena scores 40% in an examination and after review, even though her score is increased by 50%, she fails by 35 marks. If her post-review score is increased by 20%, she will have 7 marks more than the passing score. The percentage score needed for passing the examination is [2019]
(a) 75
(b) 80
(c) 60
(d) 70
Ans: d
Sol:
Let total maximum marks in the examination = 100XMeena’s score = 40% of 100X = 40X
Meena’s marks after review = 40X + 50% of 40X
⇒ 40X + 20X = 60X
With 60x score, she fails by 35 marks. So, passing marks = 60x + 35
Meena’s marks after post review = 60X + 20% of 60X
⇒ 60X + 12X = 72X
Now, passing score = 72X – 7
Equating equation (i) and (ii) we get,
⇒ 72X – 7 = 60X + 35
⇒ 12X = 42
⇒ X = 7/2
Percentage of score needed to pass the examination is {(60X + 35)/100X × 100}
⇒ (245 × 100)/350 = 70
∴ Meena need to score 70% to pass the examination.
Q3: In a class, 60% of the students are girls and the rest are boys. There are 30 more girls than boys. If 68% of the students, including 30 boys, pass an examination, the percentage of the girls who do not pass is [TITA 2019]
Ans: 20
Sol:
Q4: In 2010, a library contained a total of 11500 books in two categories - fiction and non-fiction. In 2015, the library contained a total of 12760 books in these two categories. During this period, there was 10% increase in the fiction category while there was 12% increase in the non-fiction category. How many fiction books were in the library in 2015? [2019]
(a) 6600
(b) 6160
(c) 6000
(d) 5500
Ans: a
Increase in books = 12760 - 11500 = 1260+
x (11500 - x) = 1260
10x + 12 x 11500 - 12x = 126000
x = 6000 books
So, Fiction books in 2015, 6000 + 600 = 6600 books
Q5: In an examination, the score of A was 10% less than that of B, the score of B was 25% more than that of C, and the score of C was 20% less than that of D. If A scored 72, then the score of D was [TITA 2019]
Ans: 80
Sol:
From the data,
A scored 72
A's score was 10% less than B
So, Score of B = 80
We know that B was 25% more than C
So, C x (5/4) = 80
C = 64
Now, we know that D scored 20% less than D
So, C = (4/5) x D
64 = (4/5) x D
D = 80 marks
2018
Q1: In an examination, the maximum possible score is N while the pass mark is 45% of N. A candidate obtains 36 marks, but falls short of the pass mark by 68%. Which one of the following is then correct? [2018]
(a) N ≤ 200
(b) 243 ≤ N ≤ 252
(c) N ≥ 253
(d) 201 ≤ N ≤ 242
Ans: b
Sol:
Given Max. mark = N and Pass mark = 45% of N
A scores 36 marks and falls short of the pass mark by 68%
This means the pass mark must be reduced by (100 - 68)% = 32%
So, A scored 32% (45% N) = 36
N = 250 marks
The only option whose range falls within the obtained value is (b) 243 ≤ N ≤ 252
2017
Q1: Arun's present age in years is 40% of Barun's. In another few years, Arun's age will be half of Barun's. By what percentage will Barun's age increase during this period? [TITA 2017]
Ans: 20
Sol:
Given that Arun's present age in years is 40% of Barun's. And after few years, Arun’s age will be half of Barun’s. We have to find by what percentage will Barun’s age increase during this period.
So Arun’s present age is 2x and Barun’s present age will be equal to 5x.
2(2x + y) = 5x + y
4x + 2y = 5x + y
y = x
So 2x and 5x becomes 3x and 6x respectively.
By what percentage will Barun's age increase during this period is that x increases of 5x so it increases by 20%.
Hence 20% of Barun’s age will increase during this period.
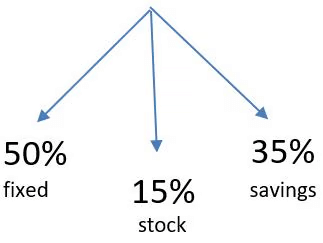
Q2: Ravi invests 50% of his monthly savings in fixed deposits. Thirty percent of the rest of his savings is invested in stocks and the rest goes into Ravi's savings bank account. If the total amount deposited by him in the bank (for savings account and fixed deposits) is Rs 59500, then Ravi's total monthly savings (in Rs) is: [TITA 2017]
Ans: 70000
Sol:
Ravi invests 50% of his monthly savings in fixed deposits i.e from the remaining 50%, 30% percent of the rest of his savings = 15% is invested in stocks.
And the rest i.e 50 – 15 = 35% goes into Ravi's savings bank account.
If the total amount deposited by him in the bank (for savings account and fixed deposits) is Rs 59500
i.e. 50 + 35 = 85 % ⇒ 85% of total savings = 59500
We have to find the Ravi's total monthly savings (in Rs)
⇒ Total savings =
Ravi's total monthly savings is 70000 Rupees.
Q3: The number of girls appearing for an admission test is twice the number of boys. If 30% of the girls and 45% of the boys get admission, the percentage of candidates who do not get admission is: [2017]
(a) 35
(b) 50
(c) 60
(d) 65
Ans: d
Sol:Given that the number of girls appearing for an admission test is twice the number of boys.Let x be the number of boys and 2x be the number of girls.
We have to find the % of candidates who do not get admission if 30% of the girls and 45% of the boys get admission.
Those who got admission is 1.05x and those who do not get admission is 1.95x.
So,
The percentage of candidates who do not get admission is 65%.
Q4: Out of the shirts produced in a factory, 15% are defective, while 20% of the rest are sold in the domestic market. If the remaining 8840 shirts are left for export, then the number of shirts produced in the factory is [2017]
(a) 13600
(b) 13000
(c) 13400
(d) 14000
Ans: b
Sol:
Given that in a shirt factory, 15% of the shirts produced are defective so 85% are non defective.
From this remaining 85% non defective shirts, 20% are sold in domestic market and the remaining 80% are left for export which is equal to 8840 shirts i.e. 80% of 85% of x = 8840⇒ x = 13000
The number of shirts produced in the factory is 13000
Q5: In a village, the production of food grains increased by 40% and the per capita production of food grains increased by 27% during a certain period. The percentage by which the population of the village increased during the same period is nearest to [2017]
(a) 16
(b) 13
(c) 10
(d) 7
Ans: c
Sol:
Given that the production of food grains increased by 40%.
Let initial production be y and after increase it becomes 1.4x
Per capita production of food grains increased by 27%.
Per capita income =
⇒ let the initial Per capita income be (x/y).
After increase it becomes 1.27[x/y].Hence there is an increase of 10% in the population of the village.
|
167 videos|238 docs|95 tests
|
FAQs on Percentages CAT Previous Year Questions with Answer PDF
| 1. What are percentages and how are they used in CAT exams? |  |
| 2. How can I improve my skills in solving percentage problems for the CAT? |  |
| 3. What are some common types of percentage questions asked in the CAT? |  |
| 4. How do I calculate the percentage increase or decrease? |  |
| 5. Are there any shortcuts for solving percentage problems quickly in the CAT? |  |