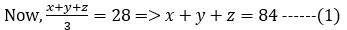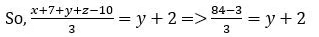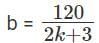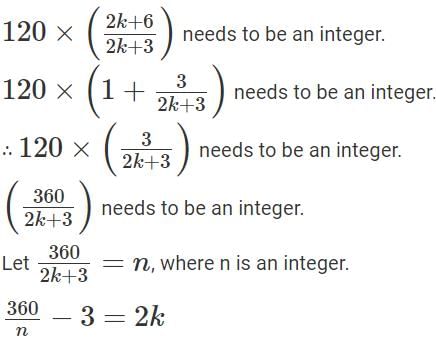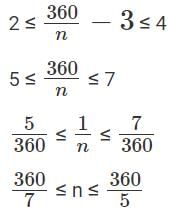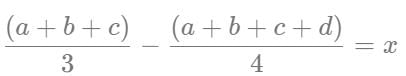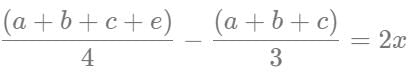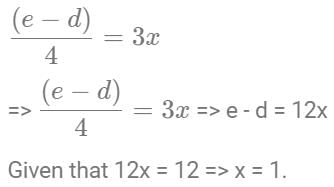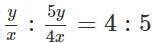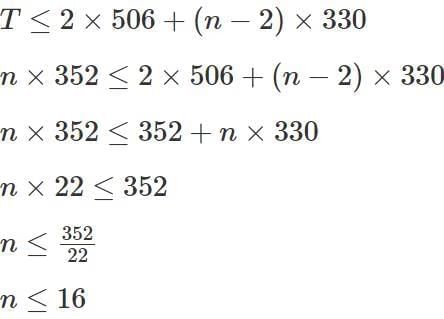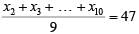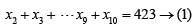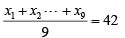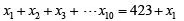Mixtures and Averages CAT Previous Year Questions with Answer PDF
From 2017 to 2024, 22 average-related questions appeared in CAT Quant, typically 2–4 questions per year. They covered topics like average calculations, number of entities, weight distributions, and score averages with conditions. Most were moderately difficult, focusing on multi-step computations involving total sums, ratio adjustments, and optimisation techniques.
2024
Q1: There are four numbers such that average of first two numbers is 1 more than the first number, average of first three numbers is 2 more than average of first two numbers, and average of first four numbers is 3 more than average of first three numbers. Then, the difference between the largest and the smallest numbers, is
Ans: 15
Sol: Let the four numbers be
a, a+2, a+7, and a+15
Clearly, the above four numbers satisfy all the conditions given in the question.
So, the required difference
= (a+15) - (a)
= 15
Q2: A company has 40 employees whose names are listed in a certain order. In the year 2022, the average bonus of the first 30 employees was Rs. 40000, of the last 30 employees was Rs. 60000, and of the first 10 and last 10 employees together was Rs. 50000. Next year, the average bonus of the first 10 employees increased by 100%, of the last 10 employees increased by 200% and of the remaining employees was unchanged. Then, the average bonus, in rupees, of all the 40 employees together in the year 2023 was
(a) 95000
(b) 85000
(c) 80000
(d) 90000
Ans: (a)
Sol: Let the average bonuses for the first 10, next 10, the next 10 and the last 10 employees be x, y, z and w respectively.
Now, A.T.Q,Adding the first two,
we get x + 2 (y + z) + w = 300,000
Now, putting the value of (x + w), we get
y + z = 100000
Using the above, we get
x = 20000 and w = 80000
When the average of the first 10 employees increases by 100%, then, it changes from 20,000 to 40,000
The average of the last 10 increases by 200%; then, it changes from 80,000 to 240,000
The total of all the four would be 40,000 + 100,000 + 240,000 = 380,000
Giving the average 380,000 / 4 = 95,000
Hence, option A is the required answer.
Q3: The average of three distinct real numbers is 28. If the smallest number is increased by 7 and the largest number is reduced by 10, the order of the numbers remains unchanged, and the new arithmetic mean becomes 2 more than the middle number, while the difference between the largest and the smallest numbers becomes 64. Then, the largest number in the original set of three numbers is
Ans: 70
Sol: Let the numbers be x, y, and z where x < y < z.
Now, the smallest number is increased by 7, the largest number is reduced by 10, and the new arithmetic mean is 2 more than the middle number.
y = 25Also, we have
(z – 10) – (x + 7) = 64 => z – x = 81 …(2)
Putting the value of y in (1), we get
z + x = 59 …(3)
Adding (2) and (3) we get
z = 70
Hence, 70 is the required answer.
2023
Q1: In an examination, the average marks of 4 girls and 6 boys is 24. Each of the girls has the same marks while each of the boys has the same marks. If the marks of any girl is at most double the marks of any boy, but not less than the marks of any boy, then the number of possible distinct integer values of the total marks of 2 girls and 6 boys is [2023]
(a) 19
(b) 21
(c) 20
(d) 22
Ans: b
Sol:
Let the marks of each girl in the class be g and the marks of each boy be b.
Since, the average marks of 4 girls and 6 boys is 24…
4g + 6b = 24 × 10 = 240
A girl scores more than or equal to the score of a boy but never more than double the score.
Therefore, g = kb, where 1 ≤ k ≤ 2
4(kb) + 6b = 240
b(4k + 6) = 240
b(2k + 3) = 120
Finally we need 2g + 6b = b(2k + 6) to be an integer.
Since, 1 ≤ k ≤ 2
2 ≤ 2k ≤ 4
51.42 ≤ n ≤ 72
52 ≤ n ≤ 72
Therefore, n can take 21 values, 52 to 72 both inclusive.
For all these values k takes a distinct value from 1 to 2 and 2g + 6b takes a distinct integral value.
Choice B is the correct answer.
Q2: There are three persons A, B and C in a room. If a person D joins the room, the average weight of the persons in the room reduces by x kg. Instead of D, if person E joins the room, the average weight of the persons in the room increases by 2x kg. If the weight of E is 12 kg more than that of D, then the value of x is [2023]
(a) 2
(b) 0.5
(c) 1
(d) 1.5
Ans: c
Sol:
Let us assume that A, B, C, D, and E weights are a, b, c, d, and e.
1st condition
2nd condition
Adding both the equations, we get:
Q3: In a company, 20% of the employees work in the manufacturing department. If the total salary obtained by all the manufacturing employees is one-sixth of the total salary obtained by all the employees in the company, then the ratio of the average salary obtained by the manufacturing employees to the average salary obtained by the non-manufacturing employees is
(a) 4 : 5
(b) 5 : 6
(c) 5 : 4
(d) 6 : 5
Ans: a
Sol: ” In a company, 20% of the employees work in the manufacturing department.”
Ratio of number of manufacturing to non-manufacturing employees = 1 : 4
So, let the number of manufacturing to non-manufacturing employees be x and 4x respectively.
“the total salary obtained by all the manufacturing employees is one-sixth of the total salary obtained by all the employees in the company,”
Ratio of total salaries of manufacturing to non-manufacturing employees = 1 : 5
So, let the total salaries of manufacturing to non-manufacturing employees be y and 5y respectively.
So, the ratio of average salaries of manufacturing to non-manufacturing employees will be
Q4: If a certain amount of money is divided equally among n persons, each one receives Rs 352. However, if two persons receive Rs 506 each and the remaining amount is divided equally among the other persons, each of them receive less than or equal to Rs 330. Then, the maximum possible value of n is
Ans: 16
Sol: Let the total amount be equal to T.
T = n × 352
“However, if two persons receive Rs 506 each and the remaining amount is divided equally among the other persons, each of them receive less than or equal to Rs 330”So, the maximum value that n can take is 16.
2022
Q1: The average of a non-decreasing sequence of N numbers a1, a2,..., an is 300. If a1, is replaced by 6a1, the new average becomes 400. Then, the number of possible values of a1, is [2022]
Ans: 14
Sol:
a1 + a2 +.....+ aN = 300N
6a1 + a2 + .....+ aN = 400N
5a1 = 100N
a1 = 20N
As the given sequence of numbers is non-decreasing sequence, N can take values from 2 to 15.
N is not equal to 1, if N = 1, then average of N numbers is 300 wouldn't satisfy.
Therefore, N can take values from 2 to 15, i.e. 14 values.
Q2: Consider six distinct natural numbers such that the average of the two smallest numbers is 14, and the average of the two largest numbers is 28. Then, the maximum possible value of the average of these six numbers is [2022]
(a) 22.5
(b) 23.5
(c) 24
(d) 23
Ans: a
Sol:
We know the sum of the first pair of numbers is 14 * 2 = 28
Sum of the last pair of numbers is 28 * 2 = 56
To maximize the average of all the 6 numbers, we must try to maximize the two numbers in between. This is possible when the last pair of numbers are 27 and 29.
The maximum average case is
a, b, 25, 26, 27, 29
Where a + b = 28
The average of these 6 numbers is 22.5
Q3: The average of three integers is 13. When a natural number n is included, the average of these four integers remains an odd integer. The minimum possible value of n is
(a) 3
(b) 1
(c) 4
(d) 5
Ans: d
Sol: It is given that average of three numbers is 13.Sum = 3*13 = 39
Q4: The average weight of students in a class increases by 600 gm when some new students join the class. If the average weight of the new students is 3 kg more than the average weight of the original students, then the ratio of the number of original students to the number of new students is
(a) 1 : 2
(b) 4 : 1
(c) 1 : 4
(d) 3 : 1
Ans: b
Sol: Let the original number of students be 'n' whose average weight is 'x'
Let the number of students added be 'm' and the average weight will be x + 3
We need to find the value of n : m
It is given, average weight of students in a class increased by 0.6 after new students are added.Therefore,
Q5: Five students, including Amit, appear for an examination in which possible marks are integers between 0 and 50, both inclusive. The average marks for all the students is 38 and exactly three students got more than 32. If no two students got the same marks and Amit got the least marks among the five students, then the difference between the highest and lowest possible marks of Amit is
(a) 20
(b) 22
(c) 21
(d) 24
Ans: a
Sol: The average marks for all the students is 38.
Sum = 5*38 = 190
To find the minimum marks scored by Amit, we need to maximise the score of remaining students.
Maximum scores sum of remaining students = 50 + 49 + 48 + 32 = 179
Minimum possible score of Amit = 190 - 179 = 11
It is given, Amit scored least. This implies maximum possible score of Amit is 31.
Difference = 31 - 11 = 20
Hence Option A is correct.
Q6: If a and b are non-negative real numbers such that a + 2b = 6, then the average of the maximum and minimum possible values of (a + b) is
(a) 3.5
(b) 4.5
(c) 4
(d) 3
Ans: b
Sol:
a + 2b = 6 (a and b are non-negative real numbers)
Minimum value that a and b can take is 0.
If a = 0, b = 3 => a+ b = 3
If a = 1, b = 2.5 => a + b = 3.5
If b = 0, a = 6 => a + b = 6
So, the average of max and min value of (a + b) = (3+6)/2 = 4.5
Q7: The average of all 3-digit terms in the arithmetic progression 38, 55, 72, ..., is
Ans: 548
Sol:
The AP is 38, 55, 72…
Common difference = 17
First 3-digit number = 106
106 + 17k < 1000
k = 52
i.e., average of 53 terms starting from 106 having CD = 17
½(2*106 + 52*17) = 548
Q8: In an examination, the average marks of students in sections A and B are 32 and 60, respectively. The number of students in section A is 10 less than that in section B. If the average marks of all the students across both the sections combined is an integer, then the difference between the maximum and minimum possible number of students in section A is
Ans: 63
Sol:
Let there be x students in Sec A and x + 10 students in Sec B
Average = [32x + 60(x+10)]/(2x+10) = 46 + 70/(x+5)
Max x = 65 => Average = 47
Min x = 2 => Average = 56
So, 65 – 2 = 63
2021
Q1: In a football tournament, a player has played a certain number of matches and 10 more matches are to be played. If he scores a total of one goal over the next 10 matches, his overall average will be 0.15 goals per match. On the other hand, if he scores a total of two goals over the next 10 matches, his overall average will be 0.2 goals per match. The number of matches he has played is
Ans: 10
Sol: Let Total matches played be n and in initial n-10 matches his goals be x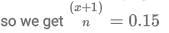
we get x+1 =0.15n (1)
From condition (2) we get :we get x+2 = 0.2n (2)
Subtracting (1) and (2)
we get 1 =0.05n
n =20
So initially he played n-10 =10 matches
Q2: Suppose hospital A admitted 21 less Covid infected patients than hospital B, and all eventually recovered. The sum of recovery days for patients in hospitals A and B were 200 and 152, respectively. If the average recovery days for patients admitted in hospital A was 3 more than the average in hospital B then the number admitted in hospital A was [2021]
Ans: 35
Sol:
Let the number of Covid patients in Hospitals A and B be x and x+21 respectively. Then, it has been given that:
16x + 1400 = x(x + 21)
x2 + 5x − 1400 = 0
(x + 40)(x - 35) = 0
Hence, x = 35.
Q3: Onion is sold for 5 consecutive months at the rate of Rs 10, 20, 25, 25, and 50 per kg, respectively. A family spends a fixed amount of money on onion for each of the first three months, and then spends half that amount on onion for each of the next two months. The average expense for onion, in rupees per kg, for the family over these 5 months is closest to
(a) 26
(b) 18
(c) 16
(d) 20
Ans: b
Sol: Let us assume the family spends Rs. 100 each month for the first 3 months and then spends Rs. 50 in each of the next two months.
Then amount of onions bought = 10, 5, 4, 2, 1, for months 1-5 respectively.
Total amount bought = 22kg.
Total amount spent = 100+100+100+50+50 = 400.
Average expense = 400/22 = Rs. 18.18 ≈ 18
2020
Q1: In a group of 10 students, the mean of the lowest 9 scores is 42 while the mean of the highest 9 scores is 47. For the entire group of 10 students, the maximum possible mean exceeds the minimum possible mean by [2020]
(a) 4
(b) 3
(c) 5
(d) 6
Ans: aSol:
(1) - (2) = x10 - x1 = 45
Let x1 be the least number
x10 be the largest number
Given
Sum of 10 observationsSince the minimum value of x10 is 47, the minimum value of x1 is 2, minimum average
=The maximum value of x1 is 42,
Maximum average =Required difference = 4
2019
Q1: Ramesh and Gautam are among 22 students who write an examination. Ramesh scores 82.5. The average score of the 21 students other than Gautam is 62. The average score of all the 22 students is one more than the average score of the 21 students other than Ramesh. The score of Gautam is [2019]
(a) 51
(b) 53
(c) 49
(d) 48
Ans: a
Sol:
It is given that, a1, a2, a3,..... Ramesh, Gautham, ...., a22 writes an examination
Given that, Average score of the 21 students other than Gautham = 62
So, Total Score - Gautham's score = 62 x 21
Ramesh scored 82.5
It is given that, when Ramesh leaves, the average score drops down by 1 mark.
Which means that Ramesh scored more than the Overall class average.
Since his departure has resulted in the decrease of the overall class average by 1, his score is 21 more than the average.
Overall Class average = 82.5 - 21 = 61.5 marks
Total Score - Gautham's score = 62 x 21
Gautham's score = 61.5 x 22 - 62 x 21
Gautham's score = 1353 - 1302
Gautham's score = 51 marks
Q2: The average of 30 integers is 5. Among these 30 integers, there are exactly 20 which do not exceed 5. What is the highest possible value of the average of these 20 integers? [2019]
(a) 4
(b) 5
(c) 4.5
(d) 3.5
Ans: c
Sol:
We are told that exactly 20 of the 30 integers do not exceed 5.
That means exactly 10 of the 30 integers do exceed 5.
In order to keep the average of the 20 integers as high as possible, we need to keep the average of the 10 integers above 5 as low as possible.
Since we are dealing with integers, the least value that the 10 integers above 5 can take is 6.
So, the sum of the 10 integers = 10 * 6 = 60
So the sum of the remaining 20 integers = Total sum - 60 = 5 * 30 - 60 = 90
Hence the average of the remaining 20 is 90/20 = 4.5
Q3: In an apartment complex, the number of people aged 51 years and above is 30 and there are at most 39 people whose ages are below 51 years. The average age of all the people in the apartment complex is 38 years. What is the largest possible average age, in years, of the people whose ages are below 51 years? [2019]
(a) 25
(b) 26
(c) 27
(d) 28
Ans: d
Sol:
Let number of people aged below 51 years be n.Total number of people in a complex = 30 + n
Total age of people in a complex = (30 + n) × 38
Largest possible average age of people above 51 years is 51.
Total age of people above 51 years = 51 × 30
Total age of people below 51 years = (30 + n) × 38 - 51 × 30 = 38n - 390
Average age people below 51 years = (38n - 390)/n
Then,
For largest possible age, n = 39
∴ Required age = (38 - 390/39) = 28 years
2018
Q1: A CAT aspirant appears for a certain number of tests. His average score increases by 1 if the first 10 tests are not considered, and decreases by 1 if the last 10 tests are not considered. If his average scores for the first 10 and the last 10 tests are 20 and 30, respectively, then the total number of tests taken by him is [2018 TITA]
Ans: 60
Sol:
Let there be 'n' tests and the Overall Average score be k
Average (n) = k => Total marks = nk
So, when we ignore the first 10 questions,
Average (n-10) = k+1
Similarly, if we ignore the last 10 questions,
Average (first (n - 10)) = k - 1
It is given that when the first 10 tests are not considered, the overall average increases by 1 (Each question carries 20 marks)
Total marks – 20 × 10 = (k + 1) (n - 10)
kn – 200 = (k + 1) (n - 10) ---(1)
Similarly, If the last 10 tests are not considered, the overall average decreases by 1 (Each question carries 30 marks)
kn - 300 = (k - 1) (n - 10) ---(2)
Solving (1) and (2), we get
kn - 200 = (k + 1) (n - 10)
(-) kn - 300 = (k - 1) (n - 10)
-------------------------------------
100 = 2(n - 10)
50 = n - 10
n = 60 questions
2017
Q1: An elevator has a weight limit of 630 kg. It is carrying a group of people of whom the heaviest weighs 57 kg and the lightest weighs 53 kg. What is the maximum possible number of people in the group? [2017 TITA]
Ans: 11
Sol:
Given that an elevator has a weight limit of 630 kg.
It is carrying a group of people of whom the heaviest weighs 57 kg and the lightest weighs 53 kg.
We have to find the maximum possible number of people in the group.
We can take one person to be 57 kg and since they have asked for the maximum possible number of people it can accommodate in the lift we can take more no. of people with lightest weight.
So, at least one guy with 57 kg.
⟹ 630 – 57 = 573
⟹ 573 / 53 = 10.8 or at most there can 10 people.
Hence, 10 + 1 = 11 people
The maximum possible number of people in the group is 11.
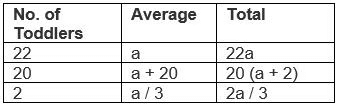
Q2: The average height of 22 toddlers increases by 2 inches when two of them leave this group. If the average height of these two toddlers is one-third the average height of the original 22, then the average height, in inches, of the remaining 20 toddlers is [2017]
(a) 30
(b) 28
(c) 32
(d) 26
Ans: c
From the given data let us assume the average height of 22 toddlers to be aIf two of them leaves this group then average height of 20 toddlers increases by 2 so a + 2
Sol:
If the average height of two toddlers who leaves the group is one third the average height of the original 22
No.of toddlers × average = Total
Hence we can write the equation in such a way that,
22a = 20(a + 2) + 2a / 3
2a – 2a / 3 = 40
⟹ 4a / 3 = 40
a = 30
We need to find the average of remaining 20 toddlers.
⟹ a + 2 = 30 + 2 = 32
|
174 videos|243 docs|95 tests
|
FAQs on Mixtures and Averages CAT Previous Year Questions with Answer PDF
| 1. What is the formula to calculate the average of a set of numbers? |  |
| 2. How can averages be used to compare different data sets? |  |
| 3. Can the average of a set of numbers change if a new number is added to the set? |  |
| 4. How are weighted averages calculated and when are they used? |  |
| 5. In what scenarios would the median be a more appropriate measure of central tendency than the average? |  |