Practice Questions: Averages | CSAT Preparation - UPSC PDF Download
The arithmetic mean—often simply called the “average” is defined as the sum of n different data divided by n. The average of a group is mainly defined as the ratio of the sum of all the items. In the group to the number of items in the group.This document will explore the calculation methods, and practical applications of the arithmetic mean across diverse fields.

Easy Level
These questions are targeted to improve your knowledge of basic concepts, though easy questions are rare in the exam. They are extremely important for conceptual understanding at the foundation level.Example 1: The average of the first ten whole numbers is
(a) 4.5
(b) 5
(c) 5.5
(d) 4
Ans: (a)
Sol: Required average = (0 + 1 + 2 + … + 9)/10 = 45/10 = 4.5
Example 2: The average of the first ten prime numbers is
(a) 15.5
(b) 12.5
(c) 10
(d) 12.9
Ans: (d)
Sol: Required average = (2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29)/10
= 129/10 = 12.9
Example 3: There are three fractions A, B, and C. If A = 1/5 and B = 1/8, the average of A, B, and C is 1/10. What is the value of C?
(a) –1/20
(b) – 1/60
(c) –1/30
(d) – 1/40
Ans: (d)
Sol: (1/5 + 1/8 + C)/3 = 1/10 => (1/5 + 1/8 + C) = 3*( 1/10)
C= 3/10 - 1/5 - 1/8
C= (12 - 8 - 5)/40
C = –1/40.
Example 4: The average age of 10 men is increased by 3 years when one of them, whose age is 54 years is replaced by a woman. What is the age of the woman?
(a) 68 years
(b) 82 years
(c) 72 years
(d) 84 years
Ans: (d)
Sol:
For a 3-year increase in the average age of 10 men,
The woman’s age would be 10 * 3 = 30 years more than the age of the man she replaces.Age of the woman = 54 + 3* 10 = 84 years.
Example 5: The average height of 13 people reduces by 2 cm if a person of height 184 cm is replaced by a new person. Find the height of the new person.
(a) 154 cm
(b) 159 cm
(c) 197 cm
(d) 158 cm
Ans: (d)
Sol:
Let the average height of the 13 people initially be A cm.
Total height of 13 people initially = 13 × A cm.
A person with height 184 cm is replaced, and the new average height becomes A − 2 cm.
Step 1: Calculate the New Total Height
New total height = 13 × (A − 2) = 13A − 26 cm.
Step 2: Find the Height of the New Person
The new total height is equal to the original total height minus the replaced person’s height plus the new person’s height:
13A − 184 + New Person’s Height = 13A − 26.
Step 3: Solve for the Height of the New Person
New Person’s Height = 184 − 26 = 158 cm.
Thus, the height of the new person is 158 cm.
Example 6: The monthly salaries of two persons A and B are in the ratio of 3: 5 respectively. If both of them received an increment of Rs. 250, then the ratio becomes 2 : 3. What were their respective salaries before the increment?
(a) Rs. 850 & Rs. 1,275
(b) Rs. 700 & Rs. 1,050
(c) Rs.750 & Rs. 1,250
(d) Rs. 650 & Rs. 975
Ans: (c)
Sol:
Let the original monthly salaries of A and B be 3x and 5x respectively.
After an increment of ₹250, their new salaries become:
- A's new salary = 3x + 250
- B's new salary = 5x + 250
According to the problem, the new ratio becomes:
3x + 2505x + 250 = 23
Step 1: Cross multiply
3(3x + 250) = 2(5x + 250)9x + 750 = 10x + 500
9x - 10x = 500 - 750
-x = -250 ⟶ x = 250
- A's original salary = 3 × 250 = ₹750
- B's original salary = 5 × 250 = ₹1250
Medium Level
Almost 70% of questions in exam are Medium-level questions. Though conceptually they seem easier, the trick is to solve the calculations faster & we curated problems for you to help you do problems more easily.
Example 1: With an average speed of 25 km/h, a train reaches its destination in time. If it goes with an average speed of 20 km/h, it is late by 1 hour. The length of the total journey is:
(a) 90 km
(b) 100 km
(c) 120 km
(d) 80 km
Ans: (b)
Sol:
Let the total length of the journey be D kilometers, and the time taken by the train at 25 km/h (on time) be T hours.
Using the formula Distance = Speed × Time, we can write:
D = 25 × T (when the train is on time)
If the train travels at 20 km/h, it is late by 1 hour. So, the new time taken is T + 1 hours, giving:
D = 20 × (T + 1)
Since both equations represent the same total distance D, we equate them:
25T = 20(T + 1)
Expand the equation:
25T = 20T + 20
5T = 20 ⟶ T = 4 hours
Now that we know T = 4 hours, substitute it into the equation D = 25 × T:
D = 25 × 4 = 100 km
Example 2: In Hotel Clarks, the rooms are numbered from 101 to 150 on the first floor, 201 to 240 on the second floor, and 316 to 355 on the third floor. In May 2018, the room occupancy was 50% on the first floor, 50% on the second floor, and 30% on the third floor. If it is also known that the room charges are ₹ 2000, ₹1000, and ₹1500 on each of the floors, then find the average income per room (in ₹) for May 2017.
(a) 676.92
(b) 880.18
(c) 783.3
(d) 650.7
Ans: (a)
Sol: The number of rooms is 50 + 40 + 40 = 130 on the three floors respectively.
Total revenues are: 25 * 2000 + 20 * 1000 + 12 * 1500 = 88000.
Hence, the required average = 88000/130 = 676.92
Example 3: The average weight of 10 men is decreased by 5 kg when one of them weighing 100 kg is replaced by another person. This new person is again replaced by another person, whose weight is 10 kg lower than the person he replaced. What is the overall change in the average due to this dual change?
(a) 5 kg
(b) 6 kg
(c) 12 kg
(d) 15 kg
Ans: (b)
Sol: The weight of the second man is 50 kg and that of the third is 40 kg.
Hence, the net result is a drop of 60 for 10 people.
Hence, 6 kg is the drop in the average.
Example 4: The average price of 3 precious diamond-studded platinum thrones is ₹ 97610498312. If their prices are in the ratio 4:7:9. The price of the cheapest is
(a) 5, 65, 66, 298.972
(b) 5, 85, 66, 29, 8987.2
(c) 58, 56, 62, 889.72
(d) None of these
Ans: (b)
Sol: The total price of the three stones would be 97610498312 * 3 = 292831494936.
Since this price is divided into three stones in the ratio of 4: 7: 9, the price of the cheapest one would be = (4 * 2928314936/20) = 58566298987.2
Example 5: The average age of a group of 15 persons is 25 years and 5 months. Two persons, each 40 years old, left the group. What will be the average age of the remaining persons in the group?
(a) 23.17 years
(b) 24.25 years
(c) 25.35 years
(d) 25 years
Ans: (a)
Sol:
25 years 5 months = 305 months, 40 years = 480 months
Therefore,
(15 * 305 – 2 * 480)/13 = 278.07 months or 23.17 years.
Example 6: There are 24 students in a class whose average marks in a subject, the maximum marks of which is 100, is 89. If 3 students leave the class, then what is the maximum by which the average could go up?
(a) 10.7
(b) 10.5
(c) 11.2
(d) 11
Ans: (d)
Sol: Sum of marks for 24 students = 24 × 89 = 2136
Average marks of a student cannot increase beyond 100.
So, total marks for 21 students cannot exceed 2100.
So, maximum increase in average = 100 – 89 = 11.
Example 7: Ajay started a firm with a capital of Rs. 28,000. After 5 months, Boman joined him and invested Rs. 40,000 in the firm. Chirag was also added as a new partner with an individual investment of Rs. 56,000 after 7 months of commencement. If at the end of the year, the profit of the firm is Rs. 32,000, what is the share of Boman?
(a) Rs. 12,000
(b) Rs. 8,000
(c) Rs. 14,000
(d) Rs. 10,000
Ans: (d)
Sol: The ratio in which profit will be shared among Ajay, Boman and Chirag = 28000 × 12 : 40000 × 7 : 560000 × 5 = 6 : 5 : 5
Hence, share of Boman = 5 / 16 × 32000 = Rs. 10,000.
Hard Level
Around 25% of these types of questions come in exam - If your target is above 95%ile, we recommend you to solve these questions as well.
Example 1: A salesman gets a bonus according to the following structure: If he sells articles worth ₹ x then he gets a bonus of ₹(x/10 – 1000). In the month of January, the value of his sales was ₹10000, in February it was ₹12000, from March to November it was ₹30000 for every month and in December it was ₹12000. Apart from this, he also receives a basic salary of ₹3000 per month from his employer. Find his average income per month (in ₹) during the year.
(a) 4533
(b) 4517
(c) 4532
(d) 4668
Ans: (a)
Sol: Replace x with the sales value to calculate the bonus in a month. Bonus = 0 in January, 200 in February 2000 each from March to November and 200 in December.
Hence, his Total bonus = 0 + 200 + 2000 x 9 + 200 = 18400.
Salary for the year = 3000 x 12. Total annual income = 36000+18400 = 54400.
Hence, the average monthly income = 4533.33.
Option (a) is closest and hence is the correct answer.
Example 2: Ramu appears in six different papers in his semester examination, where the maximum marks were 50 for each paper. His marks in these papers are in the proportion of 8 : 9 : 10 : 13 : 14 : 15. Considering his aggregate in all the papers together, he fails to obtain 50% of the total marks. What is the minimum possible additional marks Ramu should get to obtain 50% of the total marks, given that he got integral marks in each paper?
(a) 81
(b) 57
(c) 12
(d) 18
Ans: (b)
Sol: Marks obtained should be less than 50 in each paper.
There are three cases possible:
(a) Marks are 8, 9, 10, 13, 14, 15.
(b) Marks are 16, 18, 20, 26, 28, 30.
(c) Marks are 24, 27, 30, 39, 42, 45.If we take the case (a), then he required 81 marks more to get 50% of the total.
If we take the case (c), then he got more than 50% marks.
In case (b) he required 12 marks more to get 50% marks, which is less than the case (a). So this is the right answer.
|
208 videos|272 docs|138 tests
|
FAQs on Practice Questions: Averages - CSAT Preparation - UPSC
| 1. What is the formula for calculating the average? |  |
| 2. How do you find the average of a set of numbers in a bank exam question? |  |
| 3. What is the difference between mean, median, and mode? |  |
| 4. How can averages be useful in banking and finance? |  |
| 5. Are there any common mistakes to avoid when calculating averages in exams? |  |

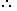 11x - (26 + 29) = 9(x -1)
11x - (26 + 29) = 9(x -1)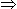 11x - 9x = 46
11x - 9x = 46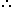 Required sale = Rs. [ (6500 x 6) - 34009 ]
Required sale = Rs. [ (6500 x 6) - 34009 ]















