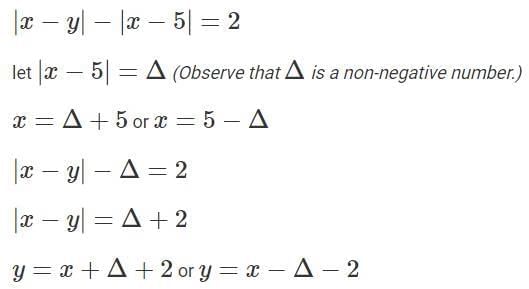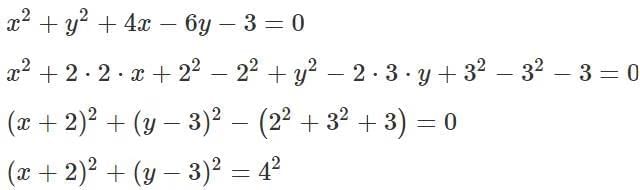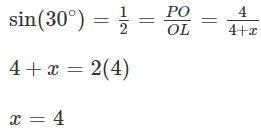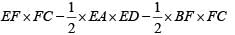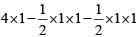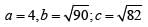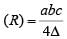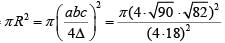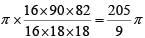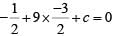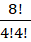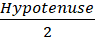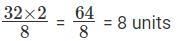Coordinate Geometry CAT Previous Year Questions with Answer PDF
2024
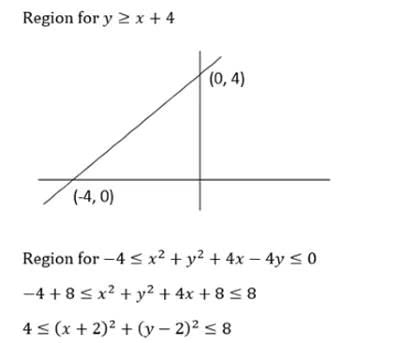
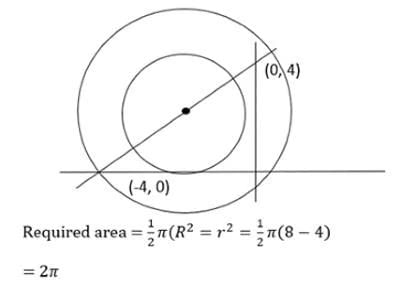
Q1: In the XY-plane, the area, in sq. units, of the region defined by the inequalities y ≥ x + 4 and -4 ≤ x2 + y2 + 4(x - y) ≤ 0 is
(a) 2π
(b) π
(c) 4π
(d) 3π
Ans: a
Sol:
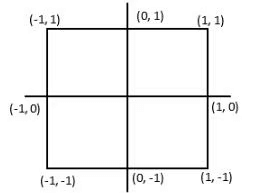
Q2: The number of distinct integer solutions (x, y) of the equation |x + y| + |x - y| = 2, is
Ans: 8
Sol: We have,
|x + y| + |x – y| = 2
Let’s analyze the situation better with graphs
Now, we can see that these are the only 8 integral points where the above equation holds.
Hence, the required answer is 8.
2023
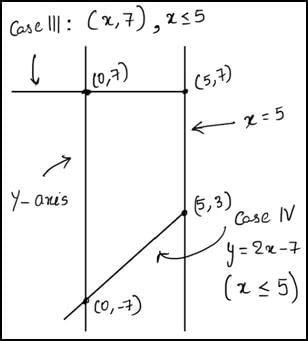
Q1: The area of the quadrilateral bounded by the Y-axis, the line x = 5, and the lines |x − y| − |x − 5| = 2, is [2023]
Ans: 45
Sol:
So, every point on the line y = 2x − 7 where x ≤ 5 satisfies the given condition.
We are to find the area enclosed by the y-axis, x = 5 and the lines of |x−y|−|x−5|=2 .
Because the area we are interested is bounded by x = 0 (y-axis) and x = 5, 0 ≤ x ≤ 5.
So, we’ll only be concerned about Case III and Case IV.
A rough sketch of the bounded region looks like…
The line y = 2x – 7 touches x = 0 and x = 5 at (0, -7) and (5, 3) respectively.
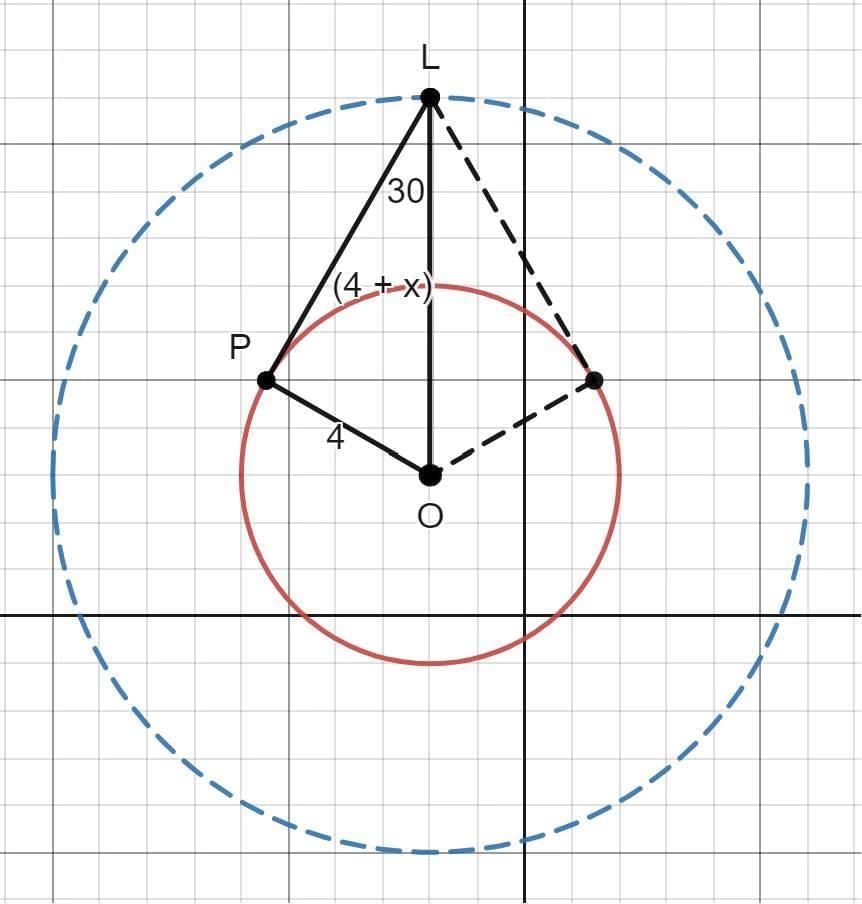
Q2: Let C be the circle x2 + y2 + 4x - 6y - 3 = 0 and L be the locus of the point of intersection of a 2 pair of tangents to C with the angle between the two tangents equal to 60°. Then, the point at which I touches the line x = 6 is
(a) (6,4)
(b) (6,8)
(c) (6,3)
(d) (6,6)
Ans: c
Sol:
This is the equation of a circle with radius 4 units and centered at (-2, 3)
From a point L we drop two tangents on the circle such that the angle between the tangents is 60o.∠LPO = 90∘
∠PLO=30∘Therefore the locus of the point L, is a circle centered at (-2, 3) and has a radius of (4 + x = 8) units.
The equation of this locus is thus, (x + 2)2 +(y − 3)2 = 82
When x = 6, we have, (8)2 +(y − 3)2 = 82 , that is y = 3
The circle , (x + 2)2 +(y − 3)2 = 82, touches the line x = 6 at (6, 3).
2022
Q1: Let ABCD be a parallelogram such that the coordinates of its three vertices A, B, C are (1, 1), (3, 4) and (−2, 8), respectively. Then, the coordinates of the vertex D are
(a) (−3, 4)
(b) (0, 11)
(c) (4, 5)
(d) (−4, 5)
Ans: d
Sol: In a parallelogram, two diagonals of parallelogram bisects each other, which concludes that mid-point of both diagonals are the same.
x = -4 and y = 5
The answer is option D.
2020
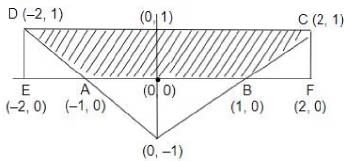
Q1: The area of the region satisfying the inequalities |x| - y ≤ 1, y ≥ 0 and y ≤ 1 is
Ans: 3
Sol:The graph of | x | - y ≤ 1, y ≥ 0 and y ≤ 1 is as follows:Area of ABCD = Area of EFCD - Area of EAD - Area of BFC
=
=
= 4 - 1 = 3 Square units.
Q2: The area, in sq. units, enclosed by the lines x = 2, y = |x - 2| + 4, the X-axis and the Y-axis is equal to [2020]
A: 8
B: 12
C: 10
D: 6
Ans: C
Sol:
The line y = |x - 2| + 4 intersects the y-axis at (0,6) and intersects x = 2 at (2, 4)
The other vertices are (0,0) and (2,0)
The figure formed is a trapezium of parallel sides 6 and 4 and the distance between the parallel sides is 2.
Required answer = (1/2) x 2 x (6 + 4) = 10
Q3: The vertices of a triangle are (0,0), (4,0) and (3,9). The area of the circle passing through these three points is [2020]
A: 14π/3
B: 12π/5
C: 123π/7
D: 205π/9
Ans: D
Sol:
Area of the triangle = 1/2 x 4 x 9 = 18
The circumradius of the triangle
Area of the circle
=
=
Q4: The points (2,1) and (-3,-4) are opposite vertices of a parallelogram. If the other two vertices lie on the line x + 9y + c = 0, then c is [2020]
A: 12
B: 14
C: 13
D: 15
Ans: B
Sol:
The given line also passes through the point of intersection of the diagonals of the parallelogram, which is the mid-point of (2,1) and (-3,-4). The mid-point of the given two points is (-1/2, -3/2).
Substituting the point in the given equation:
⇒ c = 14
2019
Q1: With rectangular axes of coordinates, the number of paths from (1,1) to (8,10) via (4,6), where each step from any point (x,y) is either to (x,y+1) or to (x+1,y) is [TITA 2019]
Ans: 3920
Sol:
Let us first consider travelling from (1,1) to (4, 6)
This means, Travelling from 1 to 4 units in the x axis → 3 horizontal movements (h h h)
And travelling from 1 to 6 units in the y axis -> 5 vertical movements (v v v v v)
No matter how we proceed, reaching from (1,1) to (4,6) requires 5 vertical movements and 3 horizontal movements.
So, Number of paths to travel from (1,1) to (4,6) = Number of ways of arranging (h h h v v v v v)
Number of ways of arranging (h h h v v v v v) =
Similarly, travelling from (4, 6) to (8, 10) requires 4 horizontal movements and 4 vertical movements
Number of ways of arranging (h h h h v v v v) =
Total number of paths =x
=
x
= 3920
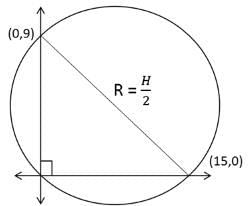
Q2: Let T be the triangle formed by the straight line 3x + 5y - 45 = 0 and the coordinate axes. Let the circumcircle of T have radius of length L, measured in the same unit as the coordinate axes. Then, the integer closest to L is [TITA 2019]
Ans: 9
Sol:
We know that the equation of the straight line is 3x + 5y = 45
The intercepts are (15,0) and (0,9) respectively
Since it's a right-angled triangle, we know that Circumradius (R) =
Circumradius ==
We know that √34 is approximately equal to 6
So, from trial and error to find the closest number, we find that the value of Circumradius is very close to 9
So, the integer closest to L = 9
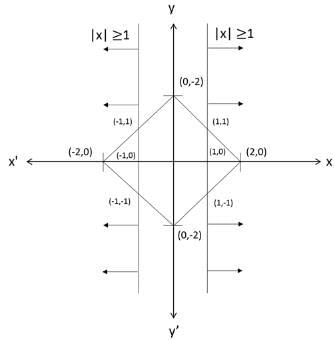
Q3: Let S be the set of all points (x,y) in the x-y plane such that |x| + |y| ≤ 2 and |x| ≥ 1. Then, the area, in square units, of the region represented by S equals [TITA 2019]
Ans: 2
Sol:
Construct the given data on a rough graph.
Required area = Sum of area of two smaller triangles [ (-2,0) (-1,1) (-1,-1) and (2,0) (1,-1) (1,1) ]
Required area = 2 x (1/2) x base x height
Required area = 1 x 2 = 2 Sq units
2018
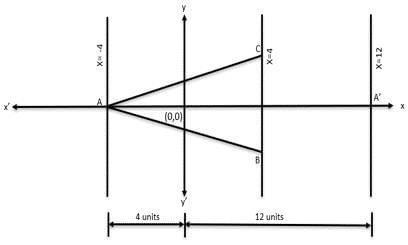
Q1: A triangle ABC has area 32 sq units and its side BC, of length 8 units, lies on the line x = 4. Then the shortest possible distance between A and the point (0,0) is [2018]
A: 4√2 units
B: 2√2 units
C: 4 units
D: 8 units
Ans: C
Sol:
Given Area (△ABC) = 32 sq units and one of the length BC = 8 units on the line x = 4
Let us draw a graph and plot the given values.
We know that area of the Triangle = 1/2 × base × height considering BC as the base, area of the Triangle = 1/2 × 8 × height = 32
Height =
Since the base lies on x = 4 and has a vertical height is of length = 8 units, A can either lie on the line x = 12 or on x = - 4
However, since we need to find the shortest possible distance between A and the origin, A should lie on the line x = - 4
So, shortest possible distance to A from the point (0,0) = 4 units
|
167 videos|238 docs|95 tests
|
FAQs on Coordinate Geometry CAT Previous Year Questions with Answer PDF
| 1. What are the basic concepts of coordinate geometry? |  |
| 2. How can we find the distance between two points using coordinate geometry? |  |
| 3. What is the equation of a straight line in coordinate geometry? |  |
| 4. How do we determine if two lines are parallel using coordinate geometry? |  |
| 5. Can coordinate geometry be used to find the midpoint of a line segment? |  |