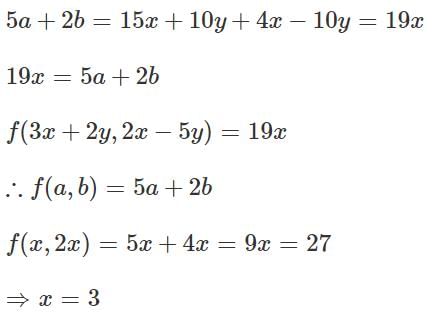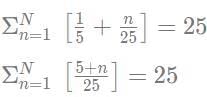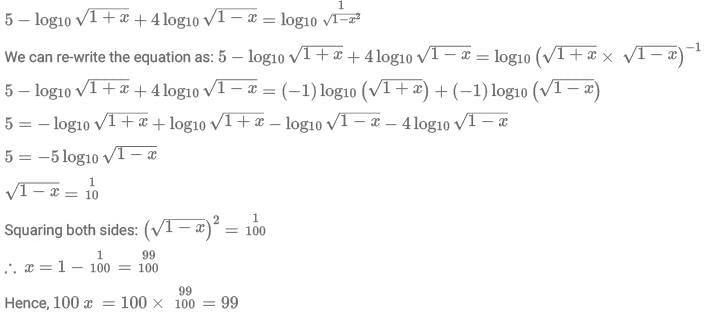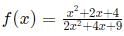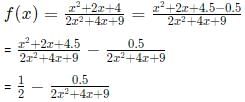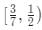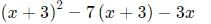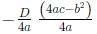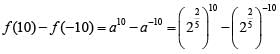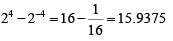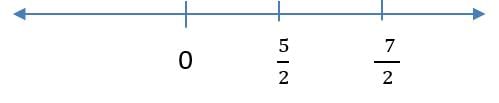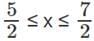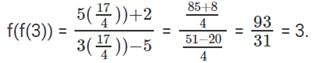CAT Previous Year Questions - Functions

Table of Contents
1. 2025
2. 2024
3. 2023
4. 2022
5. 2021
6. 2020
7. 2019
8. 2018
9. 2017
View more

From 2017 to 2025, Function-based questions consistently appeared in CAT Quant, typically 1-4 questions per year. These covered functional equations, composition of functions, domain and range, modulus and floor functions, quadratic behaviour, and multiplicative properties. Most were moderate to moderately difficult, requiring algebraic manipulation, case analysis, and careful interpretation of definitions.

2025 

Ans: a

Sol: For n = 3,4,5 and x ∈ [n, n + 1) we have [x] = n, so the equation
 
Option B and C have √10 included, which is not part of the original set. And Option D has √18. So, it is not possible.
 Option A is the answer.

Q2: Let   Then the domain of the function h(x) = f(g(x)) + g(f(x)) is all real numbers except

(a) 

(b) 

(c) 

(d) 

Ans: a

Sol: We check where  or their compositions, become undefined. First, f(x) is undefined at x = 1/2 and g(x) is undefined at x=1.
Next, for  
Since, the denominator can't be zero, x = -1 must also be excluded.
 
⇒ x = 1 is not possible, which is already excluded.
So the values at which h(x) = f(g(x)) +g(f(x)) is undefined are

Q3: If f(x) = (x² + 3x)(x² + 3x + 2) then the sum of all real roots of the equation  is
(a) -6 
(b) 6 
(c) 3 
(d) -3

Ans: d
Sol: Let (x² + 3x) be equal to k. We have, 
 

Since x is real, the discriminant of the above quadratic has to be greater than or equal to zero.

We find that 3² + 4 ∗ 9700 ≥ 0 and therefore the quadratic has real roots.

The sum of the roots will be Option D is the correct answer.

Q4: For real values of x, the range of the function  is

(a) 

(b) 

(c) 

(d) 

Ans: c

Sol: 

Equation (1) is a quadratic in x, where x is real. Therefore, the discriminant of the quadratic has to be greater than or equal to zero.

Since the coefficient of y² is positive, the quadratic will be less than zero in the range  

The quadratic will be greater than or equal to zero otherwise.

Therefore, the domain the quadratic, or possible values of y, which is the range of f(x), will be,

Option C is the correct answer.

2024

Q1: A function f maps the set of natural numbers to whole numbers, such that f(xy) = f(x)f(y) + f(x) + f(y) for all x, y and f(p) = 1 for every prime number p. Then, the value of f(160000) is 
(a) 8191
(b) 2047
(c) 4095
(d) 1023

Ans: (c)
Sol: f(16000) = f(2⁸ × 5⁴)
It is given that f(p) = 1 for any prime number p.
F(p²) = f(p) f(p) + f(p) + f(p) = 1 + 1 + 1 = 3
f(p³) = f(p²) + f(p) + f(p²) + f(p) = 3 + 3 + 1 = 7
Similarly,
f(p⁴) = 7 + 7 + 1 = 15
f(p⁵) = 15 + 15 + 1 = 31f
(p⁶) = 31 + 31 + 1 = 63
f(p⁷) = 63 + 63 + 1 = 127
f(p⁸) = 127 + 127 + 1 = 255
Now,
f(16000) = f(2⁸ × 5⁴) = f(2⁸)f(5⁴) + f(2⁸) + f(5⁴)
f(2⁸ × 5⁴) = (255 × 15) + 255 + 15 = 4095
Hence, 4095 is the required answer.

2023

Q1: Suppose f(x, y) is a real-valued function such that f(3x + 2y, 2x - 5y) = 19x , for all real numbers x and y . The value of x for which f(x, 2x) =27, is   [2023]

Ans: 3

Sol: let a = 3x + 2y; b= 2x - 5y

Let's try to write x in terms of a and b

Q2: The price of a precious stone is directly proportional to the square of its weight. Sita has a precious stone weighing 18 units. If she breaks it into four pieces with each piece having distinct integer weight, then the difference between the highest and lowest possible values of the total price of the four pieces will be 288000. Then, the price of the original precious stone is 
(a) 1296000
(b) 1944000
(c) 972000
(d) 1620000

Ans: a
Sol: The price of a precious stone is directly proportional to the square of its weight."
If W is the weight of the stone and P is the price of that stone, then P = k × W²
For the entire, unbroken stone, the price will be 18² × k = 324 k.
"If she breaks it into four pieces with each piece having distinct integer weight, then the difference between the highest and lowest possible values of the total price of the four pieces will be 288000."
The minimum profit is achieved when the weights of the broken stones are close to each other, that is, the weights are 3, 4, 5, and 6 units.
In this case the combines worth of the four stones =(3² + 4² + 5² + 6²)k = 86k
The maximum profit is achieved when the weights of the broken stones are far from each other, that is, the weights are 1, 2, 3, and 12 units.
In this case the combines worth of the four stones =(1² + 2² + 3² + 12²)k = 158k
The difference in the total value = 2,88,000.
158k - 86k = 72k = 2,88,000
k = 4,000
So, the price of the original stone = 324 k = 12,96,000

2022

Q1: Let f(x) be a quadratic polynomial in x such that f(x) ≥ 0 for all real numbers x . If f(2)=0 and f(4) = 6 , then f(-2) is equal to  [2022]
(a) 12
(b) 36
(c) 24
(d) 6

Ans: c
Sol: Let, f(x) = ax² + bx + c
Since, f(x) ≥ 0,
This means that graph of f(x) is U shaped and above the x-axis.
Since f(x) = 0 at x = 2, the graph is centered at x = 2.
This means f(2 - k) = f(2 + k).
f(2 - 2) = f(2 + 2)
f(0) = f(4)
f(0) = 6
f(0) = 6
c = 6
f(4) = 6
16 a + 4 b + 6 = 6
f(2) = 0
4 a + 2 b + 6 = 0
Solving the two equations...

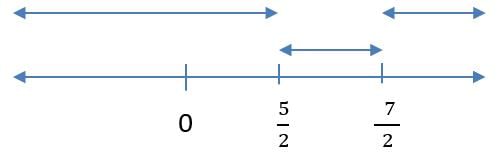
Q2: Let 0 ≤ a ≤ x ≤ 100 and f(x) = |x - a| + |x - 100| + |x - a - 50|.Then the maximum value of f(x) becomes 100 when a is equal to 
(a) 25
(b) 0
(c) 100
(d) 50

Ans: d
Sol: x>=a, so |x-a| = x-a
x<100, so |x-100| = 100-x
f(x) = (x-a) + (100-x) + |x-a-50| =100
or, |x-a-50| = a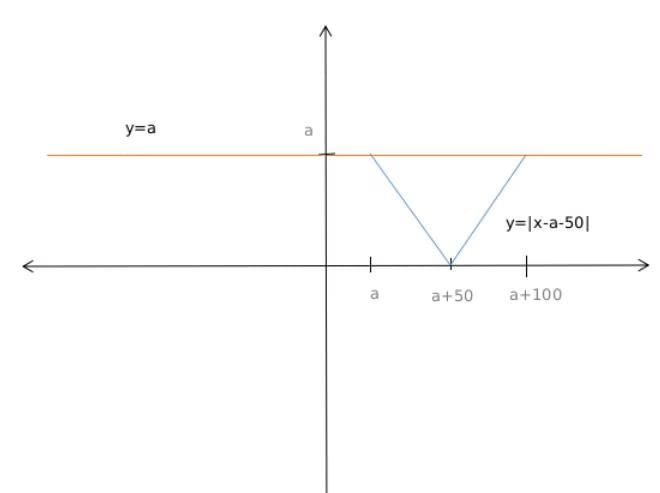
 

From the graph we can can see that when x=a then
|x-a-50|=a
or, a= 50
Similarly when x=a+100
|x-a-50|=a
or, a= 50
So value of a is 50 when f(x) is 100.

Q3: For any real number x, let [x] be the largest Integer less than or equal to x. If 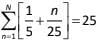 them N is 

Ans: 44
Sol: It is given,

For n = 1 to n = 19, value of function is zero.
For n = 20 to n = 44, value of function will be 1.
44 = 20 + n - 1
n = 25 which is equal to given value.
This implies N = 44

Q4: Suppose for all integers x, there are two functions f and g such that f(x) + f(x - 1) - 1 = 0) and g(x) = x². f(x² - x) = 5, then the value of the sum f(g(5)) + g(f(5)) is 

Ans: 12
Sol:
f(x) + f(x - 1) = 1; g(x) = x²
f(x² - x) = 5
f(g(5)) + g(f(5)) = ?
g(5) = 25
So, we just need to find the value of f(25) + g(f(5))
f(6) + f(5) = 1 & f(3² - 3) = f(6) = 5
=> f(5) = -4
=> g(f(5)) = 16
f(5) + f(4) = 1
=> f(4) = 5
We see a pattern for the value of f(x): 5, -4, 5,....
So, f(25) = -4
Hence, f(g(5)) + g(f(5)) = -4 + 16 = 12

Q5: Let r be a real number and  Then, the equation f(x) = f(f(x)) holds for all real values of x where 
(a) x ≠ r
(b) x > r
(c) x ≥ r
(d) x ≤ r

Ans: d
Sol:
If x = r, then f(x) = 2x - r = r
f(f(x)) = f(r) = 2r - r = r
So, f(x) = f(f(x)) for x = r
Hence, options 3 and 4 eliminated.
For x < r, f(x) = r and f(f(x)) = f(r) = r
Hence, option 1, x ≤ r is correct.

2021

Q1: If 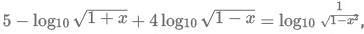 then 100x equals 

Ans: 99
Sol: 

Q2: For all real values of x, the range of the function 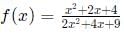 is  [2021]
(a)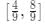 
(b)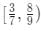 
(c)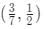 
(d)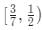 

Ans: d

Sol: 
If we closely observe the coefficients of the terms in the numerator and denominator, we see that the coefficients of the x² and x in the numerators are in ratios 1:2. This gives us a hint that we might need to adjust the numerator to decrease the number of variables.

Now, we only have terms of x in the denominator.
The maximum value of the expression is achieved when the quadratic expression 2x²
 + 4x + 9 achieves its highest value, that is infinity.
In that case, the second term becomes zero and the expression becomes 1/2. However, at infinity, there is always an open bracket ')'.
To obtain the minimum value, we need to find the minimum possible value of the quadratic expression.
The minimum value is obtained when 4x + 4 = 0 [d/dx = 0]
x = -1.
The expression comes as 7. 
The entire expression becomes 3/7.
Hence,

Q3: If f(x) = x² - 7x and g(x) = x + 3, then the minimum value of f(g(x)) - 3x is:  [2021]
(a) -20
(b) -12
(c) -15
(d) -16

Ans: d
Sol: Now we have :
f(g(x)) - 3x
so we get f(x + 3) - 3x
=
= x² - 4x - 12
Now minimum value of expression =
We get - (16 + 48)/4
= -16

2020

Q1: If f (x + y) = f (x) f (y) and f (5) = 4, then f (10) - f (-10) is equal to   [2020]
(a) 0
(b) 15.9375
(c) 3
(d) 14.0625

Ans: b

Sol: Given f ( x + y ) = f ( x) f (y)
f ( x) = a^x ( where a is a constant ) Given, f (5) = 4 ⇒ a⁵ = 4 ⇒ a = 2^{2/ 5}

=

2019

Q1: For any positive integer n, let f(n) = n(n + 1) if n is even, and f(n) = n + 3 if n is odd. If m is a positive integer such that 8f(m + 1) - f(m) = 2, then m equals  [2019 TITA]

Ans: 10

Sol: If n is even, f(n) = n (n + 1)
So, f (2) = 2(2 + 1) = 2 (3) = 6
If n is odd, f(n) = n + 3
f (1) = 1 + 3 = 4
It is given that, 8 x f(m + 1) - f(m) =2
So, m can either be even or odd
Case-1: If m were even and m + 1 odd
So, 8 x f(m + 1) - f(m) =2
8(m + 4) - m (m + 1) = 2
8m + 32 - m² - m = 2
m² - 7m - 30 = 0
(m-10) (m + 3) = 0
m = 10 or -3
m = 10, since m is positive
Case-2: If m were even and m + 1 odd
8 x f(m + 1) - f(m) =2
8 (m + 1) (m + 2) - (m + 3) = 2
Now, let us substitute m = 1 which is the minimum possible value
8 (1 + 1) (1 + 2) - (1 + 3) ≠ 3
Case 2 does not work

Q2: Consider a function f(x + y) = f(x) f(y) where x , y are positive integers, and f(1) = 2. If f (a + 1) + f (a + 2) + ..... + f(a + n) = 16 (2ⁿ - 1) then a is equal to.  [2019 TITA]

Ans: 3

Sol: We know that f(x + y) = f(x) f(y)
Let x = a and y = 1,
f (a + 1) = f(a). f (1)
f(a + 1) = f(a). 2
f(a + 2) = f(a + 1) f(1)
f(a+2) = f(a) x 2 x 2 = f(a) x 2²
Similarly, f(a + n) = f(a) x 2ⁿ
(a + 1) + f (a + 2) + ..... + f(a + n) = f(a) {2¹ + 2² + 2³ +...+2ⁿ}
(a + 1) + f (a + 2) + ..... + f(a + n) = 2f(a) {1 + 2 + 2² + 2³ +...+ 2^n-1}, which is an infinite GP series
On solving,
(a + 1) + f (a + 2) + ..... + f(a + n) = 2f(a) {2ⁿ - 1}
We know that, (a + 1) + f (a + 2) + ..... + f(a + n) = 16 (2ⁿ - 1)
So, 2f(a) {2ⁿ - 1} = 16 (2ⁿ - 1)
2 f(a) = 16
f(a) = 8
We know that, f (1) = 2 , f(2) = 4 and f(3) = 8
So, a = 3

Q3: Let f be a function such that f (mn) = f (m) f (n) for every positive integers m and n. If f (1), f (2) and f (3) are positive integers, f (1) < f (2), and f (24) = 54, then f (18) equals  [2019 TITA]

Ans: 12

Sol: It is given that f (2) > 1 and f(mn) = f(m) f(n)
So, f (2) = f (2) f (1), as m and n are positive integers.
Only possible value for f (1) = 1
f (2) > 1
Now we know, f (24) = 54
So, f (2) f (3) f (4) = 54
f (3) f (2)³ = 54
Now we know, 54 = 2 x 3³
Therefore, f (2) = 3, f (3) = 2 and f (1) = 1
Now, we need to find the value of f (18)
f (18) = f (3) x f (2) x (3)
f (18) = 2 x 3 x 2 = 12
f (18) = 12

2018

Q1: If f(x + 2) = f(x) + f(x + 1) for all positive integers x, and f(11) = 91, f(15) = 617, then f(10) equals. [2018 TITA]

Ans: 54

Sol: Given, f(x+2) = f(x) + f(x + 1) f(11) = 91, f(15) = 617
We get 91 + f(12) = f(13)
Let f(12) be equal to some value 'a'
So, 91 + a = f(13).
f(12) + f(13) = f(14)
a + 91 + a = f(14)
So, f(14) = 2a + 91 f(13) + f(14) = 617
So, 91 + a + 2a + 91 = 617
3a + 182 = 617
a = 145
Substituting the value of a and f(11), we get
f(10) + 91 = 145
f(10) = 54

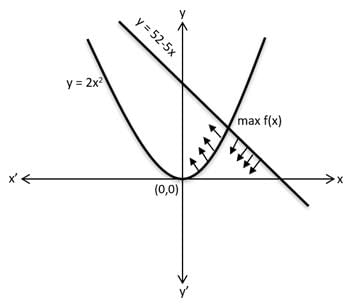
Q2: Let f(x) = min{2x², 52 - 5x}, where x is any positive real number.Then the maximum possible value of f(x) is  [2018 TITA]

Ans: 32

Sol: 

Given f(x) = min {2x², 52 - 5x}
From graph, we see that f(x) increases initially and then decreases after intersection
So, maximum value occurs when 2x² = 52 - 5x
2x² + 5x - 52 = 0
2x² - 8x + 13x - 52 = 0
2x(x - 4) + 13(x - 4) = 0
(2x + 13) (x - 4) = 0
Since x is a Positive real number, x = 4
min{2x², 52 - 5x} = min {32, 32} = 32 = max f(x)

Q3: Let f(x) = max{5x, 52 - 2x²}, where x is any positive real number.Then the minimum possible value of f(x) is  [2018 TITA]

Ans: 20

Sol: Given that f(x) = max{5x , 52 - 2x²}, where x is any positive real number.
The minimum possible value of f(x) has to found.
The minimum possible value is obtained if the two curves intersect or
5x = 52 - 2x²
2x² + 5x - 52 = 0
2x² - 8x + 13x - 52 = 0
2x(x - 4) + 13(x - 4) = 0
(2x + 13)(x - 4) = 0
x = -13 / 2 or 4
One of these would be the minimum possible value
It is given that x is a positive real number. So, we have to consider only when x = 4
When x = 4
5x = 5 × 4 = 20
52 - 2x² = 52 - 2(4)² = 20
The minimum possible value of f(x) is 20.

2017

Q1: If f₁(x) = x² + 11x + n and f₂(x) = x, then the largest positive integer n for which the equation f₁(x) = f₂(x) has two distinct real roots, is:  [2017 TITA]

Ans: 24

Sol: Given that f₁(x) = x² + 11x + n and f₂(x) = x,
Then we have to find the largest positive integer n for which the equation f₁(x) = f₂(x) has two distinct real roots.
⟹ x² + 11x + n = x
⟹ x² + 11x - x + n = 0
⟹ x² + 10n + n = 0
The discriminant should be greater than zero, D > 0.
So, b² - 4ac > 0.
⟹ 10² - 4n > 0
⟹ 100 - 4n > 0
⟹ 25 - n > 0
⟹ n = 24
Hence if f₁(x) = x² + 11x + n and f₂(x) = x, then the largest positive integer n for which the equation
f₁(x) = f₂ (x) has two distinct real roots, is 24.

Q2: Let f(x) = 2x - 5 and g(x) = 7 - 2x. Then |f(x) + g(x)| = |f(x)| + |g(x)| if and only if  [2017]

(a)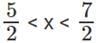 

(b)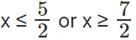 

(c)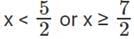 

(d) 

Ans: d

Sol: Given that f(x) = 2x - 5 and g (x) = 7 - 2x.
Consider the LHS,
|f(x) + g(x)| = |2x - 5 + 7 - 2x|
|2| = 2
So, RHS should also be 2.

On considering the RHS, |f(x)| + |g(x)|, we get
5 / 2 and 7 / 2 are the two pivotal points for which the values of f(x) and g(x) goes to zero.

We have three ranges,
1) x < 5 / 2 or
2) 5 / 2 < x < 7 / 2 or
3) x > 7 / 2.
When x lies between 0 and 5 / 2,
|f(x)| + |g(x)| = 12 - 4x
When x lies between ,
|f(x)| + |g(x)| = 2x - 5 + 7 - 2x = 2
When x is greater than 7 / 2
|f(x)| + |g(x)| = 2x - 5 + 2x - 7 = 4x - 12
Hence, out of these 3 possibilities, only  is equal to 2. So, this has to be our answer. But, is that so?
Let us consider when x = 5 / 2,
⟹ 12 - 4x = 12 - 4(5 / 2) = 2
Similarly, when x = 7 / 2,
⟹ 4x - 12 = 4(7 / 2) - 12 = 2
The value of |f(x)| + |g(x)| is equal to 2 even at x = 5 / 2 and x = 7 / 2.
Hence, the range is

Q3: If f(x) = 5x + 2 / 3x - 5 and g(x) = x² - 2x - 1, then the value of g(f(f(3))) is:  [2017]
(a) 2
(b) 1 / 3
(c) 6
(d) 2 / 3

Ans: a

Sol: Firstly, f(3) = 5(3) + 2 / 3(3)-5 = 15 + 2 / 9 - 5
⟹ f(3) = 17 / 4
Now, let us find f(f(3))

Next, we can find g(f(f(3))).
g(f(f(3))) = x² - 2x - 1
g(f(f(3))) = (x - 1)² - 2
g(f(f(3))) = (3 - 1)² - 2 = 4 - 2 = 2

Q4: Let f(x) = x² and g(x) = 2^x, for all real x. Then the value of f(f(g(x)) + g(f(x))) at x = 1 is  [2017]
(a) 16
(b) 18
(c) 36
(d) 40

Ans: c

Sol: Given that f(x) = x² and g(x) = 2^x.
We have to find the value of f(f(g(x)) + g(f(x))) at x = 1,
⟹ g(1) = 2¹ = 2 ; f(1) = 1² = 1
First, let us find the value of f(g(x)) + g(f(x)) at x = 1,
⟹ f(g(1)) + g(f(1)) = f(2) + g(1)
⟹ 2² + 2
⟹ 6
Therefore, f(g(1)) + g(f(1)) = 6.
The value of f(f(g(1)) + g(f(1))) = f(6)
⟹ f(6) = x² = 6² = 36

Q5: If f(ab) = f(a)f(b) for all positive integers a and b, then the largest possible value of f(1) is  [2017 TITA]

Ans: 1

Sol: Given that f(ab) = f(a) × f(b) for all possible integers a and b.
We have to find the largest possible value of f(1). We know that,
f(ab) = f(a) × f(b)
⟹ f(a × 1) = f(a) × f(1)
⟹ [f(a) × f(1)] - f(a) = 0
⟹ f(a)[f(1) - 1] = 0
There are two possibilities here, either f(a) = 0 or f(1) - 1 = 0.
If f(a) = 0, then it is a constant function. Hence, f(1) = 0.
But, if f(1) - 1 = 0, f(1) = 1.
Hence, f(1) = 0 or f(1) = 1.
Out of these, f(1) = 1 is the largest possible value.