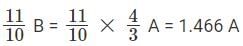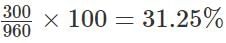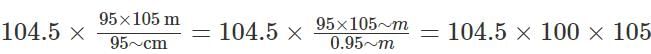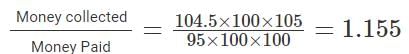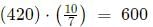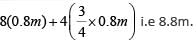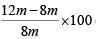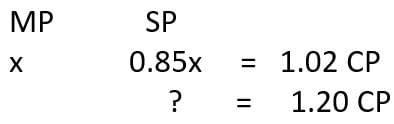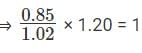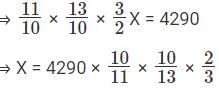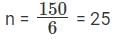Daily Practice Questions CAT Previous Year Questions with Answer PDF
2024
Q1: The selling price of a product is fixed to ensure 40% profit. If the product had cost 40% less and had been sold for 5 rupees less, then the resulting profit would have been 50%. The original selling price, in rupees, of the product is
(a) 10
(b) 14
(c) 15
(d) 20
Ans: b
Sol:
Q2: Bina incurs 19% loss when she sells a product at Rs. 4860 to Shyam, who in turn sells this product to Hari. If Bina would have sold this product to Shyam at the purchase price of Hari, she would have obtained 17% profit. Then, the profit, in rupees, made by Shyam is
Ans: 2160
Sol: Assume CP = c
So, C.P. for Bina = c
S.P. for Bina = 4860
A.T.Q,
c × 81/100 = 4860
C = 6000
If Bina has to sold to Shyam at the purchase price of Hari, then, there is a profit of 17% to Bina.
So, Cost price for Hari = 1.17 × 6000 = 7020
Hence, profit made by Shyam = 7020 – 4860 = 2160
Q3: Gopi marks a price on a product in order to make 20% profit. Ravi gets 10% discount on this marked price, and thus saves Rs 15. Then, the profit, in rupees, made by Gopi by selling the product to Ravi, is
(a) 10
(b) 20
(c) 15
(d) 25
Ans: a
Sol: Let the CP and MP of the product be C and M respectively.
M = C * 1.20
Also, SP = M * 0.90
We have, M * 0.10 = 15 ⇒ M = 150
C = 150 / 1.20 = 125, and SP = 150 * 0.90 = 135
Profit = 135 – 125 = 10
Hence, 10 is the correct answer.
Q4: The selling price of a product is fixed to ensure 40% profit. If the product had cost 40% less and had been sold for 5 rupees less, then the resulting profit would have been 50%. The original selling price, in rupees, of the product is [2024]
(a) 10
(b) 14
(c) 15
(d) 20
Ans: b
Sol: Let the original cost price be C, and the original selling price be S.
We know that S = C × 1.40.
If the cost price is reduced by 40%, the new cost price is 0.6C, and the new selling price is S−5. The new profit is 50.
S − 5 = 1.5 × 0.6C ⇒ S − 5 = 0.9C
Substituting S = 1.4C into this equation:
1.4C − 5 = 0.9C ⇒ 0.5C = 5 ⇒ C = 10
The original selling price is S = 1.4 × 10 = 14.
Q5: A shop wants to sell a certain quantity (in kg) of grains. It sells half the quantity and an additional 3 kg of these grains to the first customer. Then, it sells half of the remaining quantity and an additional 3 kg of these grains to the second customer. Finally, when the shop sells half of the remaining quantity and an additional 3 kg of these grains to the third customer, there are no grains left. The initial quantity, in kg, of grains is [2024]
(a) 50
(b) 18
(c) 36
(d) 42
Ans: d
Sol: Let us say the quantity of grains is X
For the first customer he sells X/2 + 3
Remaining is X/2 - 3
Second customer he sells: X/4 − 3/2 + 3 = X/4 + 3/2
Remaining will be X/4 - 9/2
Third customer he sells: X/8 - 9/4 + 3 = X/8 + 3/4
Remaining will be X/8 - 21/4
Now, this is said to be 0,
X/8 - 21/4 = 0
X = 42
Q6: Bina incurs 19% loss when she sells a product at Rs. 4860 to Shyam, who in turn sells this product to Hari. If Bina would have sold this product to Shyam at the purchase price of Hari, she would have obtained 17% profit. Then, the profit, in rupees, made by Shyam is [2024]
Ans: 2160
Sol: Let the cost price of the item be C
We are given that Bina sells this at 19% loss or at (1 - 0.19)C = 0.81C at 4860
This gives us the value of C at Rs. 6000
If Bina had sold this at 17% profit, the selling price would have been 1.17× 6000 = 7020
So Shyam bought the product at 4860 and sold it to Hari at 7020
Giving the profit made by Shyam to be 7020−4860 = 2160
Therefore, 2160 is the correct answer.
Q7: Gopi marks a price on a product in order to make 20% profit. Ravi gets 10% discount on this marked price, and thus saves Rs 15. Then, the profit, in rupees, made by Gopi by selling the product to Ravi, is [2024]
(a) 10
(b) 20
(c) 15
(d) 25
Ans: a
Sol: Let us say the cost price of an item is X
It is said that it is marked to make a profit of 20%.
That means it is marked at 1.2X
Ravi gets a 10% discount on the marked price,
0.9(1.2X) = 1.08X
Saves 15 rupees, so 1.2X-1.08X
0.12X=15
X=125
Profit made by Gopi is 0.08(125)=10 rupees.
2023
Q1: Gita sells two objects A and B at the same price such that she makes a profit of 20% on object A and a loss of 10% on object B. If she increases the selling price such that objects A and B are still sold at an equal price and a profit of 10% is made on object B, then the profit made on object A will be nearest to [2023]
(a) 42%
(b) 47%
(c) 45%
(d) 49%
Ans: b
Sol:
- Let A be the cost price of object A and B be the cost price of object B.
- Gita sells two objects A and B at the same price such that she makes a profit of 20% on object A and a loss of 10% on object B.
- Therefore, 1.2 × A = 0.9 × B
- 4 A = 3 B
- B = 4/3 A
- To sell object B at a profit of 10%, the selling price of B must be 1.1 B or 11/10 B
- Object A is sold at the same price as object B, that is,
- The profit obtained on object A in such a trade will be 46.66% or nearly 47%.
Q2: Minu purchases a pair of sunglasses at Rs.1000 and sells to Kanu at 20% profit. Then, Kanu sells it back to Minu at 20% loss. Finally, Minu sells the same pair of sunglasses to Tanu. If the total profit made by Minu from all her transactions is Rs.500, then the percentage of profit made by Minu when she sold the pair of sunglasses to Tanu is [2023]
(a) 35.42%
(b) 31.25%
(c) 52%
(d) 26%
Ans: b
Sol:
- “Minu purchases a pair of sunglasses at Rs.1000 and sells to Kanu at 20% profit.”
- This means, Minu purchased the glasses at Rs.1000 and sold them to Kanu at Rs.1200.
- Minu made a profit of Rs. 200 so far.
- “Then, Kanu sells it back to Minu at 20% loss.”
- This means, Kanu sold the glasses back to Minu at 80% of 1200 = Rs. 960
- “Finally, Minu sells the same pair of sunglasses to Tanu. … the total profit made by Minu from all her transactions is Rs.500”
- This means, Minu has to make a further profit of Rs. 300. She achieves this by selling the glasses back to Tanu at 960 + 300 = Rs.1260
- So the profit % in the transaction is
Q3: A merchant purchases a cloth at a rate of Rs.100 per meter and receives 5 cm length of cloth free for every 100 cm length of cloth purchased by him. He sells the same cloth at a rate of Rs.110 per meter but cheats his customers by giving 95 cm length of cloth for every 100 cm length of cloth purchased by the customers. If the merchant provides a 5% discount, the resulting profit earned by him is [2023]
(a) 4.2%
(b) 15.5%
(c) 16%
(d) 9.7%
Ans: b
Sol:
- Let's say the merchant paid for 95×100 m .
- He pays 95 × 100 × 100 rupees and gets 95 × 105 m of cloth.
- (because, he pays Rs. 100/meter and gets 5% extra cloth)
- He sells 95 cm of the cloth at Rs. 104.5 (5% discounted on Rs. 110)
- So, the total money collected by the merchant will be
- This means, the profit percentage is 15.5%
Q4: Jayant bought a certain number of white shirts at the rate of Rs 1000 per piece and a certain number of blue shirts at the rate of Rs 1125 per piece. For each shirt, he then set a fixed market price which was 25% higher than the average cost of all the shirts. He sold all the shirts at a discount of 10% and made a total profit of Rs 51000. If he bought both colors of shirts, then the maximum possible total number of shirts that he could have bought is
Ans: 407
Sol: Let the number of white and black shirts bought by Jayant be w and b respectively.
Then the total Cost Price (CP) =1000 × w + 1125 × b =1000(w + b) + 125 × b
Since the goods are marked up by 25% and then offered at a discount of 10%, the total Selling Price (SP)
= CP × 1.25 × 0.9 = 1.125 CP
This implies that there was a 12.5% of Profit, which is given to be 51, 000
12.5%(CP) = 51,000
CP = 4,08,000
1000(w + b) + 125 × b = 4,08,000
w and b are positive integers (since at least one shirt of each color needs to be purchased.)
To purchase maximum number of shirts, you need to purchase minimum number of the costlier shirts, which are the blue ones…
Observe that the total CP is a multiple of 1000. And for that to happen b should be a multiple of 8 in
1000(w + b) + 125 × b = 4,08,000.
So the minimum value of b = 8, in which case, w = 399.
Hence, the maximum number of shirts that can be purchased = 399 + 8 = 407
2022
Q1: Ankita buys 4 kg cashews, 14 kg peanuts and 6 kg almonds when the cost of 7 kg cashews is the same as that of 30 kg peanuts or 9 kg almonds. She mixes all the three nuts and marks a price for the mixture in order to make a profit of ₹1752. She sells 4 kg of the mixture at this marked price and the remaining at a 20% discount on the marked price, thus making a total profit of ₹744. Then the amount, in rupees, that she had spent in buying almonds is [2022]
(a) 1440
(b) 1176
(c) 1680
(d) 2520
Ans: c
Sol: Ankita had 4 kg cashews, 14 kg peanuts and 6 kg almonds.
In all, she had 24 kgs of nuts to sell. Let us assume the average buying price of these nuts is x rupees per kg.
Average buying price means, Whatever the per kg cost of cashews, peanuts and almonds is, when you mix 4 kg cashews, 14 kg peanuts and 6 kg almonds and get 24 kgs of nuts, let's assume each kg of nuts cost x rupees per kg.
Ankita planned to make a total profit of ₹1752 by selling these 24 kgs of nuts.
That means, she planned on making a profit of 1752/24 = ₹73 on these 24 kgs of nuts.
So the marked price of these 24 kgs of nuts is ₹‘x + 73’ per kg.
She sells 4 kg of the mixture at this marked price and the remaining at a 20% discount on the marked price, thus making a total profit of ₹744.
This means,
4(x + 73) + 0.8 * 20(x + 73) = 24 x + 744
716 = 4x
x = 179
That means the buying price of 24 kgs of these nuts is 24x = 24(179) = ₹4296
In other words, the buying price of 4 kg cashews, 14 kg peanuts and 6 kg almonds is ₹4296.
We are told that “the cost of 7 kg cashews is the same as that of 30 kg peanuts or 9 kg almonds.”
7C = 30 P = 9 A
Where C, P and A are the per kg buying costs of Cashews, Peanuts and Almonds respectively.
Let 7C = 30 P = 9 A = 630k
C = 90k
P = 21k
A = 70k
We know that, the buying price of 4 kg cashews, 14 kg peanuts and 6 kg almonds is ₹4296.
4 C + 14 P + 6 A = 4296
4 (90k) + 14 (21k) + 6 (70k) = 4296
360k + 294k + 420k = 1074k = 4296
k = 4
A = 70k = 280
The buying price of Cashews is ₹280 per kg.
The total money spent on Cashews is 6C = ₹1680
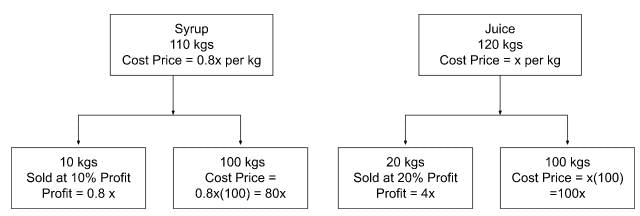
Q2: Amal buys 110 kg of syrup and 120 kg of juice, syrup being 20% less costly than juice, per kg. He sells 10 kg of syrup at 10% profit and 20 kg of juice at 20% profit. Mixing the remaining juice and syrup, Amal sells the mixture at ₹ 308.32 per kg and makes an overall profit of 64%. Then, Amal's cost price for syrup, in rupees per kg, is [2022]
Ans: 160
Sol: Let the Cost Price of Juice be rupees x per kg.
Since the Cost Price of Syrup is 20% less than the Cost Price of Juice, Cost Price of Syrup is 0.8x per kg.
Total Cost Price of Syrup = 110 * 0.8 x = 88 x
Total Coat Price of Juice = 120 * x = 120x
Total Cost Price = 88x + 120x = 208x
Since the Overall Profit Percentage is 64%.
Total Profit = 0.64(208x) = 133.12x
The profit generated on selling 10 kgs of Syrup which costs 0.8x rupees per kg at 10% Profit = 0.1 * 10 * 0.8x = 0.8x
The profit generated on selling 20 kgs of Juice which costs x rupees per kg at 20% Profit = 0.2 * 20 * x = 4x
The remaining profit (133.12x - (0.8x + 4x) = 128.32x) is generated by selling 100 kgs of Syrup and 100 kgs of Juice at ₹ 308.32 per kg.
The total Selling Price of 100 kgs of Syrup and 100 kgs of Juice is 200 * 308.32 = 2(30832)
Cost Price of 100 kgs of Syrup = 0.8x * 100 = 80x
Cost Price of 100 kgs of Juice = x * 100 = 100x
Total Cost Price = 80x + 100x = 180x
Profit = Selling Price - Cost Price
128.32x = 2(30832) - 180x
308.32x = 2(30832)
x = 200
Cost Price of Syrup per kg = 0.8 x = 0.8(200) = ₹160 per kg.
Q3: Manu earns ₹4000 per month and wants to save an average of ₹550 per month in a year. In the first nine months, his monthly expense was ₹3500, and he foresees that, tenth month onward, his monthly expense will increase to ₹3700. In order to meet his yearly savings target, his monthly earnings, in rupees, from the tenth month onward should be
(a) 4350
(b) 4400
(c) 4300
(d) 4200
Ans: b
Sol:
Earning 4000 pm
Aspired savings 550 pm, i.e., 550x12 = 6600 per year
Savings in first 9 months = 9(4000 – 3500) = 4500
To achieve the sum of 6600, the sum of savings in the remaining 3 months should be 6600 – 4500 = 2100. i.e., 700 pm
Let his per month earnings in the last 3 months be x.
=> x – 3700 = 700
=> x = 4400
2021
Q1: Amal purchases some pens at ₹ 8 each. To sell these, he hires an employee at a fixed wage. He sells 100 of these pens at ₹ 12 each. If the remaining pens are sold at ₹ 11 each, then he makes a net profit of ₹ 300, while he makes a net loss of ₹ 300 if the remaining pens are sold at ₹ 9 each. The wage of the employee, in INR, is
Ans: 1000
Sol: Let the number of pens purchased be n. Then the cost price is 8n. The total expenses incurred would be 8n+W, where W refers to the wage.
Then SP in the first case = 12 x 100 + 11 x (n-100)
Given profit is 300 in this case: 1200+11n-1100-8n-W=300 =>3n-W = 200
In second case: 1200+9n-900-8n-W=-300 (Loss). => W-n = 600.
Adding the two equations: 2n = 800
n = 400.
Thus W = 600 + 400 = 1000
Q2: A person buys tea of three different qualities at ₹ 800, ₹ 500, and ₹ 300 per kg, respectively, and the amounts bought are in the proportion 2 : 3 : 5. She mixes all the tea and sells one-sixth of the mixture at ₹ 700 per kg. The price, in INR per kg, at which she should sell the remaining tea, to make an overall profit of 50%, is [2021]
(a) 653
(b) 688
(c) 692
(d) 675
Ans: b
Sol:
- Considering the three kinds of tea are A, B, and C.
- The price of kind A = Rs 800 per kg.
- The price of kind B = Rs 500 per kg.
- The price of kind C = Rs 300 per kg.
- They were mixed in the ratio of 2 : 3: 5.
- 1/6 of the total mixture is sold for Rs 700 per kg.
- Assuming the ratio of mixture to A = 12kg, B = 18kg, C =30 kg.
- The total cost price is 800 x 12 + 500 x 18 + 300 x 30 = Rs 27600.
- Selling 1/6 which is 10kg for Rs 700/kg the revenue earned is Rs 7000.
- In order to have an overall profit of 50 percent on Rs 27600.
- The selling price of the 60 kg is Rs 27600 x 1.5 = Rs 41400.
- Hence he must sell the remaining 50 kg mixture for Rs 41400 - Rs 7000 = 34400.
- Hence the price per kg is Rs 34400/50 = Rs 688
Q3: Anil, Bobby, and Chintu jointly invest in a business and agree to share the overall profit in proportion to their investments. Anil’s share of investment is 70%. His share of profit decreases by ₹ 420 if the overall profit goes down from 18% to 15%. Chintu’s share of profit increases by ₹ 80 if the overall profit goes up from 15% to 17%. The amount, in INR, invested by Bobby is [2021]
(a) 2000
(b) 2400
(c) 2200
(d) 1800
Ans: a
Sol:
- Let the amount invested by Anil Bobby and Chintu be x, y, and z.
- Considering x + y + z = 100 x p.
- Given Anil's share was 70 percent = 70 x p.
- As per the information provided :
- His share of profit decreases by ₹ 420 if the overall profit goes down from 18% to 15%.
- Since the profits are distributed in the ratio of their investments :
- With a 3% decrease in the profits the value of profit earned by A decreased by Rs 420 which was 70 percent of the total invested.
- Hence for all three of them would be combinedly losing
- Hence 3 percent profit was equivalent to Rs 600.
- The initial investment is equivalent to Rs 20000.
- This is the total amount invested.
- Chintu's profit share increased by Rs 80 when the profit percentage increased by 2 %. A 2 percent increase in profit is equivalent to Rs 20000*2/100 = Rs 400.
- Of which Rs 80 is earned by Chintu which is 20% of the total Rs 400.
- Hence he invested 20% of the total amount.
- Bobby invested the other 10 percent.
- 10 percent of Rs 20000 = Rs 2000
Q4: One part of a hostel’s monthly expenses is fixed, and the other part is proportional to the number of its boarders. The hostel collects ₹ 1600 per month from each boarder. When the number of boarders is 50, the profit of the hostel is ₹ 200 per boarder, and when the number of boarders is 75, the profit of the hostel is ₹ 250 per boarder. When the number of boarders is 80, the total profit of the hostel, in INR, will be [2021]
(a) 20200
(b) 20500
(c) 20800
(d) 20000
Ans: b
Sol: Profit per boarder = Total profit / Number of boarders.
Let the number of boarders be n.
Profit/boarder = 1600 - (Total cost/n)
Let the total cost be a + bn, where a = fixed, and b is the variable additional cost per boarder.
Profit/boarder = 1600 - (a + bn)/n
Profit/boarder = 1600 - a/n - b
1600 - a/50 - b = 200
1600 - a/75 - b = 250
Solving, we get a = 7500, and b = 1250
Hence, total profit with 80 people = 80 ( 1600 - 7500/80 - 1250) = 80 (350 - 7500/80)
= 28000 - 7500 = Rs. 20500
2020
Q1: A person spent Rs 50000 to purchase a desktop computer and a laptop computer. He sold the desktop at 20% profit and the laptop at 10% loss. If overall he made a 2% profit then the purchase price, in rupees, of the desktop is [2020]
Ans: 20000
Sol:
- Using Alligation Rule, the ratio of cost prices of desktop and laptop will be
- i.e., 2: 3
- ∴ The cost of desktop = 2/5 x 50000 = 20,000
Q2: Anil buys 12 toys and labels each with the same selling price. He sells 8 toys initially at 20% discount on the labeled price. Then he sells the remaining 4 toys at an additional 25% discount on the discounted price. Thus, he gets a total of Rs 2112, and makes a 10% profit. With no discounts, his percentage of profit would have been [2020]
(a) 60
(b) 55
(c) 50
(d) 54
Ans: c
Sol:
- Let the cost price and marked price of each toy be c and m respectively.
- Overall selling price =
- Given, 110% of 12c = 8.8m
- ⇒ c = 2m/3
- Overall CP = 12 x 2m/3 = i.e. 8m
- Required profit percentage =
- = 50%
Q3: A man buys 35 kg of sugar and sets a marked price in order to make a 20% profit. He sells 5 kg at this price, and 15 kg at a 10% discount. Accidentally, 3 kg of sugar is wasted. He sells the remaining sugar by raising the marked price by p percent so as to make an overall profit of 15%. Then p is nearest to [2020]
(a) 31
(b) 22
(c) 35
(d) 25
Ans: d
Sol:
- Let the CP and MP of each kg of sugar be 10x and 12x respectively.
- Total cost price = 35 x 10x = 350x
- Total selling price = 35 x 10 x x1.15 = 402.5x
- Selling price already realized = 5 x 12x + 15 x 12 x x 0.9 + 3 x 0 + 12 x 12 x x (1 + p / 100) = 402.5 x
- 60 + 162 + 0 + 144(1 + p / 100) = 402.5
- p = 25.34% ≈25%
2019
Q1: On selling a pen at 5% loss and a book at 15% gain, Karim gains Rs. 7. If he sells the pen at 5% gain and the book at 10% gain, he gains Rs. 13. What is the cost price of the book in Rupees? [2019]
(a) 80
(b) 85
(c) 100
(d) 95
Ans: a
Sol:
- From the question, let us frame the following equations
- -P x 5% + b x 15% = 7 ---(1)
P x 5% + b x 10% = 13 --- (2)
________________________
(+)
b x (25%) = 20- Price of Book = b = Rs. 80
Q2: Mukesh purchased 10 bicycles in 2017, all at the same price. He sold six of these at a profit of 25% and the remaining four at a loss of 25%. If he made a total profit of Rs. 2000, then his purchase price of a bicycle, in Rupees, was [2019]
(a) 2000
(b) 6000
(c) 8000
(d) 4000
Ans: d
Sol:
- Let the cost price of one bicycle = Rs. x
- Total cost price = Rs. 10x
- He made a total profit of 25% on 6 cycles and 25% loss on 4 cycles and made a profit of Rs. 2000
- So, 2000 = 6*x/4- 4*x/4
- 2000 =
- x = Rs. 4000
Q3: A shopkeeper sells two tables, each procured at cost price p, to Amal and Asim at a profit of 20% and at a loss of 20%, respectively. Amal sells his table to Bimal at a profit of 30%, while Asim sells his table to Barun at a loss of 30%. If the amounts paid by Bimal and Barun are x and y, respectively, then (x - y) / p equals [2019]
(a) 1
(b) 1.2
(c) 0.7
(d) 0.50
Ans: a
Sol:
- The Shopkeeper procures the table at price 'p'
- He gains 20% on the transaction with Amal
- So, Amal buys the table at '1.2p'
- Amal sells athe table at 30% profit,
- So the Selling Price of Amal = 1.3 * 1.2p = 1.56p
- x = 1.56p
- The Shopkeeper looses 20% on the transaction with Asim
- So, Asim buys the table at '0.8p'
- Asim sells athe table at 30% loss,
- So the Selling Price of Asim = 0.7 * 0.8p = 0.56p
- y = 0.56p
- (x - y)/p = (1.56p - 0.56p)/p = 1.
2017
Q1: If a seller gives a discount of 15% on retail price, she still makes a profit of 2%. Which of the following ensures that she makes a profit of 20%? [2017]
(a) Give a discount of 5% on retail price
(b) Give a discount of 2% on retail price
(c) Increase the retail price by 2%
(d) Sell at retail price
Ans: d
Sol:
- Given that if a seller gives a discount of 15% on the retail price, she still makes a profit of 2%.
- Let us assume marked price to be x. So, selling price to be 0.85x on giving 15% discount on retail price she still makes a profit of 2%.
- We have to find which of the following options ensures that she makes a profit of 20% so the discount should be much lower.
- Hence by selling at retail price she makes a profit of 20%.
Q2: In a market, the price of medium quality mangoes is half that of good mangoes. A shopkeeper buys 80 kg good mangoes and 40 kg medium quality mangoes from the market and then sells all these at a common price which is 10% less than the price at which he bought the good ones. His overall profit is: [2017]
(a) 6%
(b) 8%
(c) 10%
(d) 12%
Ans: b
Sol:
- The price of medium quality mangoes is half that of good mangoes. He buys 80 kg of good mangoes and 40 kg medium quality mangoes from the market.
- Then sells all these at a common price which is 10% less than the price at which he bought the good ones.
- i.e. 40 + 80 = 120 kgs is sold at 1.8x.
- His overall profit can be found as follows,
- Cost price ⇒ 40x + 160x = 200x
- Selling price ⇒ 120 × 1.8x = 216x
- Hence there is 8% increase from cost price to selling price.
- His overall profit was 8%.
Q2: If Fatima sells 60 identical toys at a 40% discount on the printed price, then she makes 20% profit. Ten of these toys are destroyed in fire. While selling the rest, how much discount should be given on the printed price so that she can make the same amount of profit? [2017]
(a) 30%
(b) 25%
(c) 24%
(d) 28%
Ans: d
Sol:
- Given that if Fatima sells 60 identical toys at a 40% discount on the printed price, then she makes 20% profit. Ten of these toys are destroyed in fire.
- If she needs to make the same amount of profit by selling the remaining toys, she needs to sell them at,
- ⇒ 60 × 0.6x = 50 × y
- ⇒ 3.6x = 5 × y
- ⇒ y = 0.72x or she sells at 72% of the printed price.
- Therefore the discount to be given = 100 – 72 = 28%
Q3: The manufacturer of a table sells it to a wholesale dealer at a profit of 10%. The wholesale dealer sells the table to a retailer at a profit of 30%. Finally, the retailer sells it to a customer at a profit of 50%. If the customer pays Rs 4290 for the table, then its manufacturing cost (in Rs) is [2017]
(a) 1500
(b) 2000
(c) 2500
(d) 3000
Ans: b
Sol:
- Given that the manufacturer of a table sells it to the whole sale dealer at a profit of 10%
- Then the whole sale dealer sells to a retailer at a profit of 30%
- The retailer sells to a customer at a profit of 50%
- If the customer pays Rs.4290 for the table then 1.1 × 1.3 × 1.5X = 4290
X(Manufacturing cost) = Rs. 2000
Q3: Mayank buys some candies for Rs 15 a dozen and an equal number of different candies for Rs 12 a dozen. He sells all for Rs 16.50 a dozen and makes a profit of Rs 150. How many dozens of candies did he buy altogether? [2017]
(a) 50
(b) 30
(c) 25
(d) 45
Ans: a
Sol:
- Given that Mayank buys some candies for Rs.15 a dozen and equal number of different candies for Rs.12 a dozen.
- Let us assume that there are n dozens,
- Cost price of the candies = 15n + 12n = 27n
- In total he buys 2n dozens of candies.
- A dozen is sold at Rs.16.50
- Selling price of candies = 2n × 16.50 = 33n
- Profit = Selling price - Cost Price
- Profit = 33n - 27n = 6n = 150
- Therefore the no. of candies Mayank bought altogether is 2n = 2 × 25 = 50 dozens
|
166 videos|229 docs|95 tests
|
FAQs on Daily Practice Questions CAT Previous Year Questions with Answer PDF
| 1. What is the difference between profit and loss? |  |
| 2. How do you calculate the profit percentage? |  |
| 3. What is a discount and how is it calculated? |  |
| 4. How do you calculate the selling price if the cost price and profit percentage are given? |  |
| 5. How can you determine the cost price if the selling price and profit percentage are known? |  |