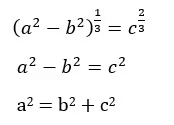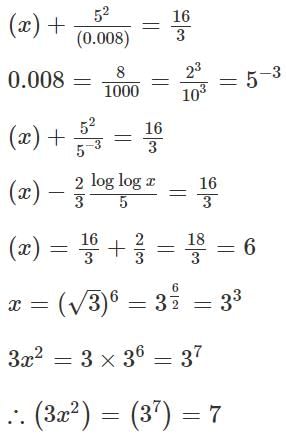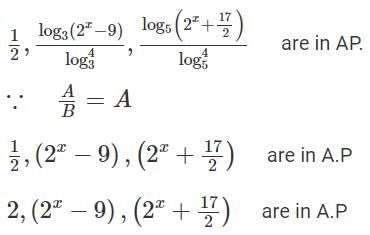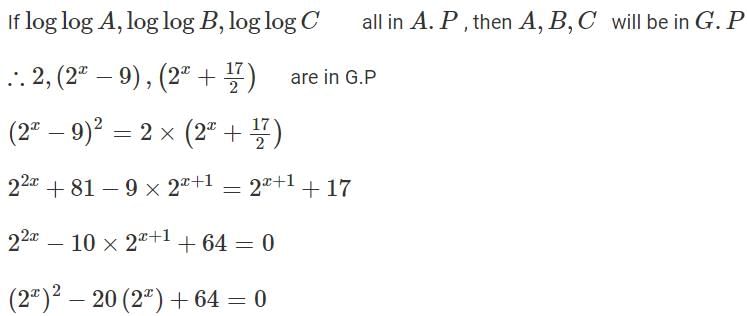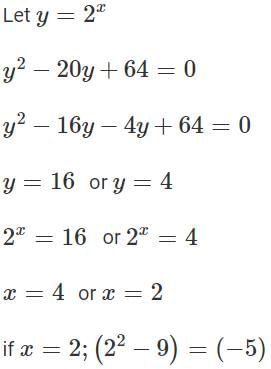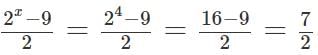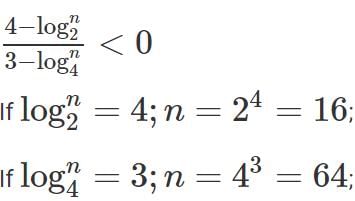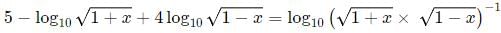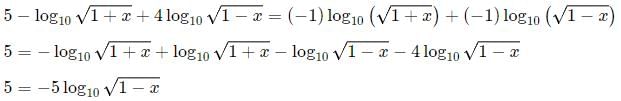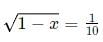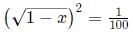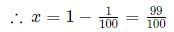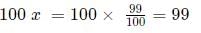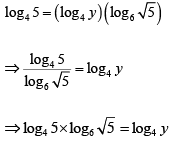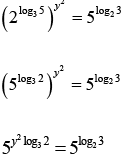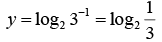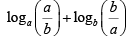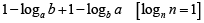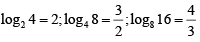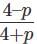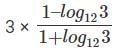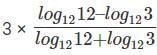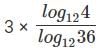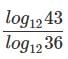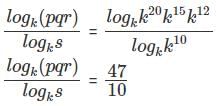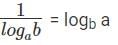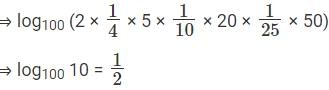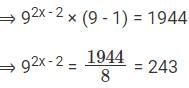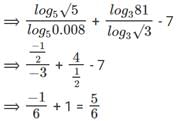Logarithms CAT Previous Year Questions with Answer PDF
2024
Q1: If x is a positive number such that 4 log10x + 4 log100x + 8 log1000x = 13, then the greatest integer not exceeding x, is
Ans: 31
Sol:
Q2: If a, b and c are postive real numbers such that a > 10 ≥ b ≥ c and  then the greatest possible integer value of a is
then the greatest possible integer value of a is
Ans: 14
Sol:
The value of a will be maximum, when both b and c will be maximum which is equal to 10 but, in that case a2 will be equal to 200 which is not possible for the integer value of a.
So, the greatest possible value a2 = 196.
So, the greatest possible integer value of a = 14
Hence, 14 is the required answer.
Q3: If 3a = 4, 4b = 5, 5c = 6, 6d = 7, 7e = 8 and 8f = 9, then the value of the product abcdef is
Ans: 2
Sol: We have
3a = 4 => a = log3 4
4b = 5 => b = log4 5
5c = 6 => c = log5 6
6d = 7 => d = log6 7
7e = 8 => e = log7 8
8f = 9 => f = log8 9
Now, a * b * c * d * e * f = log3 4 * log4 5 * … * log8 9 = log3 9 / log3 3 = 2
Hence, 2 is the required answer.
2023
Q1: If x and y are positive real numbers such that logx (x2 + 12) = 4 and 3 logy x = 1 , then x + y equals [2023]
(a) 20
(b) 11
(c) 68
(d) 10
Ans: d
Sol: logx (x2 + 12) = 4
This means, x2 + 12 = x4
Let k = x2
k + 12 = k2
k2 – k – 12 = 0
k2 – 4k + 3k – 12 = 0k(k – 4) + 3(k – 4) = 0k = 4 or k = -3
But since k = x2, k is always non-negative.∴ k = 4
∴ x2 = 4Since x is the base of the log function, it can should always be positive.
∴ x = 2
3 logyx = 1
logyx3 = 1
x3 = y1
y = x3 = 23 = 8
∴ x + y = 2 + 8 = 10
Q2: For some positive real number  , then the value of log3 (3x2) is [2023]
, then the value of log3 (3x2) is [2023]
Ans: 7
Sol:
Q3: For a real number x, if  are in an arithmetic progression, then the common difference is [2023
are in an arithmetic progression, then the common difference is [2023
(a) log47
(b) log4(3/2)
(c) log4(7/2)
(d) log4(23/2)
Ans: c
Sol:
But, since the argument of the log can't be negative, x = 4
∴ The common ratio of the G.P is
∴ The common difference of the AP = (7/2)
Q4: The sum of all possible values of x satisfying the equation 24x2 - 22x2 + x + 16 + 22x + 30 = 0, is
(a) 3/2
(b) 5/2
(c) 1/2
(d) 3
Ans: c
Sol:
2022
Q1: The number of distinct integer values of n satisfying 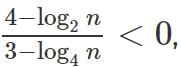 is [2022]
is [2022]
Ans: 47
Sol:
For any value of n < 16, the numerator is positive. For any value of n > 16, it is negative.For any value of n < 64, the denominator is positive. For any value of n > 64, it is negative.For a fraction to be negative, the numerator and the denominator must be of opposite signs.In this case, n should be between 16 and 64.
The number of values that n can take = 63 - 16 = 47.
Q2: If 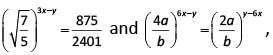 for all non-zero real values of a and b, then the value of x + y is
for all non-zero real values of a and b, then the value of x + y is
Ans: 14
Sol:
(7/5)(3x-y)/2 = 875/2401 = 125/343 = (7/5)-3
=> y – 3x = 6
(4a/b)6x-y = (b/2a)6x-y
=> But 4a/b ≠ b/2a
=> The power is 0.
=> y = 6x
=> x = 2, y = 12
x + y = 14
2021
Q1: For a real number a, if 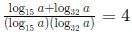 then a must lie in the range [2021]
then a must lie in the range [2021]
(a) 2 < a < 3
(b) 3 < a < 4
(c) 4 < a < 5
(d) a > 5
Ans: c
Sol:
Q2: If 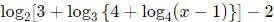 = 0 then 4x equals [2021]
= 0 then 4x equals [2021]
Ans: 5
Sol: We have :
4x = 5
Q3: If 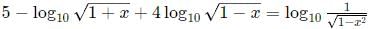 , then 100x equals [2021]
, then 100x equals [2021]
Ans: 99
Sol:
We can re-write the equation as:
Squaring both sides:
Hence,
2020
Q1: If log4 5 = log4 y log6 √5 , then y equals [2020]
Ans: 36
Sol:
⇒ y = 36
Q2: If y is a negative number such that 2y2log3 5 = 5log2 3 , then y equals [2020]
(a) log2(1 / 3)
(b) - log2(1 / 3)
(c) log2(1 / 5)
(d) - log2(1 / 5)
Ans: a
Sol: 2y2log3 5 = 5log2 3
( is negative )
Q3: The value of 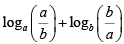 , for 1 < a ≤ b cannot be equal to [2020]
, for 1 < a ≤ b cannot be equal to [2020]
(a) -0.5
(b) 1
(c) 0
(d) -1
Ans: b
Sol:
= loga a - logab +logbb - logba
=
since ( logab + logab ) ≥ 2
∴ 1 can't be the answer.
Q4: 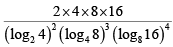 equals [2020]
equals [2020]
Ans: 24
Sol:
= 24
Q5: In the final examination, Bishnu scored 52% and Asha scored 64%. The marks obtained by Bishnu is 23 less, and that by Asha is 34 more than the marks obtained by Ramesh. The marks obtained by Geeta, who scored 84%, is [2020]
(a) 469
(b) 399
(c) 357
(d) 417
Ans: b
Sol: Let the total marks be T and scores of Bishnu, Asha and Ramesh be a, b and c respectively. Given, a = 52% of T = c - 23 and b = 64% of T = c + 34Hence, (64 - 52)% of T = (c + 34) - (c - 23) = 57i.e. 12% of T = 57
Hence, score of Geeta = 84% of T = 7 x 57 = 399
2019
Q1: Let x and y be positive real numbers such that log5(x + y) + log5(x - y) = 3, and log2y - log2x = 1 - log23. Then xy equals [2019]
(a) 25
(b) 150
(c) 250
(d) 100
Ans: b
Sol: Given that, log5(x + y) + log5(x - y) = 3We know log A + log B = log (A x B)
log5(x + y) + log5(x - y) = log5(x2 - y2)
log5(x2 - y2) = 3
x2 - y2 = 53
x2 - y2 = 125
Similarly, log2y - log2x = 1 - log23
log2 (y/x) = log22 - log23
log2(y/x) = log2(2/3)3y = 2x
(3/2)y2 - y2 = 125
(9/4)y2 - y2 = 125
5/4 y2 = 125
y2 = 100y = 10x = 15So, xy = 15 x 10 = 150
Q2: If x is a real number ,then 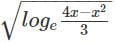 is a real number if and only if [2019]
is a real number if and only if [2019]
(a) -3 ≤ x ≤ 3
(b) 1 ≤ x ≤ 2
(c) 1 ≤ x ≤ 3
(d) -1 ≤ x ≤ 3
Ans: c
Sol: It is given that,
is a real number
Therefore,≥ 0
≥ 1
4x - x2 ≥ 3
x2 - 4x + 3 ≤ 0(x−1) (x-3) ≤ 0x ∈ [1,3]
Q3: The real root of the equation 26x + 23x+2 - 21 = 0 is [2019]
(a) 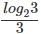
(b) log29
(c) 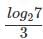
(d) log227
Ans: a
Sol: Given equation - 26x + 23x+2 - 21 = 0The idea is to convert the above equation to a quadratic one.
So, 26x = (23x)2
Let y = 23x
Now, 26x + 23x+2 - 21 = 0 can be rewritten as + 2(3x)2+ 22.23x - 21 = 0
y2 + 4y - 21 = 0Solving the above quadratic equation,(y + 7) (y - 3) = 0So, y = -7 or +3
y = 23x ⇒ y should always be positiveTherefore, y = -7 is not a valid solution. So, only y = +3 exists.
23x = 3Taking log on both sides,
log2 23x = log2 3
3x = log2 3
x = 1/3 log2 3, which is the real solution to the given equation
2018
Q1: If x is a positive quantity such that 2x = 3log52 , then x is equal to [2018]
(a) log59
(b) 1 + log5(3/5)
(c) 1 + log3 (5/3)
(d) log58
Ans: b
Sol: Given, 2x = 3log52Taking log on both sides, we get
log (2x) = log (3log52)
x × log(2) = log5(2) × log(3)Let us consider the base as 3,
Going through the options, Simplifying (B)
1 + log5 (3/5)
1 + log5(3) - log5(5)
1 + log5(3) – 1
log5(3)
Q2: If log2(5 + log3a) = 3 and log5(4a + 12 + log2b) = 3, then a + b is equal to [2018]
(a) 32
(b) 59
(c) 67
(d) 40
Ans: b
Sol: We know that if logqp = r then p = qr
Given log2(5 + log3a) = 3
5 + log3a = 23
log3a = 3
a = 33 = 27
Similarly, 4a + 12 + log2b = 53
4a + log2b = 113
log2b = 5
b = 25 = 32
a + b = 27 + 32 = 59
Q3: If log1281 = p, then  is equal to: [2018]
is equal to: [2018]
(a) log28
(b) log68
(c) log416
(d) log616
Ans: b
Sol: Given, log1281 = p
log12(3)4 = p
4 (log12(3)) = p
log12(3) = p/4 ...(1)
We need to find the value of 3 ×
This can be rewritten as 3 ×Replacing (2) with (1), We get
log3664
log68
Hence, the answer is log68
Q4: If p3 = q4 = r5 = s6, then the value of logs (pqr) is equal to [2018]
(a) 24/5
(b) 1
(c) 47/10
(d) 16/5
Ans: c
Sol: Given that p3 = q4 = r5 = s6
We have to find the value of logs (pqr)Since more variables are given, to avoid confusion assume a new variable to simplify it.
Let us assume this p3 = q4 = r5 = s6 is equal to kxso that we can get every values in k
We can rewrite this logs (pqr) asNow let us take the LCM of 3 , 4 , 5 and 6 which is equal to 60
Hence p3 = q4 = r5 = s6 = k60
Or p = k20 q = k15 r = k12 s = k10
The question is "If p3 = q4 = r5 = s6, then the value of logs (pqr) is equal to" Hence, the answer is 47/10
Q5: 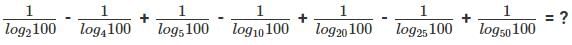 [2018]
[2018]
(a) 0
(b) 1/2
(c) -4
(d) 10
Ans: b
Sol: We know that
⇒log100 2 - log100 4 + log100 5 - log100 10 + log100 20 - log100 25 + log100 50
We also know that (- loga b) = loga (1/b)
2017
Q1: Suppose, log3x = log12y = a, where x, y are positive numbers. If G is the geometric mean of x and y, and log6G is equal to: [2017]
(a) √a
(b) 2a
(c) a/2
(d) a
Ans: d
Sol: log3 x = log12 y = a, where x, y are positive numbers.
log3 x = a; x = 3a
log12 y = a; y = 12a
If G is the geometric mean of x and y, log6G is equal to has to be foundWe know that geometric mean is √xy
√xy = √(36a)
= √(62a) = (62a)1/2
= 6a
log6 G = a
Q2: If 92x – 1 – 81x-1 = 1944, then x is [2017]
(a) 3
(b) 9/4
(c) 4/9
(d) 1/3
Ans: b
Sol: We have to find the value of x
⇒ 92x – 1 – 81x-1 = 1944
⇒ 92x – 1 – (92)x-1 = 1944
⇒ 92x – 1 – 92x - 2 = 1944
⇒ (92x - 2 × 9) - 92x - 2 = 1944
We can write 243 = 35 = 9(5/2)Comparing the powers,⇒ 2x – 2 = 5/2⇒ 2x = 9/2⇒ x = 9/4
Q3: If x is a real number such that log35 = log5(2 + x), then which of the following is true? [2017]
(a) 0 < x < 3
(b) 23 < x < 30
(c) x > 30
(d) 3 < x < 23
Ans: d
Sol: log3 5 = log5 (2 + x)
Since log3 3 = 1 and log3 9 = 2 , we can say that 2 > log3 5 > 1We need to find the range of x
If log5 (2 + x) > 1⇒ 2 + x > 5⇒ x > 3
If log5 (2 + x) < 2
⇒ 2 + x < 52⇒ 2 + x < 25⇒ x < 23
Therefore 3 < x < 23
Q4: If log(2a × 3b × 5c) is the arithmetic mean of log(22 × 33 × 5), log(26 × 3 × 57), and log(2 × 32 × 54), then a equals [TITA 2017]
Ans: 3
Sol: 3log(2a × 3b × 5c) = log(22 × 33 × 5) + log(26 × 3 × 57) + log(2 × 32 × 54)We have to find only the value of a
23a × 33b × 53c = (22 × 26 × 21) × (33 × 3 × 32) × (5 × 57 × 54)
23a = 293a = 9a = 3
Q5: The value of log0.008√5 + log√381 – 7 is equal to: [2017]
(a) 1/3
(b) 2/3
(c) 5/6
(d) 7/6
Ans: c
Sol: Here we have to find the value of log0.008 √5 + log√3 81 – 7.
⟹ log0.008 √5 + log√3 81 – 7
log0.008 √5 can be written in the terms of five and log√3 81 can be written in the terms of 3.
where √5 = 51/2 ⟹ 0.008 = 23/103 = 5-3
⟹ log0.008 √5 + log√3 81 – 7
Hence the value of log0.008√5 + log√381 – 7 = 5/6
Q6: If 9x - (1/2) – 22x – 2 = 4x – 32x – 3, then x is [2017]
(a) 3/2
(b) 2/5
(c) 3/4
(d) 4/9
Ans: a
Sol: Given that
⇒ 32x × 8 = 22x × 27
⇒ 32x - 3 = 22x - 3⇒ 2x - 3 = 0⇒ x = 3/2
|
167 videos|229 docs|95 tests
|
FAQs on Logarithms CAT Previous Year Questions with Answer PDF
| 1. What is the basic definition of logarithms? |  |
| 2. How are logarithms used in real-life applications? |  |
| 3. How do you solve logarithmic equations? |  |
| 4. What are the properties of logarithms? |  |
| 5. Can logarithms be negative? |  |