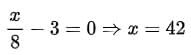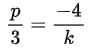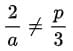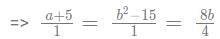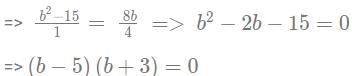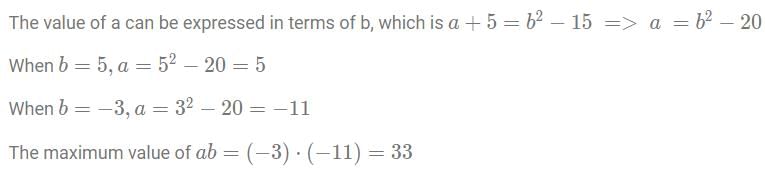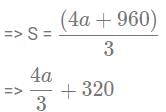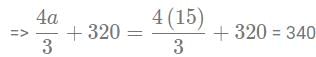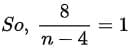Linear Equations CAT Previous Year Questions with Answer PDF
2024
Q1: A shop wants to sell a certain quantity (in kg) of grains. It sells half the quantity and an additional 3 kg of these grains to the first customer. Then, it sells half of the remaining quantity and an additional 3 kg of these grains to the second customer. Finally, when the shop sells half of the remaining quantity and an additional 3 kg of these grains to the third customer, there are no grains left. The initial quantity, in kg, of grains is
(a) 42
(b) 18
(c) 36
(d) 50
Ans: A
Sol: Let the initial quantity of grains be x. The first customer buys half of x plus 3 kg, leaving (x/2) - 3 kg. The second customer then buys half of the remaining grains plus 3 kg, leaving (x/2) - 3 kg. The third customer buys half of what is left plus 3 kg, leaving 0 grains. Thus, we have the equation:
Q2: If x and y satisfy the equations |x| + x + y = 15 and x + |y| = 20, then (x - y) equals
(a) 5
(b) 10
(c) 20
(d) 15
Ans: (b)
Sol:
We are given the following two equations:
|x| + x + y = 15 (Equation 1)
x + |y| = 20 (Equation 2)
We need to consider different cases based on the values of x and y.Case 1: x ≥ 0
If x ≥ 0, then |x| = x. Substituting this into Equation 1:
x + x + y = 15
2x + y = 15 (Equation 3)
From Equation 2, since x ≥ 0, we have |y| = y (assuming y ≥ 0):
x + y = 20 (Equation 4)
Now, we have the system of two equations:
1. 2x + y = 15
2. x + y = 20
Step 1: Solve the system of equations
Subtract Equation 2 from Equation 1:
(2x + y) - (x + y) = 15 - 20
x = -5
Substitute x = -5 into Equation 2:
-5 + y = 20
y = 25
Thus, for x = -5 and y = 25, we have:
x - y = -5 - 25 = -30
Case 2: x < 0
If x < 0, then |x| = -x. Substituting this into Equation 1:
−x + x + y = 15
y = 15 (Equation 5)
Now substitute y = 15 into Equation 2:
x + |y| = 20
Since y = 15, we have |y| = 15. Thus:
x + 15 = 20
x = 5
Thus, for x = 5 and y = 15, we have:
x - y = 5 - 15 = -10
Final Answer: Based on these calculations, the correct answer is 10.
Q3: For some constant real numbers p, k and a, consider the following system of linear equations in x and y:
px - 4y = 2 (1)
3x + ky = a (2)
A necessary condition for the system to have no solution for (x, y) is:
(a) p - 6 = 0
(b) kp + 12 ≠ 0
(c) p + 6 = 0
(d) 2a + k ≠ 0
Ans: (d) 2a + k ≠ 0
Sol: For the system of linear equations to have no solution, the lines represented by the equations must be parallel but not coincident. This can be determined using the condition for parallelism of two lines:For the system:
px - 4y = 2 (Equation 1)
3x + ky = a (Equation 2)
A necessary condition for parallelism that the coefficients of x and y in both equations must be proportional:This simplifies to:
p - k = -12 (Equation 1)
For the system to have no solution, the constant terms must not be in the same proportion. Therefore, we have the condition:
This gives the relationship:
2023
Q1: For some real numbers a and b, the system of equations x + y = 4 and (a + 5) x + (b2 - 15) y = 8b has infinitely many solutions for x and y. Then, the maximum possible value of ab is
(a) 33
(b) 25
(c) 15
(d) 55
Ans: a
Sol: It is given that for some real numbers a and b, the system of equations x + y = 4 and (a+5)x + (b2 - 15)y = 8b has infinitely many solutions for x and y.
Hence, we can say that
This equation can be used to find the value of a, and b.Firstly, we will determine the value of b.
Hence, the values of b are 5, and -3, respectively.
Q2: A fruit seller has a stock of mangoes, bananas and apples with at least one fruit of each type. At the beginning of a day, the number of mangoes make up 40% of his stock. That day, he sells half of the mangoes, 96 bananas and 40% of the apples. At the end of the day, he ends up selling 50% of the fruits. The smallest possible total number of fruits in the stock at the beginning of the day is
Ans: 340
Sol: Let us assume the initial stock of all the fruits is S.
Let us take we have 'b' and 'a' mangoes initially.
Stock of Mangoes = 40% of S = 2S/5
The total number of fruits sold are Mangoes Sold + Apples Sold + Bananas Sold
= 2S/10 + 96 + 4a/10 = S/2 (Given)
=> S/5 + 96 + 2a/5 = S/2
'a' has to be a multiple of 3 for the above term to be an integer.
But 'a' has to be a multiple of 5 for 4a/10 to be an integer.
=> The smallest value of 'a' satisfying both conditions is 15.
2022
Q1: If 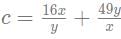 for some non-zero real numbers x and y, then c cannot take the value
for some non-zero real numbers x and y, then c cannot take the value
(a) 60
(b) -50
(c) -70
(d) -60
Ans: b
Sol:
As -50 is not in the range of b so it is the answer
2019
Q1: Let A be a real number. Then the roots of the equation x2 - 4x - log2A = 0 are real and distinct if and only if [2019]
(a) A < 1/16
(b) A > 1/8
(c) A > 1/16
(d) A < 1/8
Ans: C
Sol: For roots of any quadratic equation to be real and distinct, D > 0.
So, for x2 − 4x − log₂A = 0,
D = (−4)2 − 4 × 1 × (−log2A) > 0
16 + 4 log2A > 0
4 + log2A > 0
log2A > −4
A > 1/24
A > 1/16
Q2: The quadratic equation x2 + bx + c = 0 has two roots 4a and 3a, where a is an integer. Which of the following is a possible value of b² + c?
(a) 3721
(b) 549
(c) 361
(d) 427
Ans: B
Sol: Given quadratic equation is x2 + bx + c = 0
Sum of roots = -b → -b = 4a + 3a = 7a
Product of roots = c → c = 4a × 3a = 12a²
b2 = 49a2 and c = 12a2
b2 + c = 49a² + 12a2 = 61a2
Our answer must be a multiple of 61 and a perfect square
549 = 61 × 9 = 61 × 32
Thus, possible value of b2 + c = 549
Q3: What is the largest positive integer 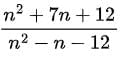 such that is also positive integer?
such that is also positive integer?
(a) 6
(b) 8
(c) 16
(d) 12
Ans: D
Sol:
n cannot be -3
has to be an integer
The value has to be equal to 1 for n to be high
n = 12
if we put n=16
then 8/(n-4) won’t be a integer
|
2 videos|84 docs|456 tests
|
FAQs on Linear Equations CAT Previous Year Questions with Answer PDF
| 1. What are linear equations? |  |
| 2. How do you solve a system of linear equations? |  |
| 3. What is the importance of linear equations in real life? |  |
| 4. Can a linear equation have multiple solutions? |  |
| 5. How do you know if a system of linear equations has no solution? |  |