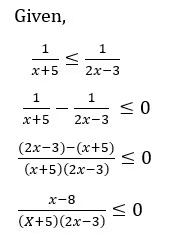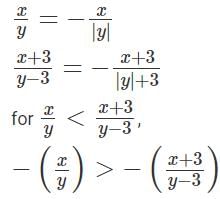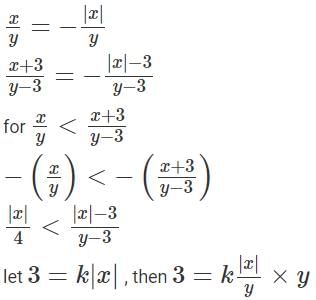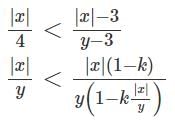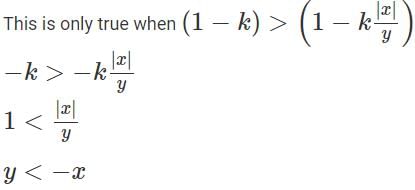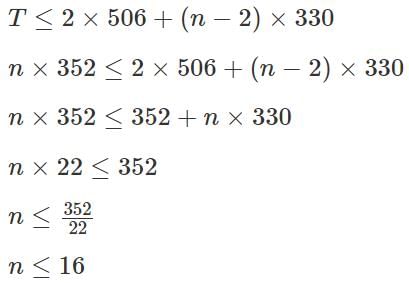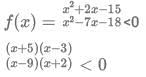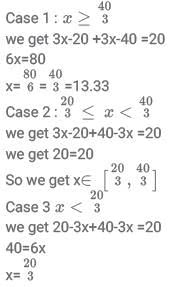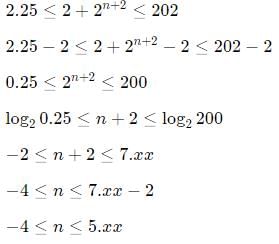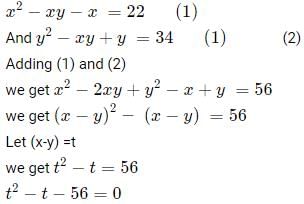Inequalities CAT Previous Year Questions with Answer PDF
2024
Q1: The value of x satisfying the inequality 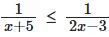 are
are
(a) -5 < x < 3/2 or 3/2 < x ≤ 8
(b) x < -5 or x > 3/2
(c) x < -5 or 3/2 < x ≤ 8
(d) -5 < x < 3/2 or x > 3/2
Ans: (c)
Sol:
So, for the given inequality to hold true x < –5 or 3/2 < x ≤ 8
Hence, option C is the required answer.
Q2: The number of distinct real values of x, satisfying the equation
max{x, 2} - min{x, 2} = |x + 2| - |x - 2|, is
Ans: 2
Sol: We have,
max{x, 2} – min{x, 2} = |x + 2| – |x – 2|
Case1–> For x ≥ 2
x – 2 = x + 2 – (x – 2)
x – 2 = 4
x = 6
Thus for x ≥ 2, x = 6 is a solution.
Case 2–> For x < 2
2 – x = (x + 2) – (2 – x)
2 – x = 2x
x = 2/3
Hence, 2 distinct values of x exist.
2023
Q1: Any non-zero real numbers x, y such that y ≠ 3 and x/y < 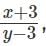 will satisfy the condition [2023]
will satisfy the condition [2023]
(a) If y > 10 , then −x > y
(b) If x < 0, then −x < y
(c) If y < 0, then −x < y
(d) 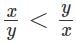
Ans: c
Sol: Case I)
If both x and y are both positive.
Then,is always true, since We are increasing the numerator and decreasing the denominator.
Case II)
If both x and y are both negative.
Case III)
x is positive and y is negative.This is always true since we are increasing the numerator and decreasing the denominator.
Case IV)
x is negative and y is positive.
Observe that k is always positive.
So, the given condition holds good when both x & y are positive or x is positive but y is negative or x is negative, y is positive and y < −x Since y is negative in the third option, −x < y , implies that x > |y|, that is x is positive.
We know that when y is negative and x is positive the condition always holds good.
Q2: If a certain amount of money is divided equally among n persons, each one receives Rs 352. However, if two persons receive Rs 506 each and the remaining amount is divided equally among the other persons, each of them receive less than or equal to Rs 330. Then, the maximum possible value of n is [2023]
Ans: 16
Sol: Let the total amount be equal to T.
T = n × 352
“However, if two persons receive Rs 506 each and the remaining amount is divided equally among the other persons, each of them receive less than or equal to Rs 330”
So, the maximum value that n can take is 16.
Q3: Let n and m be two positive integers such that there are exactly 41 integers greater than 8m and less than 8n (m<n), which can be expressed as powers of 2. Then, the smallest possible value of n + m is [2023]
(a) 14
(b) 42
(c) 16
(d) 44
Ans: c
Sol:
It is given that there are exactly 41 numbers, which can be expressed as the power of two, and exist between 8m and 8n, (where m, and n are positive integers, and m < n)
Hence, 23m < 41 numbers < 23n
Since, m is a positive integer, the least value of m is 1. Therefore, 23m = 23, hence, the 41 numbers between them are:
24, 25, 26, ..., 244
Then the lowest possible value of 8n is 245. Hence, the smallest value of n is:
245 = 8n ⇒ 23n = 245 ⇒ n = 15
Hence, the smallest value of m + n is (15 + 1) = 16
2022
Q1: The largest real value of a for which the equation |X + a| + |x − 1| = 2 has an infinite number of solutions for x is
(a) 0
(b) 2
(c) 1
(d) -1
Ans: c
Sol: In the question, it is given that the equation ∣x + a∣ + ∣x − 1∣ = 2 has an infinite number of solutions for any value of x. This is possible when x in |x+a| and x in |x-1| cancels out.
Case 1:
x + a < 0, x - 1 ≥ 0
- a - x + x - 1 = 2
a = -3
Case 2:
x + a ≥ 0 and x - 1 < 0
x + a - x + 1 = 2
a = 1
Largest value of a is 1.
Q2: If 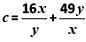 for some non-zero real numbers x and y, then c cannot take the value
for some non-zero real numbers x and y, then c cannot take the value
(a) 60
(b) -50
(c) -70
(d) -60
Ans: b
Sol:
Use AM ≥ GM
=> c/2 ≥ √(16x/y * 49y/x)
=> c ≥ 56
Since x and y are non-zero real numbers, they can be -ve as well. So, we will also get c ≤ -56
Hence, -50 cannot be the value of c.
Q3: The minimum possible value of 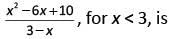
(a) -2
(b) -(1/2)
(c) 1/2
(d) 2
Ans: d
Sol:
[(3 – x)2 + 1]/(3 – x) = (3 – x) + 1/(3 – x)
Since x < 3, 3 – x will always be +ve.
And we know that a + 1/a ≥ 2 if a > 0
So, min value = 2
2021
Q1: For natural numbers x, y, and z, if xy + yz = 19 and yz + xz = 51, then the minimum possible value of xyz is [2022]
Ans: 34
Sol: It is given, y(x + z) = 19
y cannot be 19.
If y = 19, x + z = 1 which is not possible when both x and z are natural numbers.
Therefore, y = 1 and x + z = 19
It is given, z(x + y) = 51
z can take values 3 and 17
Case 1:
If z = 3, y = 1 and x = 16
xyz = 3*1*16 = 48
Case 2:
If z = 17, y = 1 and x = 2
xyz = 17*1*2 = 34
Minimum value xyz can take is 34.
Q2:  is negative if and only if
is negative if and only if
(a) -5 < x < -2 or 3 < x < 9
(b) x < -5 or -2 < x < 3
(c) -2 < x < 3 or x > 9
(d) x < -5 or 3 < x < 9
Ans: a
Sol:We have four inflection points -5, -2, 3, and 9.
For x<-5, all four terms (x+5), (x-3), (x-9), (x+2) will be negative. Hence, the overall expression will be positive. Similarly, when x>9, all four terms will be positive.
When x belongs to (-2,3), two terms are negative and two are positive. Hence, the overall expression is positive again.
We are left with the range (-5,-2) and (3,9) where the expression will be negative.
Q3: For a real number x the condition 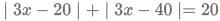 necessarily holds if
necessarily holds if
(a) 10 < x < 15
(b) 9 < x < 14
(c) 7 < x < 12
(d) 6 < x < 11
Ans: c
Sol:but this is not possible
so we get from case 1,2 and 3Now looking at options
we can say only option C satisfies for all x .
Hence 7<x<12.
Q4: The number of integers n that satisfy the inequalities ∣n−60∣ < ∣n−100∣ <∣n−20∣ is [2021]
(a) 21
(b) 19
(c) 18
(d) 20
Ans: b
Sol: We have ∣n−60∣ < ∣n−100∣ <∣n−20∣
Now, the difference inside the modulus signified the distance of n from 60, 100, and 20 on the number line. This means that when the absolute difference from a number is larger, n would be further away from that number.
Example: The absolute difference of n and 60 is less than that of the absolute difference between n and 20. Hence, n cannot be ≤ 40, as then it would be closer to 20 than 60, and closer on the number line would indicate lesser value of absolute difference. Thus we have the condition that n > 40.
The absolute difference of n and 100 is less than that of the absolute difference between n and 20. Hence, n cannot be ≤ 60, as then it would be closer to 20 than 100. Thus we have the condition that n > 60.
The absolute difference of n and 60 is less than that of the absolute difference between n and 100. Hence, n cannot be \ge80≥80, as then it would be closer to 100 than 60. Thus we have the condition that n<80.
The number which satisfies the conditions are 61, 62, 63, 64......79.
Thus, a total of 19 numbers.
Q5: For all possible integers n satisfying 2.25 ≤ 2 + 2n+2 ≤ 202, then the number of integer values of 3 + 3n+1 is: [2021]
Ans: 7
Sol:
Possible integers = -4, -3, -2, -1, 0, 1, 2, 3, 4, 5
If we see the second expression that is provided, i.e
3 + 3n+1, it can be implied that n should be at least -1 for this expression to be an integer.
So, n = -1, 0, 1, 2, 3, 4, 5.
Hence, there are a total of 7 values.
Q6: Consider the pair of equations: x2 − xy − x = 22 and y2 − xy + y = 34. If x > yx > y, then x - yx − y equals [2021]
(a) 6
(b) 4
(c) 7
(d) 8
Ans: d
Sol: We have,
(t - 8)(t + 7) = 0
so t = 8
so x - y = 8
Q7: The number of distinct pairs of integers (m,n), satisfying ∣1+mn∣ < ∣m+n∣ < 5 is: [2021]
Ans: 12
Sol: Let us break this up into 2 inequations [ Let us assume x as m and y as n ]
| 1 + mn | < | m + n |
| m + n | < 5
Looking at these expressions, we can clearly tell that the graphs will be symmetrical about the origin.
Let us try out with the first quadrant and extend the results to the other quadrants.
We will also consider the +X and +Y axes along with the quadrant.
So, the first inequality becomes,
1 + mn < m + n
1 + mn - m - n < 0
1 - m + mn - n < 0
(1-m) + n(m-1) < 0
(1-m)(1-n) < 0
(m - 1)(n - 1) < 0
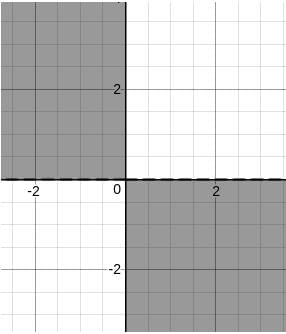
Let us try to plot the graph.
If we consider only mn < 0, then we get
But, we have (m - 1)(n - 1) < 0, so we need to shift the graphs by one unit towards positive x and positive y.
So, we have,
But, we are only considering the first quadrant and the +X and +Y axes. Hence, if we extend, we get the following region.
So, if we look for only integer values, we get
(0,2), (0,3),.......
(0,-2), (0, -3),......
(2,0), (3,0), ......
(-2,0), (-3,0), .......
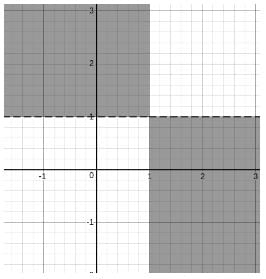
Now, let us consider the other inequation as well, in which |x + y| < 5
Since one of the values is always zero, the modulus of the other value is less than or equal to 4.
Hence, we get
(0,2), (0,3), (0,4)
(0,-2), (0, -3), (0, -4)
(2,0), (3,0), (4,0)
(-2,0), (-3,0), (-4,0)
Hence, a total of 12 values.
2018
Q1: The smallest integer n for which 4n > 1719 holds, is closest to [2018]
(a) 33
(b) 39
(c) 37
(d) 35
Ans: b
Sol: According to Question, 4n > 1719
⇒ (161/2)n > 1719
⇒ 16n/2 > 1719
Therefore, we can say that n/2 > 19
⇒ n > 38
As we have been asked about the smallest integer value of n
∴ n = 39
Q2: The smallest integer n such that n3 - 11n2 + 32n - 28 > 0 is (TITA 2018)
Ans: 8
Sol: Given, n3 – 11n2 + 32n – 28 > 0
⇒ (n - 2)(n2 – 9n + 14) > 0
⇒ (n - 2)(n - 7)(n - 2) > 0
⇒ For n < 2, (n – 2)(n – 7)(n – 2) is negative.
⇒ For 2 < n < 7, (n – 2)(n – 7)(n – 2) is negative.
⇒ For n > 7, (n – 2)(n – 7)(n – 2) is positive.
When n = 8, (n – 2)(n – 7)(n – 2) = 36, which is greater than 0.
The least integral value of n which satisfies the inequation is 8.
Q3: If a and b are integers such that 2x2 − ax + 2 > 0 and x2 − bx + 8 ≥ 0 for all real numbers x, then the largest possible value of 2a − 6b is (TITA 2018)
Ans: 36
Sol: When any quadratic equation is greater than 0 then D(Discriminant) will be less than 0.
Calculation:
⇒ 2x2 – ax + 2 > 0; Where x belongs to R
As, 2x2 – ax + 2 > 0
∴ D < 0
⇒ b2 – 4ac < 0
⇒ a2 – 4 × 2 × 2 < 0
⇒ a2 < 16 -4 < a < 4
Now, x2 − bx + 8 ≥ 0; Where x belongs to R
∴ D ≤ 0 ⇒ b2 – 4ac ≤ 0
⇒ b2 – 4 × 1 × 8 ≤ 0
⇒ b2 ≤ 32 -4√2 ≤ b ≤ 4√2
As b is an integer, -5 ≤ b ≤ 5
We have been asked about the maximum possible value of 2a – 6b
Therefore, We will take a = 3 and b = -5 to get the maximum value.
Hence, maximum possible value of 2a – 6b = 2(3) – 6(–5) = 36
2017
Q1: For how many integers n, will the inequality (n – 5) (n – 10) – 3(n – 2) ≤ 0 be satisfied? (TITA 2017)
Ans: 11
Sol: ⇒ (n - 5) (n - 10) - 3 × (n - 2) ≤ 0
⇒ n2 - 15n + 50 - 3n + 6 ≤ 0
⇒ n2 - 18n + 56 ≤ 0
⇒ (n - 14) (n - 4) ≤ 0
⇒ 4 ≤ n ≤ 14, n = {4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}
⇒ Total integer is 11
∴ The required result will be 11.
|
167 videos|229 docs|95 tests
|
FAQs on Inequalities CAT Previous Year Questions with Answer PDF
| 1. What are the types of inequalities commonly tested in the CAT exam? |  |
| 2. How can I solve inequalities algebraically during the CAT exam? |  |
| 3. Can graphical methods be used to solve inequalities in the CAT exam? |  |
| 4. How can I practice inequalities for the CAT exam? |  |
| 5. Are inequalities an important topic for the CAT exam? |  |